目錄

1444. 切披薩的方案數

題目描述：

實現代碼與解析：

二維后綴和? + 動態規劃

原理思路：

---

1444. 切披薩的方案數

題目描述：

????????給你一個?rows x cols?大小的矩形披薩和一個整數?k?，矩形包含兩種字符：?'A'?（表示蘋果）和?'.'?（表示空白格子）。你需要切披薩?k-1?次，得到?k?塊披薩并送給別人。

切披薩的每一刀，先要選擇是向垂直還是水平方向切，再在矩形的邊界上選一個切的位置，將披薩一分為二。如果垂直地切披薩，那么需要把左邊的部分送給一個人，如果水平地切，那么需要把上面的部分送給一個人。在切完最后一刀后，需要把剩下來的一塊送給最后一個人。

請你返回確保每一塊披薩包含?至少?一個蘋果的切披薩方案數。由于答案可能是個很大的數字，請你返回它對 10^9 + 7 取余的結果。

示例 1：

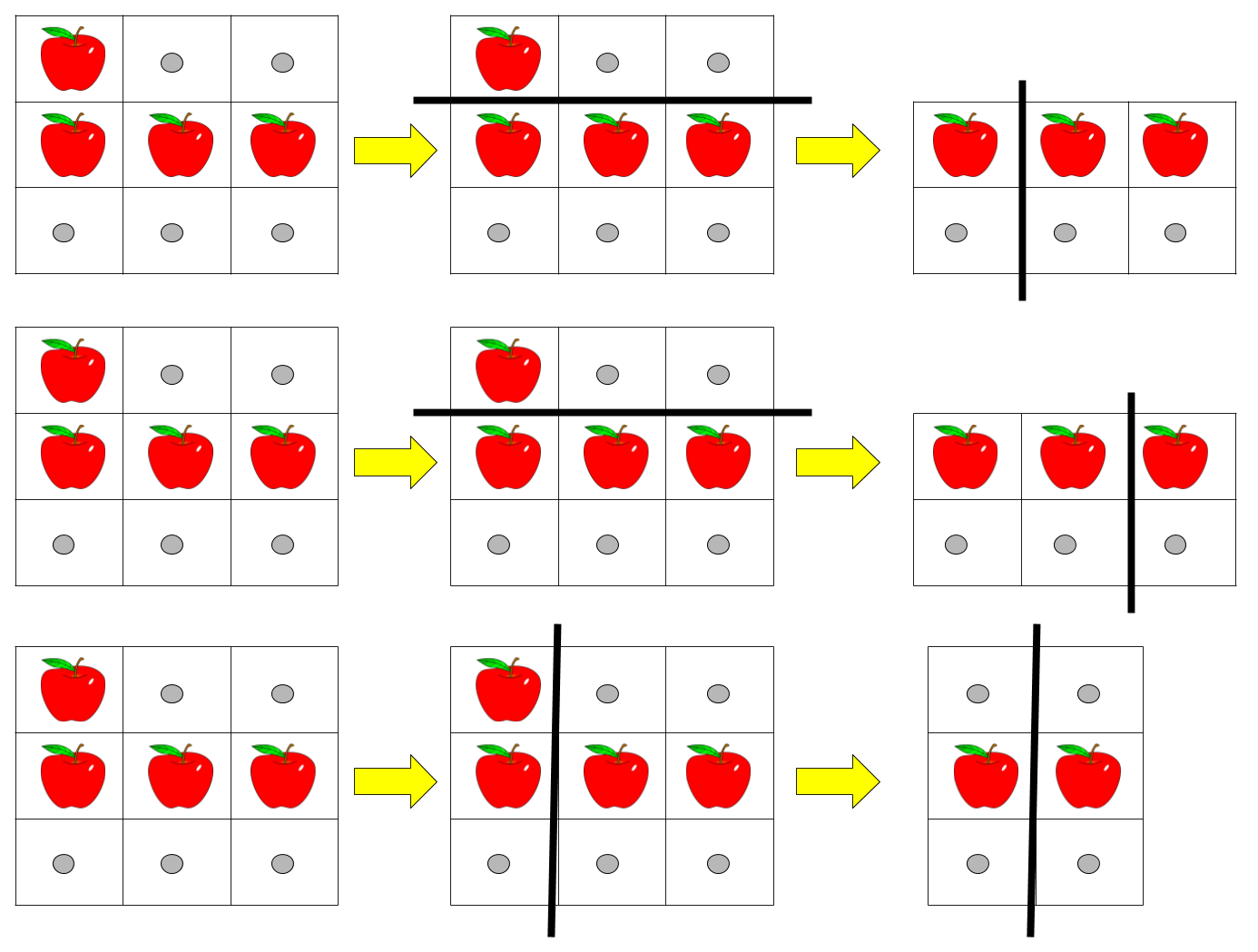
輸入：pizza = ["A..","AAA","..."], k = 3
輸出：3 
解釋：上圖展示了三種切披薩的方案。注意每一塊披薩都至少包含一個蘋果。

示例 2：

輸入：pizza = ["A..","AA.","..."], k = 3
輸出：1

示例 3：

輸入：pizza = ["A..","A..","..."], k = 1
輸出：1

提示：

• 1 <= rows, cols <= 50
• rows ==?pizza.length
• cols ==?pizza[i].length
• 1 <= k <= 10
• pizza?只包含字符?'A'?和?'.'?。

實現代碼與解析：

二維后綴和? + 動態規劃

class Solution {
public:int ways(vector<string>& pizza, int k) {int m = pizza.size(), n = pizza[0].size(), mod = 1e9 + 7;vector<vector<vector<int>>> f(k, vector<vector<int>>(m, vector<int>(n)));vector<vector<int>> apples(m + 1, vector<int>(n + 1)); // 后綴和// 后綴和 與 初始化dp數組for (int i = m - 1; i >= 0; i--){for (int j = n - 1; j >= 0; j--){apples[i][j] = apples[i + 1][j] + apples[i][j + 1] - apples[i + 1][j + 1] + (pizza[i][j] == 'A');f[0][i][j] = apples[i][j] > 0;}} for (int kk = 1; kk < k; kk++){for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){// 選擇此刀的切割位置// 水平切, 遍歷切的位置for (int a = i + 1; a < m; a++){// 上面的一塊中至少要有一個蘋果if (apples[i][j] > apples[a][j]){f[kk][i][j] = (f[kk][i][j] + f[kk - 1][a][j]) % mod;}}// 垂直切for (int b = j + 1; b < n; b++){// 左側塊中至少有一個蘋果if (apples[i][j] > apples[i][b]){f[kk][i][j] = (f[kk][i][j] + f[kk - 1][i][b]) % mod;}}}}}return f[k - 1][0][0];}
};

原理思路：

? ? ? ? apples 數組，后綴和用于記錄一塊披薩中的蘋果數量，用一塊中的左上角來代替此塊含有的蘋果數。

? ? ? ? 此題的關鍵是，dp[ k ][ i ][ j ] 的含義：代表還剩下 k 刀沒切，剩下的是左上角為?i ，j 的披薩狀態時的切割方案總數。這是我自己的理解，力扣上dp數組定義的含義感覺不如我這樣寫和解釋更直觀，不過原理肯定是一樣的。

? ? ? ? 知道dp數組的含義，就很好寫了。

? ? ? ? 首先計算 apples 數組，這個就不用解釋了，不會的話，建議去學習一下前綴和，二維前綴和的基礎算法就行，同時初始化一下dp。

? ? ? ? 初始化dp數組：顯然在還需要切0刀，剩下最后一塊披薩中有蘋果時，表示切好了，是一種情況，賦值為1，否則不成立賦值為0；

f[0][i][j] = apples[i][j] > 0;

? ? ? ? 遍歷順序：一定是先遍歷切割刀數，因為就比如一個形狀披薩狀態下，切兩刀肯定需要切一刀的狀態遞推而來，后面根據遞推式也能看出來。

? ? ? ? 遞推方程：兩種切法分類討論：

? ? ? ? 水平切：肯定是從第一行下邊開始切，總不能切空氣吧，所以是 i + 1 開始遍歷，然后切完后上面的那塊中一定要有蘋果，所以需要判斷一下，切完此刀后，剩下的大塊需要再切 kk - 1刀，我們就不用再去遍歷了，dp數組含義就是這個，根據這個寫出遞推式。

????????????????遞推式：f[ kk ][ i ][ j ] = (f[ kk ][ i ][ j ] + f[ kk - 1 ][ a ][ j ]) % mod;

? ? ? ? 垂直切：與水平切同理，直接給出遞推式：

? ? ? ? ? ? ? ? 遞推式：f[ kk ][ i ][ j ] = (f[ kk ][ i ][ j ] + f[ kk - 1 ][ i ][ b ]) % mod;

? ? ? ?最后，返回結果，顯然，在初始狀態還剩切k - 1刀時是我們需要的結果狀態。

???????return f[ k - 1 ][ 0 ][ 0 ];

???????結束。