2023.8.17

?

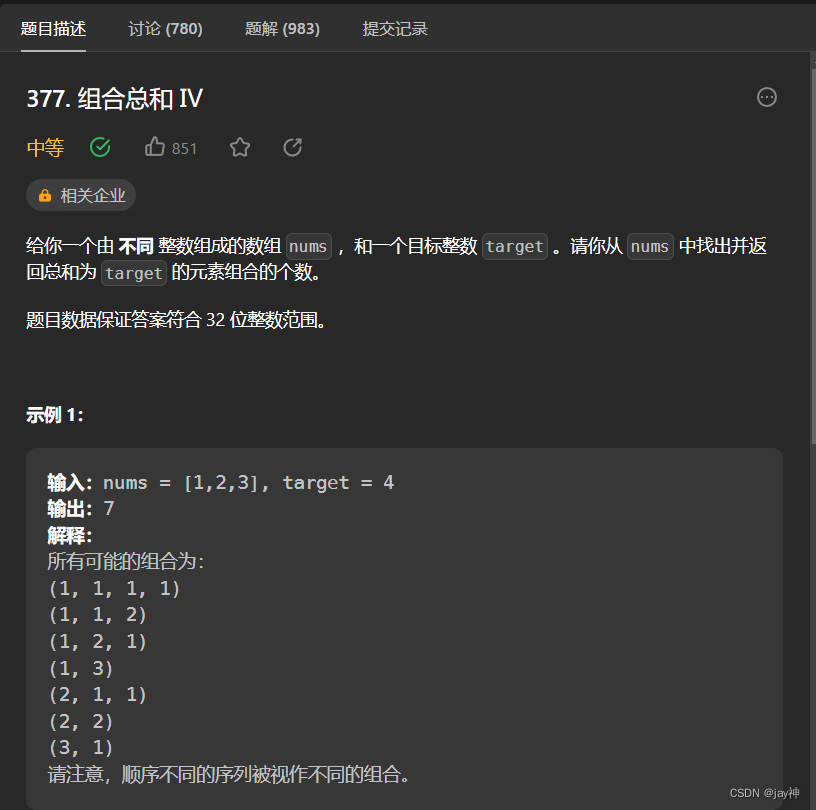
? ? ? ? ?本題屬于完全背包問題，乍一看和昨天那題?零錢兌換II?類似，但細看題目發現：今天這題是排列問題，而“零錢兌換II”是組合問題。排列問題強調順序，而組合順序不強調順序。

? ? ? ? 這里先說個結論：先遍歷物品，再遍歷背包，求出來的是組合數。(即{1，2}和{2，1}是等價的)? ? ???而先遍歷背包，再遍歷物品，求出來的是排列數。(即{1，2}和{2，1}是不等價的。)

? ? ? ? 本題思路還是和昨天那題類似，但是物品和背包的遍歷順序需要調換一下，因為本題需要求的是排列數。 代碼如下：

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<unsigned int> dp(target+1);dp[0] = 1;for(int j=0; j<=target; j++){for(int i=0; i<nums.size(); i++){if(j >= nums[i]){dp[j] += dp[j-nums[i]];}}}return dp[target];}
};

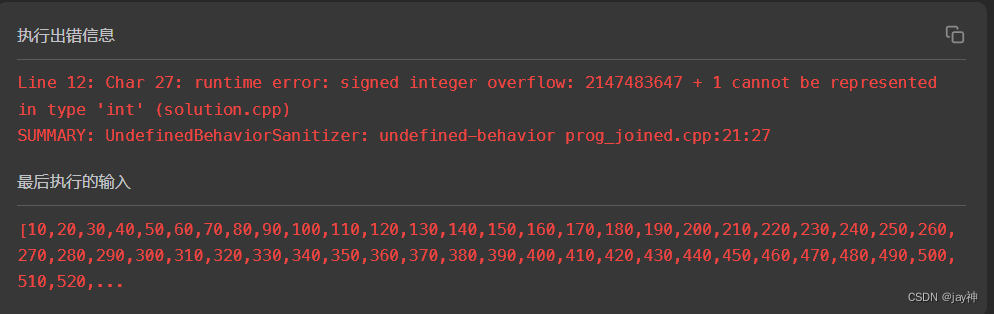
? ? ? ? ps：cpp代碼的dp數組需要聲明為<unsigned int>，不然如下示例通過不了。

?