Background
- 對于數學規劃問題,有很多的實現。Matlab+YALMIP+CPLEX這個組合應該是比較主流的,尤其是在電力相關系統中占據著比較重要的地位。
MATLAB是一個強大的數值計算工具,用于數學建模、算法開發和數據分析。Yalmip是一個MATLAB工具箱,用于建模和解決凸優化問題。它提供了一個簡單的語法,使用戶能夠輕松地定義優化問題,并使用各種內置求解器求解這些問題。Cplex是一個商業優化求解器,由IBM公司開發。它可以用于解決各種優化問題,包括線性規劃、混合整數線性規劃和二次規劃等。在MATLAB中,用戶可以使用Yalmip接口輕松地與Cplex集成。- 目前 cplex 對 python 的支持目前還不是太全,相關的學習資料比較少,ibm 自己出的資料對 python 包的介紹也很簡略,例子及相關類方法的介紹也不詳細,這一點遠沒有對 java 或 c++ 支持地好。
- 關于一些求解簡單線性規劃問題,python中也有一些庫可以實現:
z3-solver是由Microsoft Research(微軟)開發的SMT求解器,它用于檢查邏輯表達式的可滿足性,可以找到一組約束中的其中一個可行解,缺點是無法找出所有的可行解(對于規劃求解問題可以是scipy)。z3-solver可應用于軟/硬件的驗證與測試、約束求解、混合系統的分析、安全、生物,以及幾何求解等問題。Z3 主要由 C++ 開發,提供了 .NET、C、C++、Java、Python 等語言調用接口。scipy庫中的函數scipy.optimize.linprog也可以進行線性規劃求解,但不支持整數約束,只能求解出實數。pulp庫是一個專門進行規劃求解的庫。pulp庫也不是萬能的,雖然可以解決線性規劃問題,但不能進行非線性的規劃求解。當然對于規劃求解,95%以上的場景都是線性規劃求解,pulp就足夠應對我們需要應對的場景。pulp庫它將優化問題描述為數學模型,生成MPS或者LP文件,然后調用LP求解器,如CBC、GLPK、CPLEX、Gurobi等來進行求解。- 安裝完pulp庫默認就擁有了CBC求解器,其他求解器需要額外安裝才能使用,這里我沒有測試這個。
cvxpy庫是一個用于凸優化的Python庫,它提供了一個簡潔的、符合數學約束的方式來定義和求解各種凸優化問題。cvxpy的目標是提供一個易于使用的界面,使用戶能夠以簡潔的方式表達凸優化問題,并通過優化求解器快速求解。內建的凸優化問題集類:cvxpy包含了一系列常見的凸優化問題模型,如線性規劃、二次規劃、半正定規劃等。支持多種求解器:cvxpy可以與多個優化求解器集成,包括open-source的solver(如SCS、ECOS等)以及商業求解器(如Gurobi、CPLEX等)。
1、單個決策變量-scipy
- 線性規劃案例
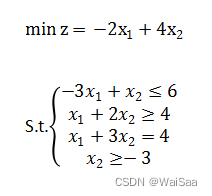
1.1、matlab+yalmip+cplex實現
%% yalmip+cplex
%(1)設定決策變量X(1)、X(2)
%(2)sdpvar:實數變量;binvar:0—1變量;intvar:整型變量
%(3)Yalmip默認是對稱的,要求非對稱用full% 清除工作區
clear;clc;close all;
% function [m1, m2]=test_cplex()
% 創建決策變量
x=sdpvar(2,1,'full');
% 添加約束條件
st=[];
st=[st,-3*x(1)+x(2)<=6];
st=[st,x(1)+2*x(2)>=4];
st=[st,x(1)+3*x(2)==4];
st=[st,x(2)>=-3];
% 配置求解器
ops = sdpsettings('solver','cplex','verbose',0);
% 目標函數,默認最小
z=-2*x(1)+4*x(2);
% 求解,如果最大值用-z
reuslt = optimize(st,z,ops);
% 求解結果x的值
x=value(x);
% 目標函數的最優解,即最小值
z=value(z);
% 打印結果
fprintf('x:%s\n', join(string(x),', '))
fprintf('z:%d\n', z)
- 運行結果
x:13, -3
z:-38
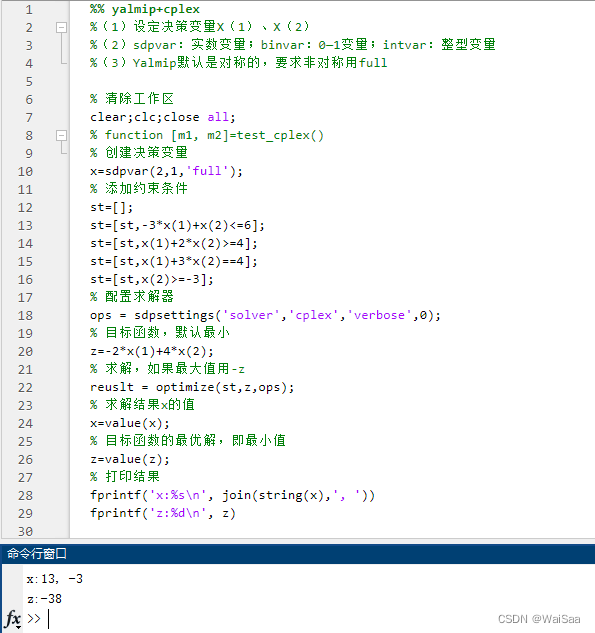
1.2、python3+scipy實現
scipy.optimize.linprog
這里只介紹后面要用到的幾個參數。
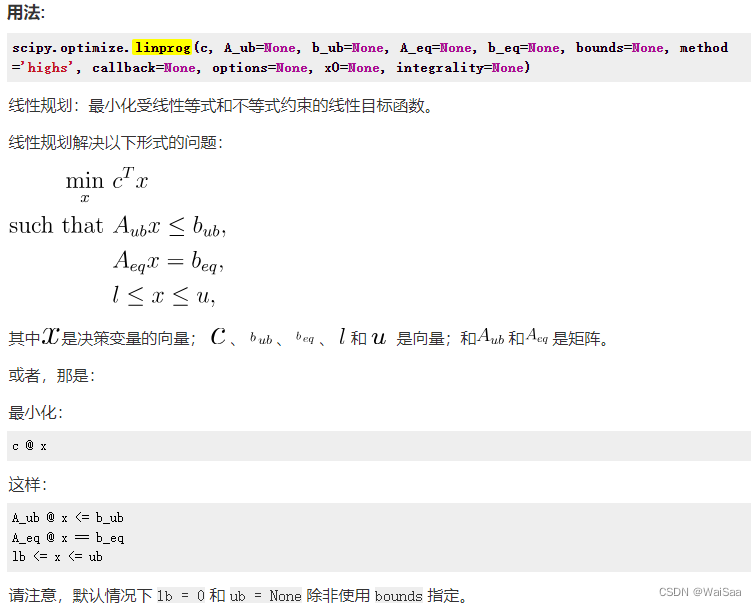

- 代碼實現
import numpy as np
from scipy.optimize import linprogdef main():"""主函數"""# 要最小化的線性目標函數的系數c = np.array([-2, 4])# 不等式約束矩陣A_ub = np.array([[-3, 1], [-1, -2]])B_ub = np.array([6, -4])# 等式約束矩陣A_ed = np.array([[1, 3]])B_ed = np.array([4])# 決策變量的最小值和最大值對序列bounds = [None, None], [-3, None]# 求解res = linprog(c, A_ub, B_ub, A_ed, B_ed, bounds=bounds)# 求解結果x的值x = list(res.x.round())# 目標函數的最優解,即最小值z = round(res.fun)print(f'x: {x}')print(f'z: {z}')print(f'msg: {res.message}')if __name__ == '__main__':main()- 運行結果
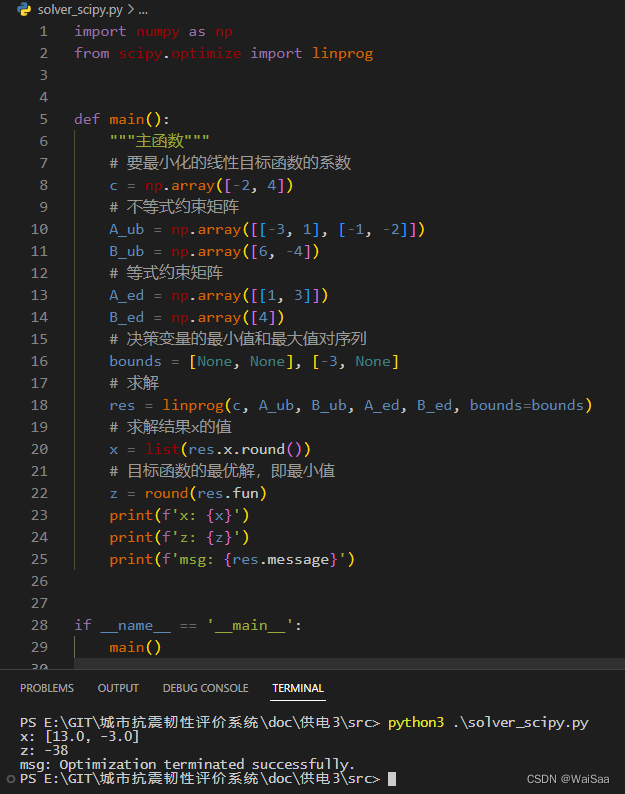
2、多個決策變量-cvxpy
cvxpy幾個決策變量都行哈,單個也行。我這里只是用不同的方式實現記錄下。
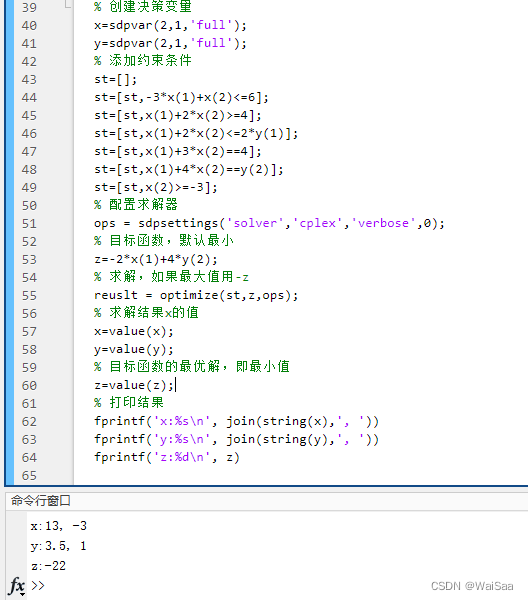
2.1、matlab+yalmip+cplex實現
% 創建決策變量
x=sdpvar(2,1,'full');
y=sdpvar(2,1,'full');
% 添加約束條件
st=[];
st=[st,-3*x(1)+x(2)<=6];
st=[st,x(1)+2*x(2)>=4];
st=[st,x(1)+2*x(2)<=2*y(1)];
st=[st,x(1)+3*x(2)==4];
st=[st,x(1)+4*x(2)==y(2)];
st=[st,x(2)>=-3];
% 配置求解器
ops = sdpsettings('solver','cplex','verbose',0);
% 目標函數,默認最小
z=-2*x(1)+4*y(2);
% 求解,如果最大值用-z
reuslt = optimize(st,z,ops);
% 求解結果x的值
x=value(x);
y=value(y);
% 目標函數的最優解,即最小值
z=value(z);
% 打印結果
fprintf('x:%s\n', join(string(x),', '))
fprintf('y:%s\n', join(string(y),', '))
fprintf('z:%d\n', z)
- 運行結果
x:13, -3
y:3.5, 1
z:-22
2.2、python3+cvxpy+cplex實現
- 需要先安裝
cvxpy和cplex庫
pip3 install cvxpy
pip3 install cplex
- 實現代碼
import cvxpy as cp# 創建決策變量
x = cp.Variable(2)
y = cp.Variable(2)# 添加約束條件
constraints = []
constraints += [-3 * x[0] + x[1] <= 6]
constraints += [x[0] + 2 * x[1] >= 4]
constraints += [x[0] + 2 * x[1] <= 2 * y[0]]
constraints += [x[0] + 3 * x[1] == 4]
constraints += [x[0] + 4 * x[1] == y[1]]
constraints += [x[1] >= -3]# 定義目標函數
objective = -2 * x[0] + 4 * y[1]# 創建模型求解
problem = cp.Problem(cp.Minimize(objective), constraints)
problem.solve(solver=cp.CPLEX, verbose=False)# 打印結果
x = list(x.value)
y = list(y.value)
# 目標函數的最優解,即最小值
z = round(problem.value)
print(f'x: {x}')
print(f'y: {y}')
print(f'z: {z}')- 運行結果
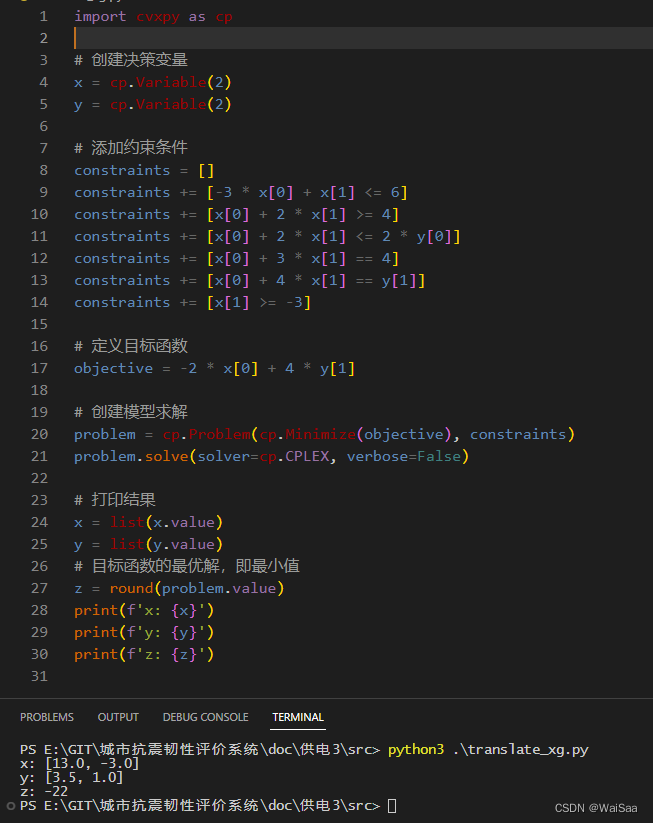
最終可以看到不同的實現方式,運行結果都是一樣的。






)










)

