Prim算法和Kruskal算法都是用于解決最小生成樹問題的經典算法,它們在不同情況下有不同的適用性和特點。
Prim算法:
Prim算法是一種貪心算法,用于構建一個無向圖的最小生成樹。算法從一個初始節點開始,逐步添加與當前樹連接且具有最小權重的邊,直到所有節點都被連接。Prim算法的基本思想是從一個起始節點出發,每次選擇一個與當前最小生成樹相連的節點中,權重最小的邊,將這個節點加入最小生成樹中,并將其相連的邊考慮進來。這樣逐步擴展最小生成樹,直至所有節點都被包含。
Kruskal算法:
Kruskal算法也是一種貪心算法,用于構建一個無向圖的最小生成樹。該算法首先將圖中的所有邊按照權重從小到大進行排序,然后從最小權重邊開始,依次將邊加入生成樹中,但要保證加入邊不會形成環。如果加入某條邊會導致環的形成,則放棄該邊,繼續考慮下一條權重較小的邊,直到生成樹中包含了所有的節點。
區別:
基本思想:Prim算法從一個起始節點開始,逐步添加與當前最小生成樹相連的具有最小權重的邊。Kruskal算法通過排序邊,然后逐個添加邊,保證不形成環。
頂點處理:Prim算法在每一步選擇中,僅考慮與當前已選擇頂點相連的頂點,直接操作頂點。Kruskal算法是通過遍歷邊的方式進行操作,不直接關心頂點。
數據結構:Prim算法通常使用優先隊列(最小堆)來維護待選的邊,以便每次選擇具有最小權重的邊。Kruskal算法則通常使用并查集來判斷是否會形成環。
性能:在邊的數量較少,而頂點的數量較多時,Prim算法通常會更有效。而在邊的數量較多,而頂點的數量較少時,Kruskal算法可能更適用。
復雜度:Prim算法的時間復雜度通常在 O(V^2) 到 O(E* log(V)) 之間,取決于實現方式。Kruskal算法的時間復雜度主要由排序邊的復雜度決定,通常為 O(E * log(E))。
總的來說,兩種算法都能有效地構建最小生成樹,但在不同情況下選擇合適的算法可以提高效率。
1135. 最低成本聯通所有城市
想象一下你是個城市基建規劃者,地圖上有 n 座城市,它們按以 1 到 n 的次序編號。
給你整數 n 和一個數組 conections,其中 connections[i] = [xi, yi, costi] 表示將城市 xi 和城市 yi 連接所要的costi(連接是雙向的)。
返回連接所有城市的最低成本,每對城市之間至少有一條路徑。如果無法連接所有 n 個城市,返回 -1
該 最小成本 應該是所用全部連接成本的總和。

代碼實現:
// 定義邊
struct Edge{int city;int cost;
};// 定義 邊的比較方法
// cost值較小的Edge對象具有更高的優先級,
// 因為EdgeComparator在a的cost大于b的cost時返回true,
// 這意味著在優先級隊列中,a應該在b之后。
// 所以,這個優先級隊列是一個最小堆(min heap),即隊列頂部總是cost最小的Edge對象
struct EdgeComparator{bool operator()(const Edge& a,const Edge& b){return a.cost>b.cost;}
};class Solution {
public:int minimumCost(int n, vector<vector<int>>& connections) {// 連接所有點需要的costint cost = 0;vector<vector<Edge>> edges(n+1);// 定義訪問數組vector<bool> visited(n+1,false);// 定義優先隊列, cost小的排在前面priority_queue<Edge, vector<Edge>, EdgeComparator> minHeap;visited[1] = true;// 從城市1開始// 建立Edge二維數組// 每個點會對應一個list,每個list中存儲:和這個點相連的城市以及到相連城市的距離for(const auto& conn:connections){// 是雙向的edges[conn[0]].push_back(Edge{conn[1],conn[2]});edges[conn[1]].push_back(Edge{conn[0],conn[2]});}// 先把和1點相連的Edge進行排序,放入優先隊列for(const Edge& edge:edges[1]){minHeap.push(edge);}// 連接點的數量,初始為1int count = 1;while(!minHeap.empty()){Edge e = minHeap.top();minHeap.pop();if(visited[e.city]){// 如果已經訪問過某一點了,則直接進入下一次循環continue;}// 如果沒有訪問過,就設置為truevisited[e.city] = true;// 再把和這個點相連的Edge push進優先隊列for(const Edge& edge:edges[e.city]){minHeap.push(edge);}cost += e.cost;// 連接點的數量+1count++;if(count == n){return cost;}}return -1;}
};
1584. 連接所有點的最小費用
給你一個points 數組,表示 2D 平面上的一些點,其中 points[i] = [xi, yi] 。
連接點 [xi, yi] 和點 [xj, yj] 的費用為它們之間的 曼哈頓距離 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的絕對值。
請你返回將所有點連接的最小總費用。只有任意兩點之間 有且僅有 一條簡單路徑時,才認為所有點都已連接。
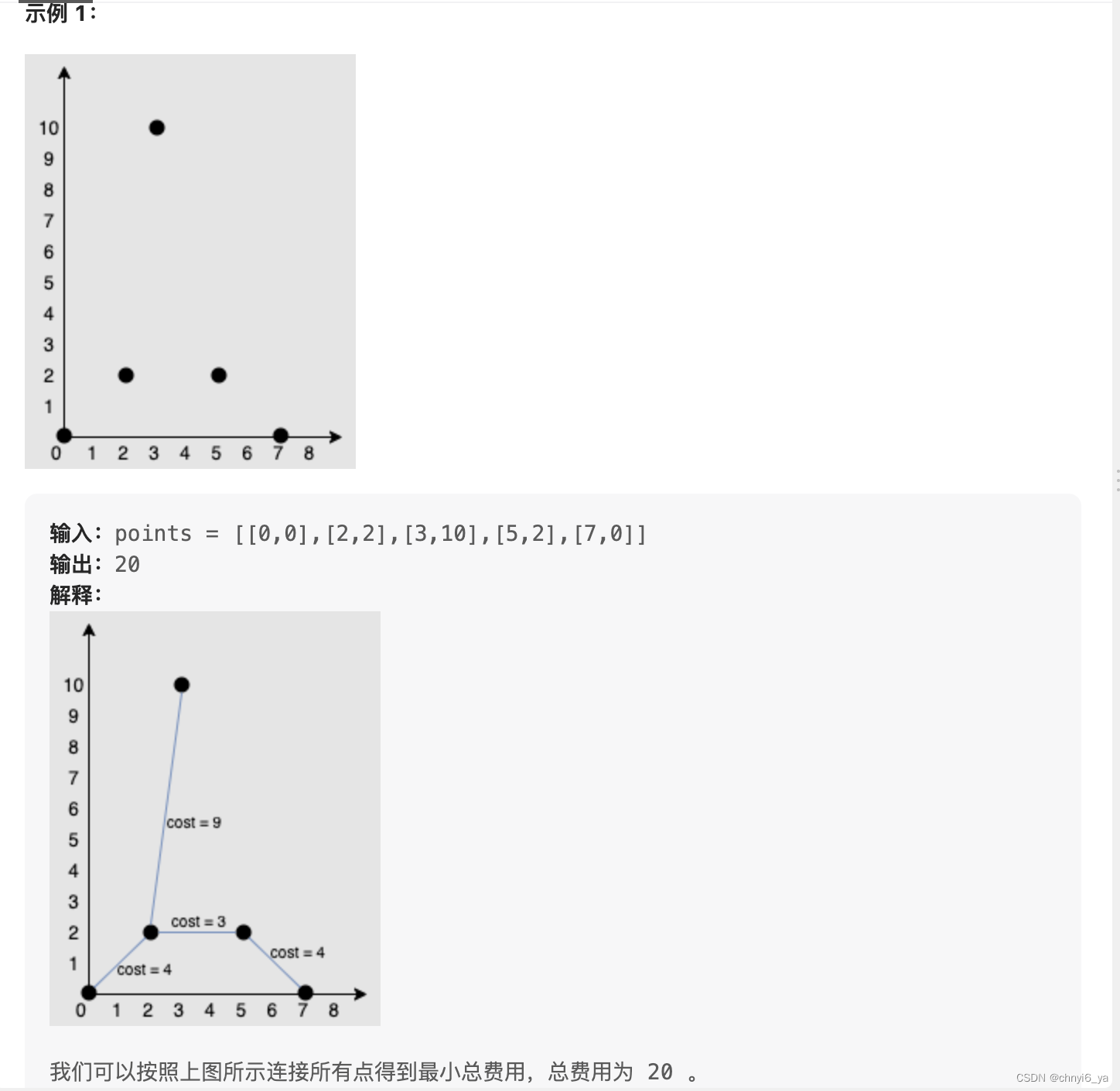
完全仿照上面一題的代碼,寫出了這題的代碼,唯二的區別在于,需要自己額外計算一下每個點之間的距離,并且不滿足條件時返回0:
// 定義結構體Edge
struct Edge{int city;int cost;
};struct EdgeComparator{bool operator()(const Edge& a,const Edge& b){return a.cost>b.cost;}
};// 計算曼哈頓距離
int compute_Manhattan(vector<vector<int>>& points,int p1,int p2){return abs(points[p1][0]-points[p2][0]) + abs(points[p1][1]-points[p2][1]);
}class Solution {
public:int minCostConnectPoints(vector<vector<int>>& points) {int cost = 0;int n = points.size();// 點的個數vector<vector<Edge>> edges(n);priority_queue<Edge, vector<Edge>, EdgeComparator> minHeap;vector<bool> visited(n,false); // 訪問數組visited[0] = true; // 從0點開始searchint count = 1; // 已經訪問到了的點(已經相連的點)// 建立了 鄰接表for(int i = 0;i<n-1;i++){for(int j = i+1;j<n;j++){// 兩點間的曼哈頓距離int distance = compute_Manhattan(points,i,j);edges[i].push_back(Edge{j,distance});edges[j].push_back(Edge{i,distance});}}// 把和0點相關的點push進最小堆for(const Edge& edge:edges[0]){minHeap.push(edge);}while(!minHeap.empty()){Edge e = minHeap.top();minHeap.pop();if(visited[e.city]){// 如果已經訪問過該點,則進入下一次循環continue;}visited[e.city] = true; // 標記訪問過該點// 再把和該點相連的點push 進 minHeapfor(const Edge& edge:edges[e.city]){minHeap.push(edge);}cost += e.cost; // 加上和這個點相連的costcount++;if(count == n){// 如果n個點都相連了,返回cost即可return cost;}}return 0;}
};
)



ADC設備(RTT保姆級介紹))





——Centos7設置時間為網絡時間)
,訓練預測自己的【中文文本多分類】)







