為節省篇幅，不標注文章來源和文章的問題場景。大部分是我的通俗理解。

向量關于向量的偏導數：雅可比矩陣

二階導數矩陣：海森矩陣

多元函數的二階偏導數構成的方陣，對稱。

隨機變量

隨機變量是樣本點的函數。

隨機場

一個例子是，平面上的每一個點都是一個隨機變量。
隨機場強調空間，跟隨機過程一樣，都是一系列隨機變量的集合。

伽馬函數

階乘在實數集上的延拓。比如說，2.5!。推導過程只有兩行，見百度百科。

beta分布

beta分布可以從二項分布推導。
以下圖為例講解吧，

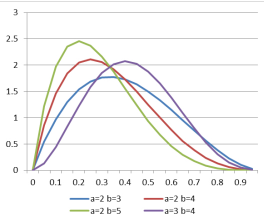
a+b可以理解為實驗次數。如a=2，b=3，拋5次硬幣，a=2表示5次中有兩次朝上。如果硬幣朝上的概率為0.3，那么可能性會較硬幣朝上概率為0.8時大。此處的縱軸不表示概率（因為要保證概率歸一，即曲線下面積為1），但可以體現出概率的相對大小。
至于狄利克雷分布，是beta分布的高維推廣。

數學術語

• 算子是一個函數到另一個函數的映射，它是從向量空間到向量空間的映射
• 泛函是函數（向量空間）到數域的映射
• 函數是從數域到數域的映射

閉式解=解析解，即獲得一個解函數，這個解函數有通用性，即能幫我們計算不同情況下的解。
與閉式解對應的，是數值解，可以認為是給定情況下能解出來一個足夠精度的解，但換一種情況后之前的解就沒用了。

配分函數partition function，所有狀態的和，放在分母上就能起到歸一作用。

坐標上升法

多元函數，求極值。每次固定n-1元，求自由元偏導，令偏導為0，就能得到一個自由元=f(固定元)的更新式。把所有更新式都求出來之后，開始迭代。

協方差

協方差經常也用來衡量兩個隨機變量之間的線性相關性。如果兩個隨機變量的協方差為0，那么稱這兩個隨機變量是線性不相關。
兩個隨機變量之間沒有線性相關性，并非表示它們之間是獨立的，可能存在某種非線性的函數關系。反之，如果X與Y是統計獨立的，那么它們之間的協方差一定為0。
協方差矩陣是在兩個隨機向量上討論的。協方差矩陣中的元素，對應兩個隨機變量的協方差。
核函數，可以衡量兩個樣本之間的相似度。計算協方差矩陣時，有若干種核函數可以選擇。

訓練集，驗證集，測試集，交叉驗證

訓練集，訓練獲得最佳參數。
驗證集（強調調超參作用時，也有叫開發集的），調超參，如在神經網絡中選擇隱藏單元數、廣義線性回歸中的多項式次數、控制權值衰減的λi等。一般由專家經過經驗或者實驗選定。控制模型復雜程度（如果訓練集準確率提升，而驗證集準確率下降，說明過擬合，模型過于復雜，應該停手）。
測試集，測試泛化能力。
交叉驗證，由于數據有限，劃為k份之后，用多種分配方案來劃分為三種集合。

凸函數

一階導單調增，或者用兩點連線在函數圖像上方來判斷。
損失函數必須是凸函數，以免梯度下降時陷入局部最優解。

學習曲線

偏差大，是欠擬合。方差大，是過擬合。
欠擬合，可以增加特征。減小正則項。提高模型復雜度。
過擬合，可以減少特征。擴大數據集。增大正則項。降低模型復雜度。

TF-IDF

用于關鍵字提取。
字詞在文件中出現次數越多，則越重要；
字詞在文件集中出現次數越多，則越不重要。
TF，term frequency，定義為出現次數/文章詞數
IDF，inverse document frequency，定義為log(總文章數/出現文章數)。

分層聚類

自底向上，先定義距離，每次將距離最小的類合并。
定義一個最大最小值，如果相距最近的類的距離大于它，就停止聚類。決定了是將層分得細一點還是粗一點。
可見，效果取決于距離的定義，和最大最小值的設置。

萬能近似定理，神經網絡到底在干什么

譯自universal approximation theorem。
https://blog.csdn.net/guoyunfei20/article/details/78288271
萬能近似定理意味著無論我們試圖學習什么函數，我們知道一個大的MLP（多層感知機）一定能夠表示這個函數。
兩層的前饋神經網絡可以擬合任意有界閉集上的任意連續函數。
這也解釋了神經網絡在“學什么”，就是在學一個函數。
這個函數的作用是，把輸入的低維特征，變成更加抽象的高維特征。
基本的深度學習相當于函數逼近問題，即函數或曲面的擬合，所不同的是，這里用作基函數的是非線性的神經網絡函數，而原來數學中用的則是多項式、三角多項式、B-spline、一般spline以及小波函數等的線性組合。
由于神經網絡的非線性和復雜性（要用許多結構參數和連接權值來描述），它有更強的表達能力，即從給定的神經網絡函數族中可能找到對特定數據集擬合得更好的神經網絡。這相信正是深度學習方法能得到一系列很好結果的重要原因。直觀上很清楚，當你有更多的選擇時，你有可能選出更好的選擇。當然，要從非常非常多的選擇中找到那個更好的選擇并不容易。

state-of-the-art，baseline，benchmark

表示“目前最好的”。比如state-of-the-art model，就是“目前領域內最好的模型”。
偶爾會用SOTA 來簡寫 state-of-the-art。
“舉個例子，NLP任務中BERT是目前的SOTA，你有idea可以超過BERT。那在論文中的實驗部分你的方法需要比較的baseline就是BERT，而需要比較的benchmark就是BERT具體的各項指標。”（知乎 許力文 MorrisXu）

知識

什么是知識，知識是非結構/半結構化數據經過處理后得到的結構化數據，比如下面提到的，關系抽取中的關系三元組，以及事件提取中的事件描述表格。相較文本，提煉出的結構化的表格更容易查詢，體積也更小。

從文本中獲取知識，有兩個重要的步驟，關系提取和事件提取。

關系抽取

https://blog.csdn.net/mch2869253130/article/details/117199565 （提到了一些經典論文）
關系抽取主要做兩件事：

• 識別文本中的subject和object（實體識別任務）
• 判斷這兩個實體屬于哪種關系（關系分類）

全監督關系抽取任務并沒有實體識別這一子任務，因為數據集中已經標出了subject實體和object實體分別是什么，所以全監督的關系抽取任務更像是做分類任務。模型的主體結構都是特征提取器+關系分類器。特征提取器比如CNN，LSTM，GNN，Transformer和BERT等。關系分類器用簡單的線性層+softmax即可。

相對全監督，也有半監督。基礎是距離監督假設：如果知識庫中的實體對之間存在關系，那么每個包含該實體對的文檔都會表達該關系。這個假設太強，因此提出多示例學習和多種降噪方法。

關系提取，是為了獲得（主體，關系，客體）的三元組。關系提取的發展，先是全監督，全監督的問題主要是數據標注不足，于是提出半監督，半監督的主要問題是假設太強、噪聲太大，更前沿的研究聚焦于如何弱化假設和降噪。深度學習可以用于全監督關系提取。

事件提取

指定schema（感興趣的類型，事件觸發詞、要素（如時間地點人物）），然后判斷類型、提取要素，從而將文本變成表格。

事件提取，識別特定類型的事件，并把事件中擔任既定角色的要素找出來。比如說，識別“企業成立”這一事件，需要靠事件觸發詞“成立”“創辦”，需要提取出時間、地點、人物、注冊資金等要素。傳統上需要外部NLP工具（如依存分析、句法分析、詞性標注），有時還需要人工設計特征。使用深度學習進行事件提取則可以減少對外部NLP工具的依賴，并自動提取特征。

誤差累積

一個常見的老大難問題（如果沒啥可說的，可以提一下。不過也確實有針對這個問題的工作。）
所有的pipeline式的方法都會有這個問題。簡單來說，如果前面的步驟錯了，后面的步驟只會是錯上加錯。
相應的，有joint式的方法。中文可分別譯作流水線模型和聯合模型。

零樣本學習

屬于遷移學習。利用類別的高維語義特征（有尾巴、有條紋，標簽空間）代替樣本的低維特征（圖像特征，特征空間），使得訓練出來的模型具有遷移性。
低維升高維很類似接近人類的思考過程，感覺是人類比能力的基礎。
傳統上，模型需要某類型足夠多的數據，才能足夠了解一個類，才能判斷新物體是否屬于這個類。
最初，令輸入都是未知類（即測試集與訓練集沒有交集）。但實用價值有限。后來發展，輸入中可以有已知類也可以有未知類。

集成學習

思路是博采眾長。
按學習器的種類，可以分為同質和異質。
按學習器間的依賴關系，可以分為串行和并行。

同質常用的模型是cart決策樹和神經網絡。
串行的代表是boosting，使前面學習器誤差率高的樣本，會獲得更大的權重。
并行的代表是bagging。隨機森林使bagging的特殊情況，其學習器都是決策樹。

除了學習器的種類和依賴，還需要考慮如何結合。可以用平均法、投票法、學習法。
學習法是指，用多個初學習器的輸出，作為次學習器的輸入。

敏感詞審核

一般使用DFA算法。

用于文本審查的神經網絡算法

考慮到對上下文關聯的分析，神經網絡采取LSTM long short-term memory。
LSTM是RNN recurrent neural network的特殊類型，利用RNN上下層的動態相關性，學習長期依賴信息，
因此LSTM對文本中的上下文關系有較好的理解。

TextCNN是利用CNN來處理文本分類任務，它利用CNN捕捉局部相關性的特點，來提取句子中的關鍵信息，從而進一步進行文本樣本的特征提取，實現更準確的分類。CNN+LSTM的模型是結合CNN和LSTM網絡，先使用CNN做局部特征提取，再用LSTM提取上下文關聯信息。

準確率，精確率，召回率，F-measure

機器學習性能評估的參數（來自知乎答主Charles Xiao）
假設我們手上有60個正樣本，40個負樣本，我們要找出所有的正樣本，系統查找出50個，其中只有40個是真正的正樣本，計算上述各指標。
TP: 將正類預測為正類數 40
FN: 將正類預測為負類數 20
FP: 將負類預測為正類數 10
TN: 將負類預測為負類數 30
準確率(accuracy) = 預測對的/所有 = (TP+TN)/(TP+FN+FP+TN) = 70%
精確率(precision) = TP/(TP+FP) = 80%，
召回率(recall) = TP/(TP+FN) = 2/3，

F-measure是精確率和召回率的調和平均。

應用場景，
準確率不適合樣本不均衡的情況，假如有90%的正樣本，那么常數函數也能有90%的準確率。
精確率也叫查準率。當你說它為正的時候，我有多大把握相信你。
召回率適合只關心一類樣本的情況，比如網貸違約，寧可誤報也不能漏報。召回率也叫查全率。你找出了多少正類。
PR曲線指的是precision和recall，很難兩全。
至于ROC，可以解決樣本不均衡的情況，它考慮的是正查準率和1-負查準率。

Inter-rater agreement Kappas

inter-rater agreement，評分者之間的共識。
可以從側面反映人工標注的質量。Kappas越高，說明評分者越一致。

RNN和LSTM

下面這個鏈接，是我目前看到的講得最清楚的。
https://zhuanlan.zhihu.com/p/40119926

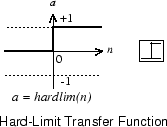
hard-limit

NLP的預訓練

在互聯網上有一些基于海量語料(例如中文維基百科等)的預訓練詞向量。但是一方面由于詞庫過于龐大，勢必要用更多維數去表示，詞向量就會更加冗長和稀疏；另一方面，某些詞在特定場景具有特指的含義。因此，有時通用的預訓練詞向量不適合直接拿來使用，而應基于場景問題域本身的語料重新進行詞向量訓練。

詞嵌入中的K

詞向量的維數K是一個超參數。K的取值與語料內包含的不同詞匯個數相關，可依據經驗或由封裝函數進行優化設置。

NLP輸入數據處理

輸入的維數要相同，而句子包含的詞數不同。一種方法是截斷和補齊。

神經網絡實現

keras的封裝程度比tensorflow更高，tensorflow比pytorch的封裝程度更高。

特征提取

相比之前提到的關系提取和事件提取，特征提取的應用更加廣泛。分類、聚類都可能用到。
一是對原始數據進行某種變換；二是在變換的過程中使不同的類別（或不同樣本）具有相對較好的區分性。
效果上，對原始數據進行了提煉和加工。一般來說，特征提取的特征維數會低于原始特征，體積會大大縮小。
主成分分析（Principal components analysis，PCA）與線性鑒別分析（Linear Discriminant Analysis，LDA）最為經典。

LDA

Linear Discriminant Analysis和Quadratic Discriminant Analysis并列。
LDA會將k維數據投影到k-1維的超平面，因此也具有demension reduction的作用。不同于PCA會選擇數據變化最大的方向，LDA會主要以類別為思考因素，使得投影后的樣本盡可能可分。
使得相同類別在該超平面上的投影之間的距離盡可能近，同時不同類別的投影之間的距離盡可能遠，在LDA中，我們假設每一個類別的數據服從高斯分布，且具有相同協方差矩陣。
Quadratic Discriminant Analysis類似于LDA，不同的地方是它可以形成非線性的邊界，并且不同的類所屬的高斯分布具有不同的協方差矩陣。
思想和triplet loss有點像，都是最小化類內間距 ，最大化類間間距。

PCA

經典的降維方法。
會產生一些新特性，新特性可以是舊特性的線性組合。從而可以用更少的維數、很少的信息損失來描述物件。
方差，其實就是辨識度的代名詞。我們尋找最有辨識度的特征，就是尋找一種測度，使樣本之間的方差最大。
誤差，其實就是信息損失的代名詞。我們希望降維過后仍能“重建”原始數據。
看下圖，想象原點固定、旋轉的平面坐標系。什么時候樣本的方差最大？

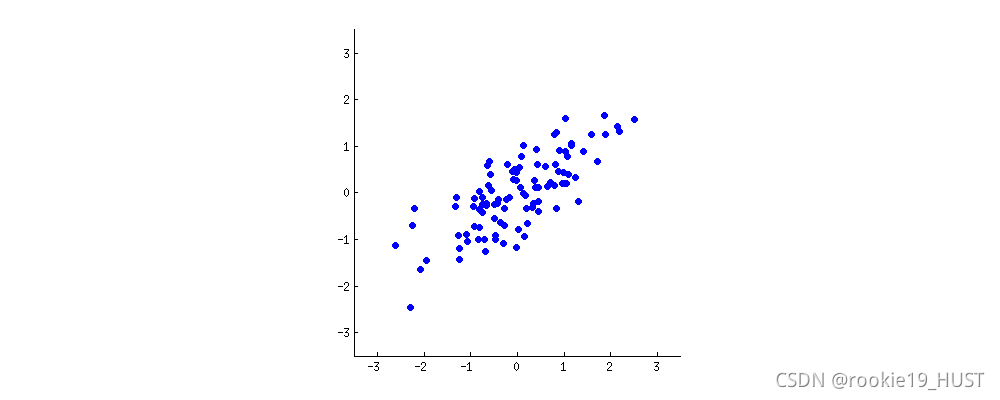
旋轉的過程，就是將舊的兩個指標進行不同比例線性組合的過程。基就是指標，就是測度。
達到最大方差的同時，也達到了最小誤差。
方差是投影點到投影線中心的距離（的平方），誤差是原點到投影點的距離（的平方），其和始終為原點到投影線中心的距離（勾股定理）。所以最大方差，最小誤差會同時達到。
至于為什么要投影，投影其實就是降維了。

從上面的例子也可以看出，PCA可以合并原始特征中線性相關的特征。至于非線性相關，可以了解一下kernel PCA。
關于PCA更嚴謹的原理，需要了解協方差矩陣和奇異值分解。

CRF 條件隨機場

隨機場，場中有若干位置，按分布給位置賦值，則為隨機場。
馬爾科夫隨機場，每一個位置的賦值只與相鄰位置有關。
條件隨機場，輸入為單變量X，輸出為單變量Y的馬爾科夫隨機場。
如果條件隨機場的輸入x和輸出y有相同的結構，則為線性鏈條件隨機場。

總結一下就是，tk是局部特征函數（節點與相鄰節點，可見馬爾可夫性），sk是節點特征函數（節點），兩者前面的系數代表可信度，Z是規范化。

一個應用是詞性標注。因為詞性標注適合用條件隨機場建模（也具有馬爾可夫性）。

DL和NLP當年為什么不火

其實技術成熟度只是一個方面。另一個重要原因是沒有數據。
數據量級的發展速度，我認為是快于所謂“技術”的發展速度的。
早年，NLP的數據很多都來自報紙這樣的傳統媒體。

詞袋bow

把句子看成單詞的集合，統計詞出現的次數。
將非結構化的語言轉化為結構化的map。
統計所有詞會導致維度過高，也就是map中key太多，而且會很稀疏（平均value很小）。去掉停止詞是方法之一。
詞袋模型的應用之一是，結合距離定義，來對比文本相似度。
詞袋模型的問題是，無法反映詞之間的關聯（比如主賓互換后仍然相似），而且無法捕捉否定關系（肯定句和否定句仍然相似）。
同樣是詞頻，TF-IDF則多考慮了逆文檔頻率，與BoW不同。

n-gram

基于統計，判斷連詞成句的概率。
n是滑動窗口size，一般取2或者3，太大時有V的n次方種可能。詞袋是n=1。
一個句子出現的概率，等于一連串條件概率的乘積。馬爾可夫性可以簡化計算。
n-gram的應用之一是智能聯想。
當然，n-gram和詞袋一樣，n-gram統計結果也能作為文本特征，用于分類任務。
有character n-gram和token n-gram之分。

依存分析

處于支配地位的成分稱之為支配者（governor，regent，head），而處于被支配地位的成分稱之為從屬者（modifier，subordinate，dependency）。
以謂語為中心（如下圖的cancel），研究句子中詞與詞的關系。

（圖來自CSDN flying_1314）

type dependency

也是分析句子中詞與詞的關系，出現頻率很高。與依存分析的關系尚不清楚。
記得看stanford manual。

情感分析

這其實是NLP的一個簡化子問題，把“理解”這個高級而難以實現的目標，變成了三分類問題（負面、中性、正面）。
情感分析的目標是，找出文檔中的觀點，甚至觀點的限定條件和原因。
觀點，就是（評價對象，對象屬性，情感強度，評價者身份，時間）。
情感強度可以量化，比如-2~+2。表示負面/正面情感。
主要應用就是商品和服務的評論分析。西方還可用于選舉分析等。
諷刺句是情感分析的難點。

社交媒體文本分析

長度短，不正式，網絡用語，表情
針對社交媒體的不規范性，一般需要文本標準化和nlp工具再訓練。
文本標準化的意思，比如heyyyyyy要規范成hey。
nlp工具再訓練的意思，分詞器POS/依存語法分析器/命名實體識別器NER等工具都是由報紙等傳統數據訓練出來的，需要在此基礎上用社交媒體文本進行再訓練。

wordnet

英文近義詞詞典。來自普林斯頓。

相對熵(KL散度)，交叉熵，JS散度，Wasserstein推土機距離

https://zhuanlan.zhihu.com/p/25071913
https://zhuanlan.zhihu.com/p/74075915
叫熵已經不太直觀了，直觀上應該叫距離（不過不滿足距離的對稱性和三角不等式）。作用是衡量兩個概率分布的距離，衡量預測值和實際值的差異。


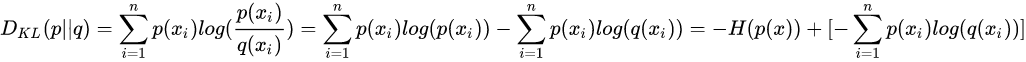
可以看見交叉熵和KL散度之間相差一個常數（實際值的熵）。

JS散度是KL散度的變體，解決對稱性的問題。

推土機距離的式子我都看不懂。直覺上上面兩篇文章都很好。

Wasserstein距離相比KL散度、JS散度的優越性在于，即便兩個分布沒有重疊，Wasserstein距離仍然能夠反映它們的遠近。
可以看出，兩個分布沒有重疊時，KL會是0，這就是梯度消失。
推土機距離就是為了解決這個問題。WGAN在2017年提出。

浪潮起因

第一，硬件發展，如GPU。
第二，數據量來了。
第三，深度學習能從歐氏空間數據中提取潛在特征。

正則化項

翻譯成正則不好，看不出“額外的約束”的意思。
目的是懲罰，比如懲罰復雜模型，懲罰譯文長度。
比如說L1范數，是參數系數絕對值的和。所以參數較少的正則項就會較小。從幾何角度（單位矩形）看，容易出0項，也就是能讓參數稀疏。
L2范數則沒有稀疏的作用（從幾何角度看），但它能避免大參數（1²+3²>2²+2²），讓參數普遍較小。如果有部分參數過大，抗擾動能力就不好。
正則化項一般有系數λ。

歐拉公式

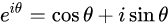
正弦波

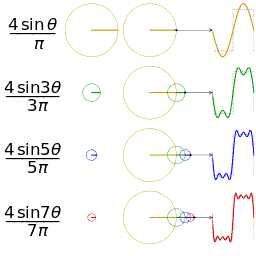
傅里葉級數

周期函數可以表示為正弦波的疊加。
周期性，使有限能代表無限。
頻域分析的結果就是，告訴你具體用哪些正弦波能疊出來。

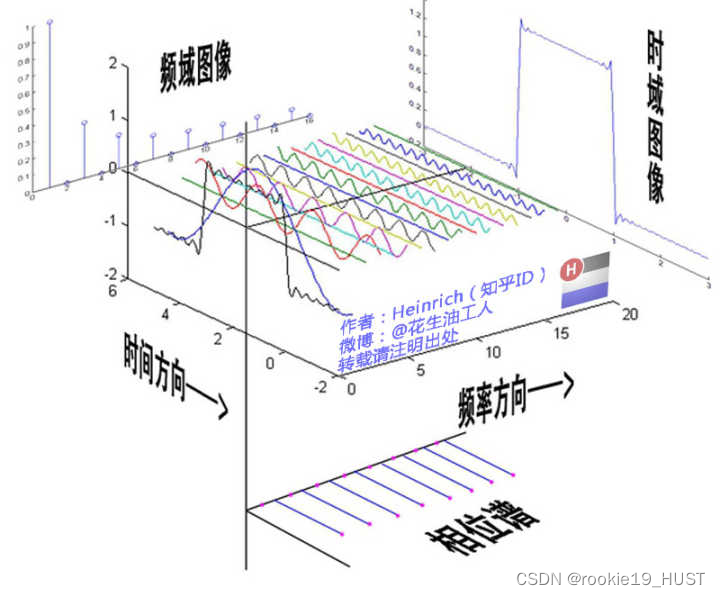
傅氏變換將信號投影到正交空間，看上圖就能理解了。
從側面看只有振幅信息，從下面看可以做出相位譜。
傅里葉級數，時域中周期、連續，頻域中非周期、離散。

傅里葉變換

將一個時域非周期的連續信號（周期無窮大），轉換為一個在頻域非周期的連續信號。
對于有限區間非周期函數，可以通過復制的方法變成周期函數。
將函數投影到正交空間，在正交空間解決問題，再逆變換。典型例子是卷積定理，嫌卷積麻煩，那就先做傅氏變換，在正交空間做乘法，然后再反變換。

傅里葉變換的應用

濾波，去除特定的頻率。在頻域很容易做到，減少一根棍子就行。
解微分方程、計算卷積。復變函數課程中大家都學過。原理是微分積分變成了乘除法。想不起來了的話，可以翻一翻“常用傅里葉變換表”找找感覺。

卷積

兩個函數參與卷積，輸出另一個函數。
一個輸入是輸入信號，另一個輸入代表系統。
翻轉，乘積，滑動。在使用特定的卷積核時，可以看成滑動平均。
一個域中的卷積相當于另一個域中的乘積。
任意信號f(t)可表示為沖激序列之和，跟沖激函數的卷積。

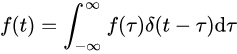
積分，就是先分割再累加。看看上式，可以理解，跟沖激函數卷積，相當于先分割為無數脈沖，再累加。
t決定兩個函數的相對位置。在不同的相對位置下，求重疊面積，就得到輸出函數在此位置的值。
據wiki，整數乘法和多項式乘法都是卷積。
圖像處理中，用作圖像模糊、銳化、邊緣檢測。
統計學中，加權的滑動平均是一種卷積。
概率論中，兩個統計獨立變量X與Y的和的概率密度函數是X與Y的概率密度函數的卷積。

fine tuning

指微調。

RELU/sigmoid/tanh

據wiki，增強網絡的非線性特性。ReLU函數更受青睞，這是因為它可以將神經網絡的訓練速度提升數倍，而并不會對模型的泛化準確度造成顯著影響。

池化層，池化

非線性形式的降采樣。“最大池化（Max pooling）”是最為常見的。它是將輸入的圖像劃分為若干個矩形區域，對每個子區域輸出最大值。

卷積層，邊緣探測

卷積層可以發現邊緣。
邊緣探測的基本過程，先灰度化，再用低通濾波器降噪，用高通濾波器提取邊緣，最后二值化。如圖。

在CNN用于圖像處理時，卷積核=濾波器=矩陣，圖像卷積如圖:

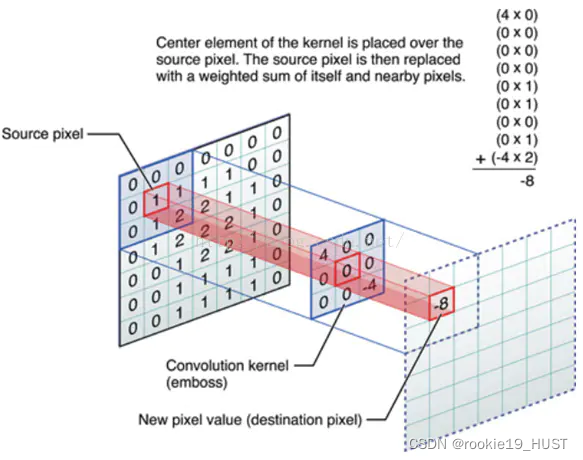
從結果來看，輸出的是原圖的邊緣。這其實也是一種特征提取。網絡的每一層輸出都可以視為特征。
學習的過程，其實是尋找合適的卷積核的過程（對于邊緣檢測，已經有一些廣泛使用的卷積核）。卷積核就是參數矩陣。

channel 通道

灰度圖像，只有一個通道。RGB是三通道。

歐氏空間、grid、結構化數據

說的都是一件事情。

特征分解和譜分解

幾乎一樣。但譜分解形式上是和式，能讓人聯想到傅里葉級數。

圖的拉普拉斯矩陣為什么叫拉普拉斯矩陣

https://zhuanlan.zhihu.com/p/362416124
關鍵是其中拉普拉斯算子的推廣。

高斯分布：最大熵？

最混亂的應該是均勻分布。不過在限制方差的時候，高斯分布是最大熵模型。
印象中信息論好像學過同義的定理。
有人說，高斯分布是“無知”的。對此我的理解是，它是“穩妥”、“不武斷”的，如果你只知道均值和方差，別人來問你數據是什么分布，你如何回答？你回答相應參數的高斯分布，會比較穩妥。因為這一回答沒有做其它的假設，沒有臆斷，沒有憑空制造什么先驗信息。最大熵意味著這是你能給出的，最寬泛、最不確定的答案，因而說它“無知”、“穩妥”。

triplet loss

triplet三元組，包括a anchor，p positive，n negative。思想是讓a和p的距離小，a和n的距離大。