問題引入

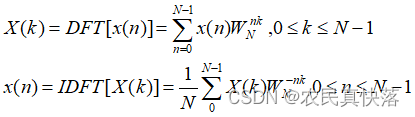
上面是DFT和IDFT的公式，IDFT先不談。在實踐中常使用FFT算法來快速算出DFT，獲得時域采樣信號x(n)的頻率幅度譜。
例如：

N=1500;
xn=0.5*sin(2*pi*75/N*n)+3*cos(2*pi*40/N*n)+0.7*sin(2*pi*350/N*n);

上面這個時域采樣信號xn由三個頻率疊加而成，我們知道頻率的概念是1秒信號經過了多少個周期，
那么我們假設采樣率是fs=1000，共采樣N=1500點，那么0.5*sin(2*pi*75/N*n)的頻率即為75*fs/N=50，因此第一個信號頻率為50。

通過Matlab進行FFT，可以畫出這樣一張頻率幅度譜：

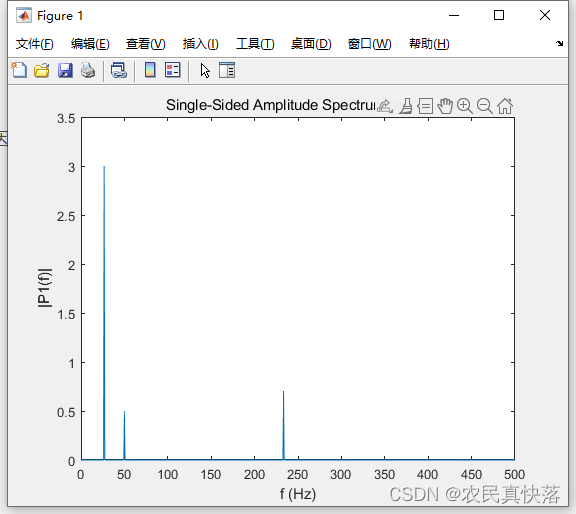
這里就引申出我們的標題：DFT為什么能求頻率幅度譜？DFT后的X[k]與x(n)幅度的關系？DFT/IDFT底層數學原理？
對于這個問題，我看了不少網上的博客、視頻、書籍，總覺得講的不清不楚，有人說X[k]的結果就是x(n)的幅度，有人說X[k]的結果除以N就是x(n)的幅度，有人說X[k]的結果除以N/2就是x(n)的幅度，就沒有一個比較清楚的證明到底X[k]的值和x(n)幅度的關系。
如果你也對此有疑問，現在我證明給你看！

鋪墊一些小公式

要看懂我的證明，首先需要鋪墊一些小公式，防止你不知道！

DFT公式證明

我將公式的證明整理成了PPT，下面我直接復制，在證明中使用到了上面鋪墊的小公式，注意關聯起來看就可以理解了！

DFT公式分解為4部分

先考慮k1=0的情況:

再考慮k1≠0的情況:

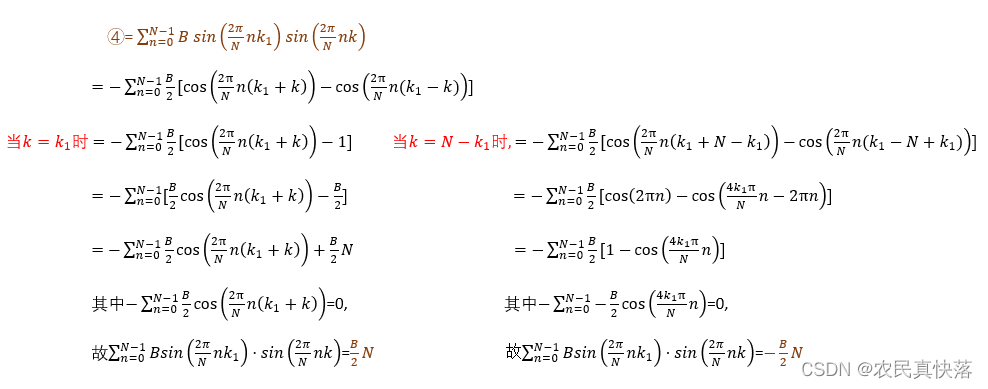
DFT計算后，X(k)與x(n)的關系：

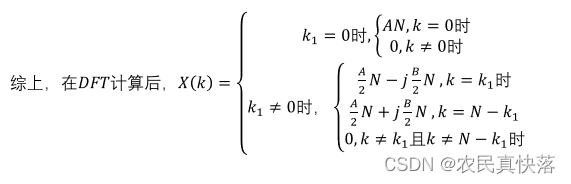
可以看到，DFT公式本質上可以完全拆成三角函數的計算，在此過程中利用
高中的積化和差公式和三角函數在若干個周期的累加為0，
可以得到X[k]和原信號x(n)幅度的關系。

Matlab FFT示例代碼

下面我們給出使用FFT對x(n)進行DFT計算后，繪制頻率幅度譜的Matlab代碼，看官可以發現，這上述公式的X(k)結果是完全對應的！

%功能說明：
%生成時域采樣信號0.5sin(2pi*k/N*n)
%通過fft轉化到頻域，繪制頻率幅度譜，橫坐標是頻率f=k*fs/N，縱坐標是實際幅度
%再通過ifft轉化回時域，繪制ifft結果信號，和原信號進行對比%采樣率1000
fs=1000;%在N個采樣點中，一共振動了k個周期
k=75;%采樣總點數
N=1500;%n表示采樣的第n個點
n=0:N-1;%xn是采樣得到的x(n)時域信號
xn=0.5*sin(2*pi*k/N*n)+3*cos(2*pi*40/N*n)+0.7*sin(2*pi*350/N*n);xk=fft(xn);%abs是求模
P2=abs(xk/N);
P1=P2(1:N/2+1);
P1(2:end-1)=2*P1(2:end-1);%半頻譜 f=k*fs/N
f=fs*(0:(N/2))/N;
plot(f,P1) 
title("Single-Sided Amplitude Spectrum of X(t)")
xlabel("f (Hz)")
ylabel("|P1(f)|")

IDFT公式證明

Matlab調用FFT/IFFT并繪圖

%功能說明：
%生成時域采樣信號0.5sin(2pi*k/N*n)
%通過fft轉化到頻域，繪制頻率幅度譜，橫坐標是頻率f=k*fs/N，縱坐標是實際幅度
%再通過ifft轉化回時域，繪制ifft結果信號，和原信號進行對比%采樣率1000
fs=1000;%在N個采樣點中，一共振動了k個周期
k=75;%采樣總點數
N=1500;%n表示采樣的第n個點
n=0:N-1;%xn是采樣得到的x(n)時域信號
xn=0.5*sin(2*pi*k/N*n)+3*cos(2*pi*40/N*n)+0.7*sin(2*pi*350/N*n);xk=fft(xn);%abs是求模
P2=abs(xk/N);
P1=P2(1:N/2+1);
P1(2:end-1)=2*P1(2:end-1);%半頻譜 f=k*fs/N
f=fs*(0:(N/2))/N;
plot(f,P1) 
title("Single-Sided Amplitude Spectrum of X(t)")
xlabel("f (Hz)")
ylabel("|P1(f)|")% 反傅里葉變換
X = ifft(xk, 'symmetric');% 繪制輸入信號和還原信號的圖像
figure
subplot(2,1,1)
plot(n, xn)
title('Input Signal')
xlabel('Time (s)')
ylabel('Amplitude')subplot(2,1,2)
plot(n, X)
title('Signal after IFFT')
xlabel('Time (s)')
ylabel('Amplitude')