前文從線性回歸和 Logistic 回歸引出廣義線性回歸的概念,很多人還是很困惑,不知道為什么突然來個廣義線性回歸,有什么用?只要知道連續值預測就用線性回歸、離散值預測就用 Logistic 回歸不就行了?還有一些概念之間的關系也沒理清,例如線性回歸和高斯分布、Logistic 回歸和伯努利分布、連接函數和響應函數。
這種困惑是可以理解的,前文為了引導快速入門,從實戰解題的角度推出了答案,但對其背后的概率假設解釋不足,雖然線性回歸專門開辟一節來介紹高斯分布假設,但很多人誤以為這一節的目的只是為了證明最小均方誤差的合理性,Logistic 回歸的伯努利分布假設也需做解釋。
線性回歸是建立在高斯分布的假設上,Logistic 回歸是建立在伯努利分布的假設上。如果不能從概率的角度理解線性回歸和 Logistic 回歸,就不能升一級去理解廣義線性回歸,而廣義線性模型就是要將其它的分布也包納進來,提取這些分布模型的共同點,成為一個模型,這樣再遇到其它分布,如多項式分布、泊松分布、伽馬分布、指數分布、貝塔分布和 Dirichlet 分布等,就可以按部就班地套模型進行計算了。
有些同學不明白的是,「當給定參數 θ?和 x 時,目標值 y 也服從正態分布」,這里 y 服從的是均值為 θTx?的正態分布,當我們訓練得到參數 θ 后,那么對于不同的 x 值,y 服從的就是不同均值的正態分布。伯努利分布也一樣。
要想掌握廣義線性模型,得親自動手做一個實例。
下面我們從概率的角度重新審視線性回歸、Logistic 回歸,來加深對廣義線性模型的理解。
先說線性回歸,假設是 y(i)|x(i);θ~N(θTx(i),σ2),因為 σ2?對 θ?值和 hθ(x) 值沒有影響,所以我們不妨設 σ2=1,那么

把該高斯分布寫成指數分布簇的形式:

?
可得:

根據廣義線性模型的假設,得:

其中 hθ(x)=η 就是響應函數,其反函數就是連接函數。
如果我們有 m 個例子的訓練集 {(x(i),y(i));i=1,...,m},想要學習這個模型的參數 θ,log 似然函數為:
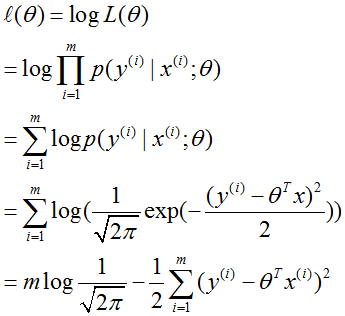
然后最大化該函數即可得解。
再來看 Logistic 回歸,假設是給定 x 和 θ?后的 y 服從伯努利分布。
p(y;Φ)=Φy(1-Φ)1-y
把該伯努利分布寫成指數分布簇的形式:
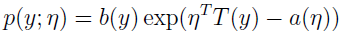

可得:
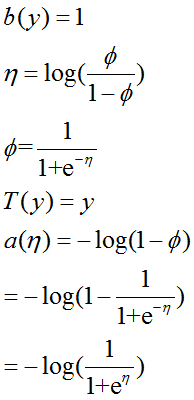
根據廣義線性模型的假設,得:

其中 hθ(x)=1/(1+e-η) 就是響應函數,其反函數就是連接函數。
如果我們有 m 個例子的訓練集 {(x(i),y(i));i=1,...,m},想要學習這個模型的參數 θ,log 似然函數為:
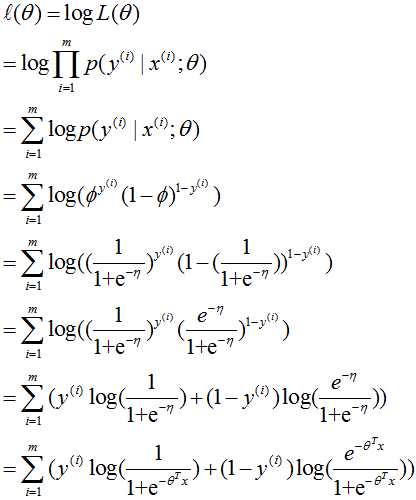
然后同樣最大化該函數即可得解。
?
由此,大致可得使用廣義線性模型的步驟:
1、分析數據集,確定概率分布類型;
2、把概率寫成指數分布簇的形式,并找到對應的 T(y)、η、E(y;x) 等。
3、寫出 log 最大似然函數,不同的分布所使用的連接函數不一樣,并找到使該似然函數最大化的參數值。
?
參考資料:
1、http://cs229.stanford.edu/notes/cs229-notes1.pdf







)











