Video Link

影片連結

We have taken a look at Simple Linear Regression in Episode 4.1 where we had one variable x to predict y, but what if now we have multiple variables, not just x, but x1,x2, x3 … to predict y — how would we approach this problem? I hope to explain in this article.

我們看了第4.1集中的簡單線性回歸，其中我們有一個變量x來預測y ，但是如果現在我們有多個變量，不僅是x，而且還有x1，x2，x3 …來預測y ，我們將如何處理？這個問題？ 我希望在本文中進行解釋。

簡單線性回歸回顧 (Simple Linear Regression Recap)

From Episode 4.1 we had our data of temperature and humidity:

從第4.1集開始，我們獲得了溫度和濕度數據：

We plotted our Data, found and found a linear relationship — making linear regression suitable:

我們繪制了數據，發現并找到了線性關系，從而使線性回歸適用：

We then calculated our regression line:

然后，我們計算了回歸線：

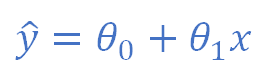
using gradient descent to find our parameters θ? and θ?.

使用梯度下降找到我們的參數 θ?和θ?。

We then used the regression line calculated to make predictions for Humidity given any Temperature value.

然后，我們使用計算得出的回歸線對給定任何溫度值的濕度進行預測。

什么是多元線性回歸？ (What is Multiple Linear Regression?)

Multiple linear regression takes the exact same concept as simple linear regression but applies it to multiple variables. So instead of just looking at temperature to predict humidity, we can look at other factors such as wind speed or pressure.

多元線性回歸采用與簡單線性回歸完全相同的概念，但將其應用于多個變量。 因此，我們不僅可以查看溫度來預測濕度，還可以查看其他因素，例如風速或壓力 。

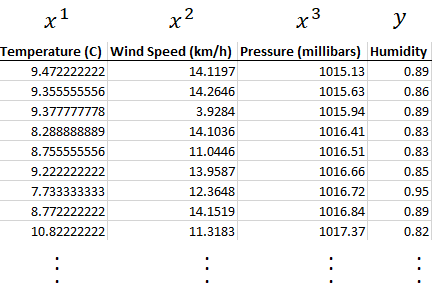
We are still trying to predict Humidity so this remains as y.

我們仍在嘗試預測濕度，因此仍為y。

We rename Temperature, Wind Speed and Pressure to 𝑥1,𝑥2 and 𝑥3.

我們將溫度，風速和壓力重命名為𝑥1 ， 𝑥2和𝑥3。

Just as with Simple Linear Regression we must ensure that our variables 𝑥?,𝑥? and 𝑥? form a linear relationship with y, if not we will be producing a very inaccurate model.

就像簡單線性回歸一樣，我們必須確保變量𝑥?，𝑥_2和𝑥? 與y形成線性關系 ，否則，我們將生成一個非常不準確的模型。

Lets plot each of our variables against Humidity:

讓我們針對濕度繪制每個變量：

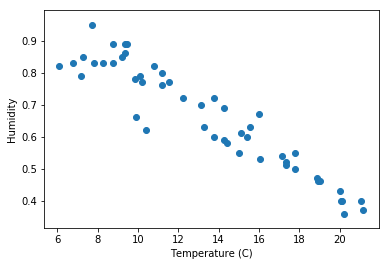
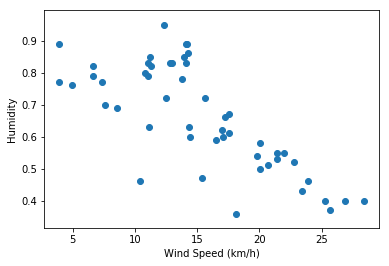
• Temperature and Humidity form a strong linear relationship

  溫度和濕度形成很強的線性關系

• Wind Speed and Humidity form a linear relationship

  風速和濕度形成線性關系

• Pressure and Humidity do not form a linear relationship

  壓力和濕度不是線性關系

We therefore can not use Pressure (𝑥3) in our multiple linear regression model.

因此，我們不能在多元線性回歸模型中使用壓力 (𝑥3)。

繪制數據 (Plotting our Data)

Let’s now plot both Temperature (𝑥1) and Wind Speed (𝑥2) against Humidity.

現在讓我們繪制兩個溫度(𝑥1) 以及相對于濕度的風速(𝑥2)。

We can see that our data follows a roughly linear relationship, that is we can fit a plane on our data that captures the relationship between Temperature, Wind-speed(𝑥?, 𝑥?) and Humidity (y).

我們可以看到我們的數據遵循大致線性關系，也就是說，我們可以在數據上擬合一個平面 ，以捕獲溫度，風速(𝑥?，𝑥2)和濕度(y)之間的關系。

計算回歸模型 (Calculating the Regression Model)

Because we are dealing with more than one 𝑥 variable our linear regression model takes the form:

因為我們要處理多個𝑥變量，所以線性回歸模型采用以下形式：

Just as with simple linear regression in order to find our parameters θ?, θ? and θ? we need to minimise our cost function:

與簡單的線性回歸一樣，為了找到我們的參數θ?，θ?和θ2，我們需要最小化成本函數：

We do this using the gradient descent algorithm:

我們使用梯度下降算法執行此操作：

This algorithm is explained in more detail here

此算法在這里更詳細地說明

After running our gradient descent algorithm we find our optimal parameters to be θ? = 1.14 , θ? = -0.031 and θ? =-0.004

運行梯度下降算法后，我們發現最優參數為θ?= 1.14，θ?= -0.031和θ2= -0.004

Giving our final regression model:

給出我們的最終回歸模型：

We can then use this regression model to make predictions for Humidity (?) given any Temperature (𝑥1) or Wind speed value(𝑥2).

然后，我們可以使用該回歸模型對給定溫度(𝑥1)或風速值(𝑥2)的濕度(?)進行預測。

In general models that contain more variables tend to be more accurate since we are incorporating more factors that have an effect on Humidity.

通常，包含更多變量的模型往往更準確，因為我們納入了更多會影響濕度的因素。

_________________________________________

_________________________________________

潛在問題 (Potential Problems)

When including more and more variables in our model we run into a few problems:

當在模型中包含越來越多的變量時 ，我們會遇到一些問題：

• For example certain variables may become redundant. E.g look at our regression line above, θ? =0.004, multiplying our wind speed (𝑥2) by 0.004 barely changes our predicted value for humidity ?, which makes wind speed less useful to use in our model.
  例如，某些變量可能變得多余。 例如，看一下上面的回歸線θ2 = 0.004，將我們的風速()2)乘以0.004幾乎不會改變我們對濕度predicted的預測值，這使得風速在模型中的用處不大。
• Another example is the scale of our data, i.e we can expect temperature to have a range of say -10 to 100, but pressure may have a range of 1000 to 1100. Using different scales of data can heavily affect the accuracy of our model.
  另一個例子是我們的數據規模，即我們可以預期溫度范圍在-10到100之間，但是壓力可能在1000到1100之間。使用不同的數據規模會嚴重影響我們模型的準確性。

How we solve these issues will be covered in future episodes.

我們如何解決這些問題將在以后的章節中介紹。

上一集 - 下一集 (Prev Episode — Next Episode)

如有任何疑問，請留在下面！ (If you have any questions please leave them below!)