Hello Everyone!

大家好！

I am super excited to be writing another article after a long time since my previous article was published.

自從上一篇文章發表很長時間以來，我很高興能寫另一篇文章。

A Simple Linear Regression [SLR] is basically this formula:

簡單線性回歸[SLR]基本上是以下公式：

which is spelled as y equals b zero plus b one times x one. I am sure you have seen this formula in your high school which was a part of drawing a line or sloped line in a x-y axis. Let’s move a step ahead and understand what each of these variables or coefficients mean in detail.

拼寫為y等于b零加b乘以x一。 我確定您在高中時就已經看到了這個公式，這是在xy軸上繪制直線或傾斜線的一部分。 讓我們前進一步，詳細了解這些變量或系數的含義。

What does y signify in the equation?

y在方程式中代表什么？

根據上式， y是因變量(DV)，它是試圖解釋某些內容的變量，例如： (From the above equation, y is the dependent variable (DV), It is a variable which is trying to explain something, For Example:)

Hypothetically speaking Salary of an employee depends on the years of experience. In this case y that is the salary of an employee would be the dependent variable, since it is dependent on the years of experience.

假設地說，雇員的工資取決于經驗的年限。 在這種情況下，作為雇員薪水的y將是因變量，因為它取決于經驗的年限。

or let’s take another example where the marks scored by the student depends upon the number of hours spent for studying, again in this case y that is the marks scored would be the dependent variable, since it is dependent on the number of hours spent studying for the exam.

還是讓我們再舉一個例子，其中由學生取得的標志取決于花費在這種情況下?學習，再次小時數是進球將因變量的標記，因為它是依賴于所花時間為留學人數考試。

What does x i.e (x1) signify in the equation?

x ie(x1)在方程式中代表什么？

根據上述相同的方程，x是自變量(IV)，在這里，在簡單線性回歸的情況下，我們只有一個自變量，即x1。 (From the same equation mentioned above, x is the independent variable (IV), here in case of Simple Linear Regression, we have only one independent variable i.e x1.)

This is the variable that is causing the dependent variable to change. From the example mentioned above the years of experience and number of hours spent studying are the independent variables.

這是導致因變量更改的變量。 從上面提到的例子中，多年的經驗和學習時間是自變量。

What does b1 signify in the equation?

b1在方程式中代表什么？

Here, b1 is the coefficient for independent variable i.e x1. This variable(b1) actually decides how a unit change in x1 influences y. Think of it as a multiplier or a connector that connects x and y.

在此，b1是自變量的系數，即x1。 這個變量(b1)實際上決定x1的單位變化如何影響y。 可以將它視為連接x和y的乘法器或連接器。

and then finally comes b0, which is a constant which I will explain in detail in the later section of this article.

然后最后是b0，這是一個常量，我將在本文的后面部分中詳細說明。

ünderstanding SLR與實施例： (Understanding SLR with an Example:)

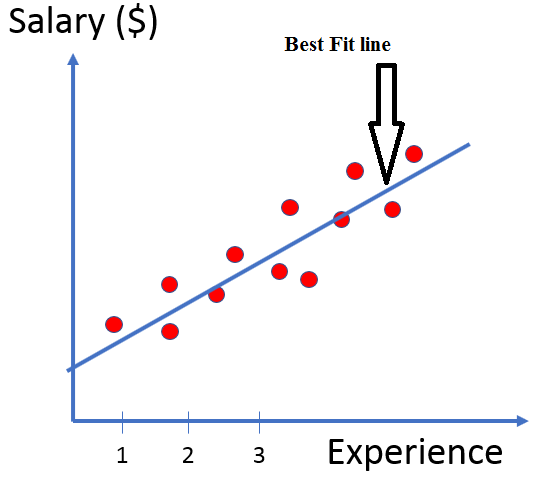
The basic example of Salary vs Years of Experience where Experience (Years of Experience) is in the x-axis and salary is in the y-axis. Our main goal here is to understand how salary is dependent upon the years of experience.Here we have the data of different employees who are working in different companies.

薪金與工作年數的基本示例，其中經驗(年數)在x軸上，薪水在y軸上。 我們的主要目標是了解薪資如何取決于經驗的年限。這里我們擁有在不同公司工作的不同員工的數據。

This is how the Simple Linear Regression formula can be related to the above example:

這就是簡單線性回歸公式與上面的示例相關的方式：

The above formula can be read as Salary equals b zero plus b1 times experience. So what it essentially means is that it is putting a line through the above shown chart that best fits the data. I will explain about the best fitting line as we move ahead when I speak about Ordinary Least Square Method [OLS], but for now as you can see in the below mentioned picture the line that best fits the data.

上面的公式可以理解為薪水等于b零加b1乘以經驗。 因此，這實際上意味著在上面顯示的圖表中劃一條最適合數據的線。 當我談論普通最小二乘法[OLS]時，我將解釋最佳擬合線，但是現在，如下面的圖片所示，您可以看到最適合數據的線。

Let us focus on the coefficients b1 and a constant b0.

讓我們關注系數b1和常數b0。

The constant b0 is the point or value where the line intersects in the vertical axis i.e y-axis. Suppose let’s say b0 value is $30k, so when experience is 0, the second part of the equation i.e b1*experience becomes zero. That means salary = $30k. According to the model when a fresher joins a company his salary will be $30k.

常數b0是線在垂直軸(即y軸)上相交的點或值。 假設b0的值為$ 30k，那么當經驗為0時，等式的第二部分，即b1 * experience變為零。 這意味著薪水= 3萬美元。 根據該模型，當新人加入公司時，他的薪水將為3萬美元。

Now, What is b1?

現在，b1是什么？

b1 is the slope of the line, more money you get as experience increases more will be the value of b1. As you can see in the above image when you perform the projections as per the black dotted lines, for one year increment in the experience there is a increase of around $10k in salary.

b1是直線的斜率，隨著經驗的增加，您獲得的更多金錢將成為b1的價值。 正如您在上圖中所看到的，當按照黑色虛線執行投影時，在一年的經驗積累中，薪水增加了大約1萬美元。

If the coefficient b1 is less, then slope will be less and even the salary increment per year will be less, if the slope is more then the experience will yield more increase in the salary and Yes, that’s how a Simple Linear Regression works.

如果系數b1較小，則斜率將較小，甚至每年的薪金增量也將較小；如果斜率較大，則經驗將使工資增加更多，是的，這就是簡單線性回歸的工作原理。

如何找出簡單線性回歸[SLR]的最佳擬合線？ (How to find out the BEST FIT LINE FOR Simple Linear Regression [SLR]?)

The answer is by Ordinary Least Square[OLS] Method

答案是通過普通最小二乘法[OLS]

Now let’s try to understand how to find out the best fitting line or how SLR finds out that line for us.

現在，讓我們嘗試了解如何找到最佳擬合線，或者SLR如何為我們找到最佳擬合線。

The above shown graph is the same graph which I explained earlier. We have got the red dots that depicts the actual observation, we also have the straight line that best fits the data. To understand the working of OLS method let’s do some modifications on the graph:

上面顯示的圖形與我之前解釋的圖形相同。 我們有描述實際觀察結果的紅點，還有最適合數據的直線。 為了了解OLS方法的工作原理，我們對圖形進行一些修改：

We draw straight lines which are perpendicular to the observations to the best fitting line and then let’s select one observation as shown below:

我們繪制垂直于觀測值的直線到最佳擬合線，然后讓我們選擇一個觀測值，如下所示：

Now you can see from the above picture that the red dot is the salary of a person for a particular year of experience. Let’s assume for 5 years of experience the salary is $50k. The model line, the blue line actually tells us what actually that person should get in terms of salary based on that data in generalized way. Let’s say he should earn $40K for 5 years of experience which is indicated by the green dot on the line.

現在，從上圖可以看到， 紅點是一個人在特定年份的薪水。 假設有5年的工作經驗，工資是$ 50k。 模型行，藍色行實際上告訴我們，根據該數據，該人員應以概括的方式實際獲得的薪水是多少。 假設他應該在5年的經驗中賺到$ 40K，這由行上的綠點表示。

Next, let’s call the red dot as yi that is the actual observation and green dot is called yi^(also called yi hat) which is the observation/value which the model is trying to predict and the blue dotted line is the difference between what the employee is actually earning and what he/she should be earning according to the model. In general, blue dotted line is the difference between the observed and the modeled.

接下來，我們將紅色點稱為yi，這是實際的觀測值，將綠色點稱為yi ^(也稱為yi hat)，這是模型試圖預測的觀測值/值，藍色虛線是兩者之間的差。員工實際賺取的收入以及根據模型應獲得的收入。 通常，藍色虛線是觀察到的和建模之間的差異。

To get this best fitting line, what is done is that we take the sum of (yi-yi^)2, take the value of each one of those dotted blue lines, we square them and then wetake sum of those squares, once we have the sum of those squares we find out the minimum of them.

為了獲得最佳擬合線，要做的是我們取(yi-yi ^)2的總和，取每條虛線藍色線的值，將它們平方，然后取這些平方的和。有那些平方的和，我們找出它們的最小值。

So, what a SLR does is that it draws lots and lots of these lines just like this:

因此，SLR要做的就是繪制很多這樣的線條，如下所示：

and then finds a line which has minimum sum of squares of (yi-yi^) and that line is the best fitting line and the method followed to find out this line is called as the Ordinary least square [OLS] method.

然后找到一條具有(yi-yi ^)的最小平方和的線，并且該線是最佳擬合線，并且為了找出該線而遵循的方法稱為“普通最小二乘[OLS]”方法。

I hope you found this article useful.

希望本文對您有所幫助。

Thank you so much!

非常感謝！

Feel free to connect with me either through LinkedIn, Instagram or Facebook.

隨時通過LinkedIn ， Instagram或Facebook與我聯系。

I will be back with one more exciting article! Till then Stay Safe.

我還會再來一篇精彩的文章！ 直到安全。

Cheers!

干杯!

Arnold Sachith

阿諾德·薩希斯(Arnold Sachith)