邏輯回歸 自由度
Back in middle and high school you likely learned to calculate the mean and standard deviation of a dataset. And your teacher probably told you that there are two kinds of standard deviation: population and sample. The formulas for the two are just small variations on one another:
回到中學和高中時,您可能已經學會了計算數據集的平均值和標準偏差。 您的老師可能告訴過您,標準差有兩種:總體和樣本。 兩者的公式彼此之間只是很小的變化:

where μ is the population mean and x-bar is the sample mean. Typically, one just learns the formulas and is told when to use them. If you ask why, the answer is something vague like “there was one degree of freedom used up when estimating the sample mean.” without a true definition of a “degree of freedom.”
其中,μ是總體平均值,x-bar是樣本平均值。 通常,人們只是學習公式并被告知何時使用它們。 如果您問為什么,答案是模糊的,例如“估計樣本均值時使用了一個自由度。” 沒有“自由度”的真實定義。
Degrees of freedom also show up in several other places in statistics, for example: when doing t-tests, F-tests, χ2 tests, and generally studying regression problems. Depending on the circumstance, degrees of freedom can mean subtly different things (the wikipedia article lists at least 9 closely-related definitions by my count1).
自由度還在統計中的其他幾個地方出現,例如:進行t檢驗,F檢驗,χ2檢驗以及一般研究回歸問題時。 根據情況的不同,自由度可能意味著微妙的不同(根據我的觀點, 維基百科文章列出了至少9個緊密相關的定義1)。
In this article, we’ll focus on the meaning of degrees of freedom in a regression context. Specifically we’ll use the sense in which “degrees of freedom” is the “effective number of parameters” for a model. We’ll see how to compute the number of degrees of freedom of the standard deviation problem above alongside linear regression, ridge regression, and k-nearest neighbors regression. As we go we’ll also briefly discuss the relation to statistical inference (like a t-test) and model selection (how to compare two different models using their effective degrees of freedom).
在本文中,我們將重點介紹回歸上下文中自由度的含義。 具體來說,我們將使用“自由度”是模型的“有效參數數量”的含義。 我們將看到如何在上面與線性回歸,嶺回歸和k最近鄰回歸一起計算標準差問題的自由度數。 在進行過程中,我們還將簡要討論與統計推斷(如t檢驗)和模型選擇(如何使用其有效自由度比較兩個不同模型)的關系。
自由程度 (Degrees of Freedom)
In the regression context we have N samples each with a real-valued outcome value y. For each sample, we have a vector of covariates x, usually taken to include a constant. In other words, the first entry of the x-vector is 1 for each sample. We have some sort of model or procedure (which could be parametric or non-parametric) that is fit to the data (or otherwise uses the data) to produce predictions about what we think the value of y should be given an x-vector (which could be out-of-sample or not).
在回歸上下文中,我們有N個樣本,每個樣本的實值結果值為y 。 對于每個樣本,我們都有一個協變量向量x ,通常將其包括一個常數。 換句話說,對于每個樣本, x向量的第一項均為1。 我們有某種適合數據(或以其他方式使用數據)的模型或過程(可以是參數化的也可以是非參數化的)來產生關于我們認為y值應賦予x向量的預測( (可能超出樣本)。
The result is the predicted value, y-hat, for each of the N samples. We’ll define the degrees of freedom, which we denote as ν (nu):
結果是N個樣本中每個樣本的預測值y-hat。 我們將定義自由度,我們將其表示為ν(nu):

And we’ll interpret the degrees of freedom as the “effective number of parameters” of the model. Now let’s see some examples.
我們將把自由度解釋為模型的“有效參數數量”。 現在讓我們看一些例子。
均值和標準差 (The Mean and Standard Deviation)
Let’s return to the school-age problem we started with. Computing the mean of a sample is just making the prediction that every data point has value equal to the mean (after all, that’s the best guess you can make under the circumstances). In other words:
讓我們回到開始時的學齡問題。 計算樣本均值只是在預測每個數據點的值等于均值(畢竟,這是在這種情況下可以做出的最佳猜測)。 換一種說法:

Note that estimating the mean is equivalent to running a linear regression with only one covariate, a constant: x = [1]. Hopefully this makes it clear why we can re-cast the problem as a prediction problem.
注意,估計均值等效于僅使用一個協變量(常數:x = [1])進行線性回歸。 希望這可以弄清楚為什么我們可以將問題重鑄為預測問題。
Now it’s simple to compute the degrees of freedom. Unsurprisingly we get 1 degree of freedom:
現在,很容易計算自由度。 毫不奇怪,我們獲得了1個自由度:

To understand the relationship to the standard deviation, we have to use another closely related definition of degrees of freedom (which we won’t go into depth on). If our samples were independent and identically distributed, then we can say, informally, that we started out with N degrees of freedom. We lost one in estimating the mean, leaving N–1 left over for the standard deviation.
要了解與標準偏差的關系,我們必須使用另一個密切相關的自由度定義(我們將不對其進行深入介紹)。 如果我們的樣本是獨立的并且分布均勻,那么我們可以非正式地說,我們從N個自由度開始。 我們在估計均值時輸了一個,剩下N-1作為標準差。
香草線性回歸 (Vanilla Linear Regression)
Now let’s expand this into the context of regular old linear regression. In this context, we like to collect the sample data into a vector Y and matrix X. Throughout this article we will use p to denote the number of covariates for each sample (the length of the x-vector).
現在,將其擴展到常規舊線性回歸的上下文中。 在這種情況下,我們希望將樣本數據收集到向量Y和矩陣X中。在整個本文中,我們將使用p表示每個樣本的協變量數( x向量的長度)。
It shouldn’t come as a spoiler that the number of degrees of freedom will end up being p. But the method used to calculate this will pay off for us when we turn to Ridge Regression.
自由度的數量最終將為p不應成為破壞者。 但是,當我們轉向Ridge回歸時,用于計算此費用的方法將為我們帶來回報。
The count of p covariates includes a constant if we include one in our model as we usually do. Each row in the X matrix corresponds to the x-vector for each observation in our sample:
如果我們像往常一樣在模型中加入一個,則p個協變量的計數將包含一個常數。 X矩陣中的每一行對應于樣本中每個觀察值的x-向量:

The model is that there are p parameters collected into a vector β. Y = Xβ plus an error term. We’ll go through the derivation because it will be useful for us later. We pick an estimate for β that minimizes the sum of squares of the errors. In other words our loss function is
該模型是將p個參數收集到向量β中。 Y =Xβ加上誤差項。 我們將進行推導,因為它對以后對我們很有用。 我們為β選擇一個估計,以使誤差平方和最小。 換句話說,我們的損失函數是
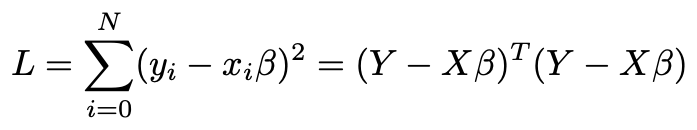
The first sum is in terms of each sample with row-vectors x labeled by i. To optimize L, we differentiate with respect to the vector β, obtaining a p?1 vector of derivatives.
關于每個樣本,第一個和是行向量x標記為i的 。 為了優化L,我們對向量β求微分,得到一個導數為p?1的向量。

Set it equal to 0 and solve for β
將其設置為0并求解β

And finally form our estimate
最后形成我們的估計

We call the matrix H for “hat matrix” because it “puts the hat” on the Y (producing our fitted/predicted values). The hat matrix is an N?N matrix. We are assuming that the y’s are independent, so we can compute the effective degrees of freedom:
我們將矩陣H稱為“帽子矩陣”,因為它“將帽子”放在Y上(產生擬合/預測值)。 帽矩陣是N?N矩陣。 我們假設y是獨立的,因此我們可以計算有效的自由度:

where the second sum is over the diagonal terms in the matrix. If you write out the matrix and write out the formula for the predicted value of sample 1, you will see that these derivatives are in fact just the diagonal entries of the hat matrix. The sum of the diagonals of a matrix is called the Trace of matrix and we have denoted that in the second line.
第二個和在矩陣的對角項上。 如果您寫出矩陣并寫出樣本1的預測值的公式,您會發現這些導數實際上只是帽子矩陣的對角線項。 矩陣對角線的總和稱為跡線 的矩陣,我們已經在第二行指出了這一點。
計算軌跡 (Computing the Trace)
Now we turn to computing the trace of H. We had better hope it is p!
現在我們來計算H的蹤跡。 我們最好希望它是p !
There is a simple way to compute the trace of H using the cyclicality of the trace. But we’ll take another approach that will be generalized when we discuss ridge regression.
有一種使用軌跡的周期性計算H軌跡的簡單方法。 但是,在討論嶺回歸時,我們將采用另一種將被推廣的方法。
We use the singular value decomposition of X. (See my earlier article for a geometric explanation of the singular value decomposition and the linear algebra we are about to do). The trace of a matrix is a basis-independent number, so we can choose whatever basis we want for the vector space containing Y. Similarly, we can choose whatever basis we want for the vector space containing the parameters β. The singular value decomposition says that there exists a basis for each such that the matrix X is diagonal. The entries on the diagonal in the first p rows are called the singular values. The “no perfect multi-collinearity” assumption for linear regression means that none of the singular values are 0. The remaining N–p rows of the matrix are all full of 0s.
我們使用X的奇異值分解 。(有關奇異值分解和線性代數的幾何解釋,請參閱我的較早文章 )。 矩陣的軌跡是一個與基數無關的數,因此我們可以為包含Y的向量空間選擇所需的任何基準。類似地,我們可以為包含參數β的向量空間選擇所需的任何基準。 奇異值分解表示每個矩陣都有一個基礎,使得矩陣X對角線。 前p行中對角線上的條目稱為奇異值 。 線性回歸的“沒有完美的多重共線性”假設意味著奇異值均不為0。矩陣的其余N–p行全為0。
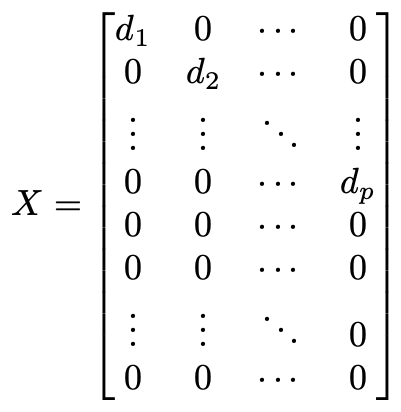
Now it’s easy to compute H. You can just multiply the versions of X by hand and get a diagonal matrix with the first p diagonal entries all 1 and the rest 0. The entries not shown (the off-diagonal ones) are all 0 as well.
現在可以很容易地計算出H。您可以手動乘以X的形式,并得到一個對角矩陣,其中前p個對角線條目均為1,其余為0。未顯示的條目(非對角線條目)全部為0好。

So we conlude Tr(H) = p.
因此我們得出Tr(H)= p的結論。
模擬標準偏差:標準誤差 (Analogue of the Standard Deviation: Standard Error)
In our previous example (mean and standard deviation), we computed the standard deviation after computing the mean, using n–1 for the denominator because we “lost 1 degree of freedom” to estimate the mean.
在前面的示例中(均值和標準差),我們在計算平均值后計算了標準差,對分母使用n-1 ,因為我們“損失了1個自由度”以估算均值。
In this context, the standard deviation gets renamed as the “standard error” but the formula should look analogous:
在這種情況下,標準偏差將重命名為“標準誤差”,但公式??應類似于:

Just as before, we compare the sum of squares of the difference between each measured value y and its predicted value. We used up p degrees of freedom to compute the estimate, so only N–p are left.
和以前一樣,我們比較每個測量值y和其預測值之間的差的平方和。 我們用完了p個自由度來計算估計值,因此只剩下了Np個。
嶺回歸 (Ridge Regression)
In Ridge Regression, we add a regularization term to our loss function. Done properly, this increases bias in our coefficient but decreases variance to result in overall lower error in our predictions.
在Ridge回歸中,我們向損失函數添加一個正則項。 如果做得正確,這會增加我們系數的偏差,但會減少方差,從而使我們的預測總體上降低誤差。
Using our definition of degrees of freedom, we can compute the effective number of parameters in a ridge regression. We would expect the regularization to decrease this below the original number p of parameters (since they no longer freely vary).
使用自由度的定義,我們可以計算嶺回歸中參數的有效數量。 我們期望正則化將其減少到參數的原始數量p以下(因為它們不再自由變化)。
We go through the same steps to compute the hat matrix as in linear regression.
我們采用與線性回歸相同的步驟來計算帽子矩陣。
- The loss function gets an extra term with a fixed, known hyper-parameter λ setting the amount of regularization. 損失函數會得到一個額外的項,其中包含固定的已知超參數λ,用于設置正則化量。

2. We take the derivative, set it equal to 0, and solve for β. I is the identity matrix here
2.我們取導數,將其設置為0,然后求解β。 我是這里的身份矩陣
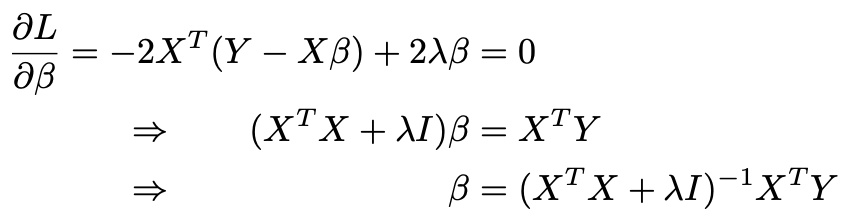
3. We compute the fitted values and extract the hat matrix H. The formula is the same as last time except that we add λ to each diagonal entry of the matrix in parentheses.
3.我們計算擬合值并提取帽子矩陣H。 該公式與上一次相同,只是我們在括號中的矩陣的每個對角線條目中添加了λ。

4. We use the singular value decomposition to choose bases for the vector spaces containing Y and β so that we can write X as a diagonal matrix, and compute H.
4.我們使用奇異值分解為包含Y和β的向量空間選擇基數,以便我們可以將X編寫為對角矩陣,并計算H。

Which leaves us with the following formulas for the degrees of freedom of regular (λ = 0) regression and Ridge regression (λ>0) in terms of the singular values d, indexed by i.
對于正則( d = 0)的正則(λ= 0)回歸和Ridge回歸(λ> 0)的自由度,我們得到以下公式: 由i索引。

討論區 (Discussion)
The above calculations using the singular value decomposition give us a good perspective on Ridge Regression.
以上使用奇異值分解的計算為我們提供了有關嶺回歸的良好視角。
First of all, if the design matrix is perfectly (multi-)collinear, one of its singular values will be 0. A common case where this happens is if there are more covariates than samples. This is a problem in a regular regression because it means the term in parentheses in the hat matrix isn’t invertible (the denominators are 0 in the formula above). Ridge regression fixes this problem by adding a positive term to each squared singular value.
首先,如果設計矩陣是完全(多)共線性的,則其奇異值之一將為0。發生這種情況的一種常見情況是協變量比樣本多。 這是常規回歸中的一個問題,因為這意味著帽子矩陣中括號內的項是不可逆的(上式中的分母為0)。 Ridge回歸通過向每個平方的奇異值添加一個正項來解決此問題。
Second, we can see that the coefficient shrinkage is high for terms with a small singular value. Such terms correspond to components of the β estimate that have high variance in a regular regression (due to high correlation between regressor). On the other hand, for terms with a higher singular value, the shrinkage is comparatively smaller.
其次,我們可以看到奇異值小的項的系數收縮率很高。 這樣的項對應于在常規回歸中具有高方差的β估計值的組成部分(由于回歸變量之間的相關性很高)。 另一方面,對于奇異值較高的項,收縮率相對較小。
The degrees of freedom calculation we have done perfectly encapsulates this shrinkage to give us an estimate for the effective number of parameters we actually used. Note also that the singular values are a function of the design matrix X and not of Y. That means that you could, in theory, choose λ by computing the number of effective parameters you want and finding λ to achieve that.
我們完成的自由度計算完美地封裝了這種收縮,從而可以估算出我們實際使用的有效參數數量。 還要注意,奇異值是設計矩陣X的函數,而不是Y的函數。這意味著從理論上講,您可以通過計算所需的有效參數數量并找到λ來實現這一目的,從而選擇λ。
推論與模型選擇 (Inference and Model Selection)
In our vanilla regression examples we saw that the standard error (or standard deviation) can be computed by assuming that we started with N degrees of freedom and subtracting out the number of effective parameters we used. This doesn’t necessarily make as much sense with the Ridge, which gives a biased estimator for the coefficients (albeit with lower mean-squared error for correctly chosen λ). In particular, the residuals are no longer nicely distributed.
在我們的原始回歸示例中,我們看到可以通過假設我們以N個自由度開始并減去所使用的有效參數的數量來計算標準誤差(或標準差)。 對于Ridge來說,這不一定有意義,因為它為系數提供了一個有偏估計量(盡管正確選擇的λ的均方誤差較低)。 特別是,殘差不再很好地分布。
Instead, we can use our effective number of parameters to plug into the AIC (Akaike Information Criterion), an alternative to cross-validation for model selection. The AIC penalizes models for having more parameters and approximates the expected test error if we were to use a held-out test set. Then choosing λ to optimize it can replace cross-validation, provided we use the effective degrees of freedom in the formula for the AIC. Note, however, that if we choose λ adaptively before computing the AIC, then there are extra effective degrees of freedom added.
相反,我們可以使用有效數量的參數插入AIC (Akaike信息準則),這是模型選擇的交叉驗證的替代方法。 如果我們使用保留的測試集,AIC會對具有更多參數的模型進行懲罰,并近似預期的測試誤差。 如果我們在AIC公式中使用有效自由度,那么選擇λ進行優化可以代替交叉驗證。 但是請注意,如果我們在計算AIC之前自適應地選擇λ,則會增加額外的有效自由度。
K最近鄰回歸 (K-Nearest Neighbors Regression)
As a final example, consider k-nearest neighbors regression. It should be apparent that the fitted value for each data point is the average of k nearby points, including itself. This means that the degrees of freedom is
作為最后一個示例,請考慮k最近鄰回歸。 顯然,每個數據點的擬合值是附近k個點(包括其自身)的平均值。 這意味著自由度是

This enables us to do model comparison between different types of models (for example, comparing k-nearest neighbors to a ridge regression using the AIC as above).
這使我們能夠在不同類型的模型之間進行模型比較(例如,使用上述AIC將k最近鄰與嶺回歸進行比較)。
I hope you see that the degrees of freedom is a very general measure and can be applied to all sorts of regression models (kernel regression, splines, etc.).
我希望您看到自由度是一個非常通用的度量,可以應用于各種回歸模型(內核回歸,樣條曲線等)。
結論 (Conclusion)
Hopefully this article will give you a more solid understanding of degrees of freedom and make the whole concept less of a vague statistical idea. I mentioned that there are other, closely related, definitions of degrees of freedom. The other main version is a geometric idea. If you want to know more about that, read my article about the geometric approach to linear regression. If you want to understand more of the algebra we did to compute the degrees of freedom, read a non-algebraic approach to the singular value decomposition.
希望本文能使您對自由度有更扎實的理解,并使整個概念不再是模糊的統計概念。 我提到過,還有其他與自由度密切相關的定義。 另一個主要版本是幾何構想。 如果您想進一步了解這一點,請閱讀我有關線性回歸的幾何方法的文章。 如果您想了解更多關于代數的知識,我們可以計算自由度,請閱讀有關奇異值分解的非代數方法。
筆記 (Notes)
[1] Specifically I’m counting (a) the geometric definition for a random vector; (b) the closely related degrees of freedom of probability distributions; (c) 4 formulas for the regression degrees of freedom; and (d) 3 formulas for the residual degrees of freedom. You might count differently but will hopefully see my point that there are several closely related ideas and formulas with subtle differences.
[1]具體來說,我是在計算(a)隨機向量的幾何定義; (b)概率分布的自由度密切相關; (c)4個回歸自由度公式; (d)剩余自由度的3個公式。 您可能會有所不同,但希望能看到我的觀點,即有一些密切相關的想法和公式存在細微的差異。
翻譯自: https://towardsdatascience.com/the-official-definition-of-degrees-of-freedom-in-regression-faa04fd3c610
邏輯回歸 自由度
本文來自互聯網用戶投稿,該文觀點僅代表作者本人,不代表本站立場。本站僅提供信息存儲空間服務,不擁有所有權,不承擔相關法律責任。 如若轉載,請注明出處:http://www.pswp.cn/news/391358.shtml 繁體地址,請注明出處:http://hk.pswp.cn/news/391358.shtml 英文地址,請注明出處:http://en.pswp.cn/news/391358.shtml
如若內容造成侵權/違法違規/事實不符,請聯系多彩編程網進行投訴反饋email:809451989@qq.com,一經查實,立即刪除!





 服務器雛形)






 配置文件讀取及連接數據庫)





 TCP/IP 網絡分層以及TCP協議概述)