Machine learning algorithms are not your regular algorithms that we may be used to because they are often described by a combination of some complex statistics and mathematics. Since it is very important to understand the background of any algorithm you want to implement, this could pose a challenge to people with a non-mathematical background as the maths can sap your motivation by slowing you down.

機器學習算法不是我們可能習慣的常規算法，因為它們通常由一些復雜的統計數據和數學的組合來描述。 由于了解要實現的任何算法的背景非常重要，因此這可能會對非數學背景的人構成挑戰，因為數學會通過減慢速度來降低您的動力。

In this article, we would be discussing linear and logistic regression and some regression techniques assuming we all have heard or even learnt about the Linear model in Mathematics class at high school. Hopefully, at the end of the article, the concept would be clearer.

在本文中，我們將討論線性和邏輯回歸以及一些回歸技術，假設我們都已經聽說甚至中學了數學課上的線性模型。 希望在文章末尾，這個概念會更清楚。

Regression Analysis is a statistical process for estimating the relationships between the dependent variables (say Y) and one or more independent variables or predictors (X). It explains the changes in the dependent variables with respect to changes in select predictors. Some major uses for regression analysis are in determining the strength of predictors, forecasting an effect, and trend forecasting. It finds the significant relationship between variables and the impact of predictors on dependent variables. In regression, we fit a curve/line (regression/best fit line) to the data points, such that the differences between the distances of data points from the curve/line are minimized.

回歸分析是一種統計過程，用于估計因變量(例如Y)和一個或多個自變量或預測變量(X)之間的關系 。 它解釋了因變量相對于所選預測變量變化的變化。 回歸分析的一些主要用途是確定預測器的強度，預測效果和趨勢預測。 它發現變量之間的顯著關系以及預測變量對因變量的影響。 在回歸中，我們將曲線/直線(回歸/最佳擬合線)擬合到數據點，以使數據點到曲線/直線的距離之間的差異最小。

線性回歸 (Linear Regression)

It is the simplest and most widely known regression technique. Linear Regression establishes a relationship between the dependent variable (Y) and one or more independent variables (X) using a regression line. This is done by the Ordinary Least-Squares method (OLS calculates the best-fit line for the observed data by minimizing the sum of the squares of the vertical deviations from each data point to the line. Since the deviations are first squared, when added, there is no cancelling out between positive and negative values). It is represented by the equation:

它是最簡單，最廣為人知的回歸技術。 線性回歸使用回歸線在因變量(Y)和一個或多個自變量(X)之間建立關系。 這是通過普通最小二乘方法完成的 (OLS通過最小化每個數據點到該行的垂直偏差的平方和來計算觀測數據的最佳擬合線。 ，則無法在正值和負值之間抵消)。 它由等式表示：

Y=a+b*X + e; where a is intercept, b is slope of the line and e is error term.

Y = a + b * X + e; 其中a是截距，b是直線的斜率，e是誤差項。

The OLS has several assumptions. They are-

OLS有幾個假設。 他們是-

1. Linearity: The relationship between X and the mean of Y is linear.

   線性 ：X和Y的平均值之間的關系是線性的。

2. Normality: The error(residuals) follow a normal distribution.

   正態性 ：誤差(殘差)服從正態分布。

3. Homoscedasticity: The variance of residual is the same for any value of X (Constant variance of errors).

   均 方差性：對于任何X值，殘差方差都是相同的(誤差的方差恒定)。

4. No Endogeneity of regressors: It refers to the prohibition of a link between the independent variables and the errors

   回歸變量無內生性 ：指禁止自變量與錯誤之間的聯系

5. No autocorrelation: Errors are assumed to be uncorrelated and randomly spread across the regression line.

   無自相關 ：假定錯誤是不相關的，并且隨機分布在回歸線上。

6. Independence/No multicollinearity: it is observed when two or more variables have a high correlation.

   獨立/無多重共線性：當兩個或多個變量具有高度相關性時，會觀察到。

We have simple and multiple linear regression, the difference being that multiple linear regression has more than one independent variables, whereas simple linear regression has only one independent variable.

我們有簡單和多元線性回歸，區別在于多元線性回歸具有多個自變量，而簡單線性回歸只有一個自變量。

We can evaluate the performance of this model using the metric R-square.

我們可以使用度量R平方來評估此模型的性能。

邏輯回歸 (Logistic Regression)

Using linear regression, we can predict the price a customer will pay if he/she buys. With logistic regression we can make a more fundamental decision, “will the customer buy at all?”

使用線性回歸，我們可以預測客戶購買時將支付的價格。 通過邏輯回歸，我們可以做出更基本的決定，“客戶是否愿意購買？”

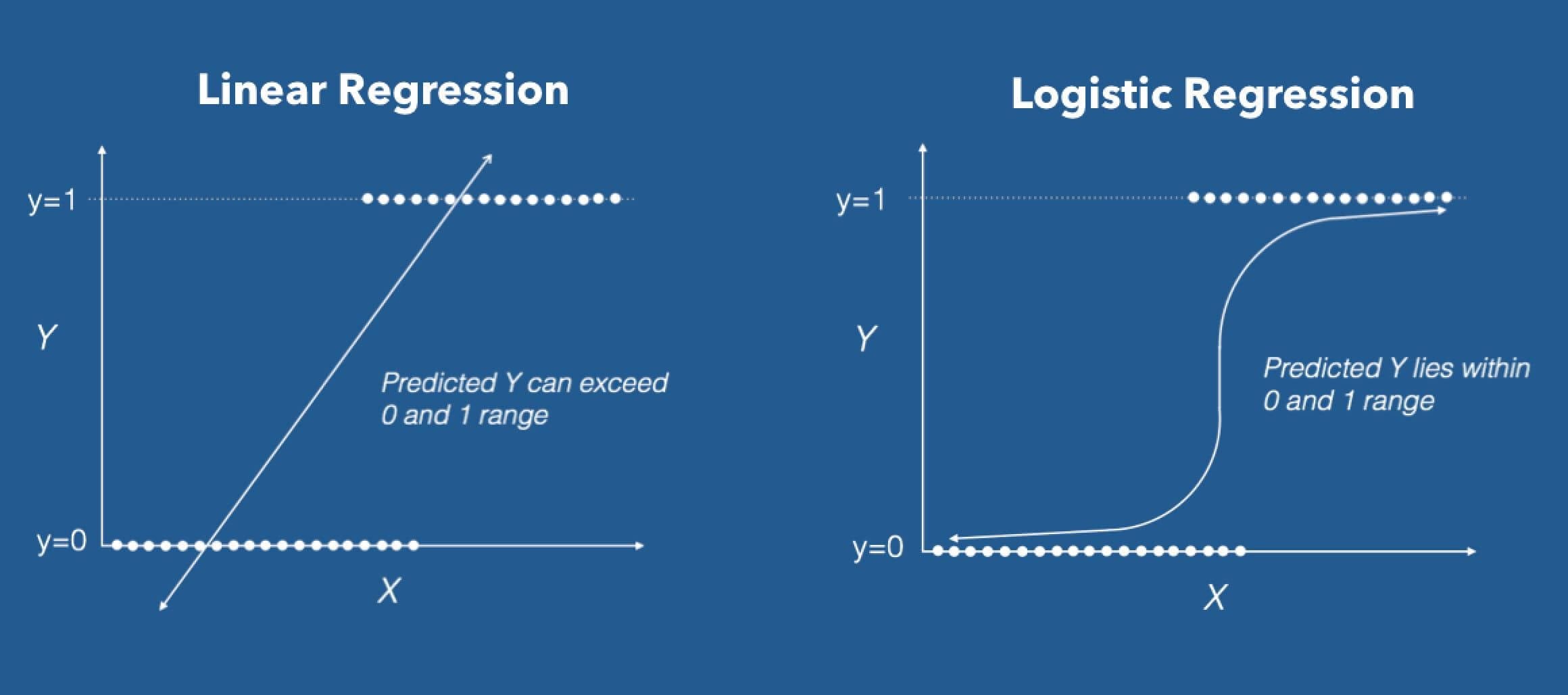
Here, there is a shift from numerical to categorical. It is used in solving classification problems and in prediction where our targets are categorical variables. It can handle various types of relationships between the independent variables and Y because it applies a non-linear log transformation to the predicted odds ratio.

在這里，從數字到絕對是一個轉變。 它用于解決分類問題和預測，其中我們的目標是分類變量。 它可以處理自變量和Y之間的各種類型的關系，因為它將非線性對數轉換應用于預測的優勢比。

odds= p/ (1-p) ln(odds) = ln(p/(1-p))logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3….+bkXk

賠率= p /(1-p)ln(奇數)= ln(p /(1-p))logit(p)= ln(p /(1-p))= b0 + b1X1 + b2X2 + b3X3…。+ bkXk

where p is the probability of event success and (1-p) is the probability of event failure.

其中p是事件成功的概率，而(1-p)是事件失敗的概率。

The logit function can map any real value between 0 and 1. The parameters in the equation above are chosen to maximize the likelihood of observing the sample values rather than minimizing the sum of squared errors.

logit函數可以映射0到1之間的任何實數值。選擇上式中的參數是為了最大化觀察樣本值的可能性，而不是最小化平方誤差的總和。

結論。 (Conclusion.)

I would encourage you to read further to get a more solid understanding. There are several techniques employed in increasing the robustness of regression. They include regularization/penalisation methods(Lasso, Ridge and ElasticNet), gradient descent, stepwise regression, and so on.

我鼓勵您進一步閱讀以獲得更扎實的理解。 有幾種技術可以提高回歸的魯棒性。 它們包括正則化/懲罰化方法(Lasso，Ridge和ElasticNet)，梯度下降，逐步回歸等。

Kindly note that they are not types of regression as was noticed in many articles online. Below, you will find links to articles I found helpful in explaining some concepts and for your further reading. Happy learning!

請注意，它們不是許多在線文章所注意到的回歸類型。 在下面，您會找到指向我的文章的鏈接，這些文章對我解釋一些概念和進一步閱讀很有幫助。 學習愉快！

https://medium.com/datadriveninvestor/regression-in-machine-learning-296caae933ec

https://medium.com/datadriveninvestor/regression-in-machine-learning-296caae933ec

https://machinelearningmastery.com/linear-regression-for-machine-learning/

https://machinelearningmastery.com/linear-regression-for-machine-learning/

https://www.geeksforgeeks.org/ml-linear-regression/

https://www.geeksforgeeks.org/ml-linear-regression/

https://www.geeksforgeeks.org/types-of-regression-techniques/

https://www.geeksforgeeks.org/types-of-regression-techniques/

https://www.vebuso.com/2020/02/linear-to-logistic-regression-explained-step-by-step/

https://www.vebuso.com/2020/02/linear-to-logistic-regression-explained-step-by-step/

https://www.statisticssolutions.com/what-is-logistic-regression/

https://www.statisticssolutions.com/what-is-logistic-regression/

https://www.listendata.com/2014/11/difference-between-linear-regression.html#:~:text=Purpose%20%3A%20Linear%20regression%20is%20used,the%20probability%20of%20an%20event.

https://www.listendata.com/2014/11/difference-between-linear-regression.html#:~:text=Purpose%20%3A%20Linear%20regression%20is%20used,%20probability%20of%20an ％20event 。

https://www.kaggle.com/residentmario/l1-norms-versus-l2-norms

https://www.kaggle.com/residentmario/l1-norms-versus-l2-norms