給你一個用無限二維網格表示的花園，每一個 整數坐標處都有一棵蘋果樹。整數坐標 (i, j) 處的蘋果樹有 |i| + |j| 個蘋果。
你將會買下正中心坐標是 (0, 0) 的一塊 正方形土地 ，且每條邊都與兩條坐標軸之一平行。
給你一個整數 neededApples ，請你返回土地的 最小周長 ，使得 至少 有 neededApples 個蘋果在土地 里面或者邊緣上。
|x| 的值定義為：
如果 x >= 0 ，那么值為 x
如果 x < 0 ，那么值為 -x
示例 1：
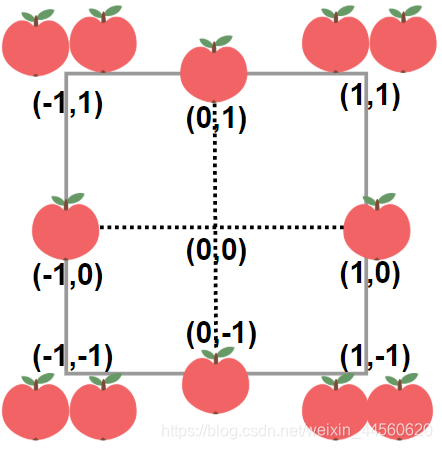
輸入：neededApples = 1
輸出：8
解釋：邊長長度為 1 的正方形不包含任何蘋果。
但是邊長為 2 的正方形包含 12 個蘋果（如上圖所示）。
周長為 2 * 4 = 8 。
示例 2：
輸入：neededApples = 13
輸出：16
示例 3：
輸入：neededApples = 1000000000
輸出：5040
解題思路
將蘋果樹分為若干層，每一層蘋果的數量都可以由上一層推出
公式為：wp+=point+12+82weight
- wp代表蘋果的個數
- weight代表當前層數
- point代表上一層的點數
代碼
class Solution {public long minimumPerimeter(long neededApples) {long point=8,weight=1,pre=12,z=2,wp=12;while (neededApples>pre){wp+=point+12+8*2*weight;pre+=wp;point+=8;weight++;}return weight*8;}
}
