223. 矩形面積

給你 二維 平面上兩個 由直線構成的 矩形，請你計算并返回兩個矩形覆蓋的總面積。

每個矩形由其 左下 頂點和 右上 頂點坐標表示：

第一個矩形由其左下頂點 (ax1, ay1) 和右上頂點 (ax2, ay2) 定義。
第二個矩形由其左下頂點 (bx1, by1) 和右上頂點 (bx2, by2) 定義。

示例 1：

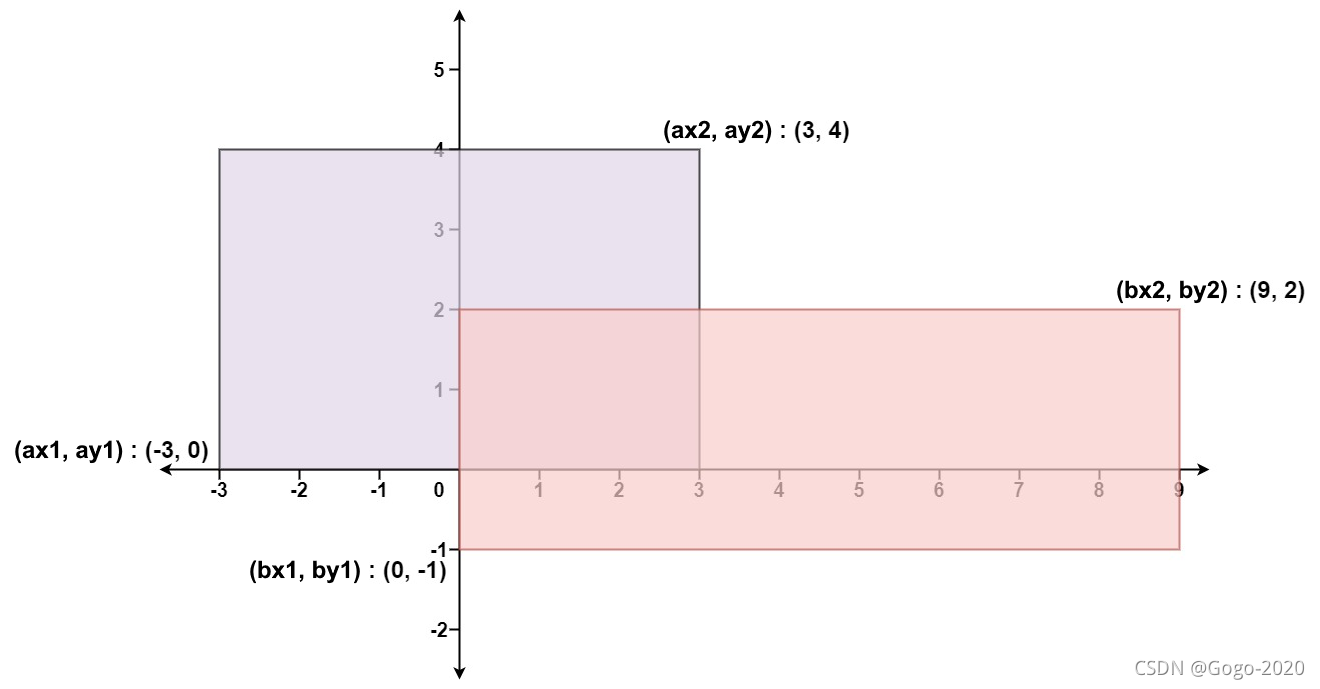
輸入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
輸出：45
示例 2：

輸入：ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
輸出：16

解題思路

矩形的面積由兩種情況產生

1. 兩個矩形不相交
   只需各自計算兩個矩形的面積，然后加起來

兩個矩形不相交的條件為：by1>=ay2||by2<=ay1||bx1>=ax2||ax1>=bx2

2. 兩個矩形相交
   計算兩個矩形重疊的面積，然后再在兩個矩形的總面積中減去重疊部分的

重疊部分的面積公式：(Math.min(by2,ay2)-Math.max(by1,ay1))* (Math.min(bx2,ax2)-Math.max(bx1,ax1))

代碼

class Solution {public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {int sum=(ay2-ay1)*(ax2-ax1)+(by2-by1)*(bx2-bx1);if(by1>=ay2||by2<=ay1||bx1>=ax2||ax1>=bx2)return sum;return sum-(Math.min(by2,ay2)-Math.max(by1,ay1))* (Math.min(bx2,ax2)-Math.max(bx1,ax1));}
}