The Linear Regression is the simplest non-trivial relationship. The biggest mistake one can make is to perform a regression analysis that violates one of its assumptions! So, it is important to consider these assumptions before applying regression analysis on the dataset.

線性回歸是最簡單的非平凡關系。 一個人可能犯的最大錯誤是進行違反其假設之一的回歸分析！ 因此，在對數據集進行回歸分析之前，必須考慮這些假設。

This article focuses both on the assumptions and measures to fix them in case the dataset violates it.

本文著重于假設和糾正假設的方法，以防數據集違反假設。

1. Linearity: The specified model must represent a linear relationship.

   線性：指定的模型必須表示線性關系。

This is the simplest assumption to deal with as it signifies that the relationship between dependent and independent variable is linear wherein independent variable is multiplied by its coefficient to obtain dependent variable.

這是要處理的最簡單假設，因為它表示因變量和自變量之間的關系是線性的，其中將自變量乘以其系數即可獲得因變量。

Y=β0?+β1X1?+…+βkXk+ε

Y =β0 +β1X1 + ... +βKXK +ε

It is quite easy to verify this assumption as plotting independent variable against dependent variable on a scatterplot gives us insights whether the pattern formed can be represented through a line or not. However, applying linear regression on data would not be appropriate if a line can’t fit the data. In the latter case, one can perform non-linear regression, logarithmic or exponential transformation on the dataset to convert it into a linear relationship.

驗證這一假設非常容易，因為在散點圖上繪制自變量與因變量的關系使我們洞悉所形成的模式是否可以通過線條表示。 但是，如果一條線無法擬合數據，則對數據進行線性回歸將是不合適的。 在后一種情況下，可以對數據集執行非線性回歸，對數或指數變換，以將其轉換為線性關系。

2. No endogeneity of regressors: The independent variables shouldn’t be correlated with the error term.

2. 回歸變量無內生性：自變量不應與誤差項相關。

This refers to the prohibition of link between the independent variable and the error term. Mathematically, it can be expressed in the following way.

這是指禁止自變量與錯誤項之間的鏈接。 在數學上，它可以用以下方式表示。

𝜎 𝑥,𝜀 =0:?𝑥,𝜀

𝜎 𝜀，𝜀 = 0：?𝑥，𝜀

As we know that independent variables involved in the model are somewhat correlated. The incorrect exclusion of one or more independent variable that could be relevant for the model gives us the omitted variable bias. This excluded variable ultimately gets reflected in the error term resulting in the covariance between the independent variable and the error term as non zero.

眾所周知，模型中涉及的自變量有些相關。 錯誤地排除可能與模型相關的一個或多個自變量會給我們省略變量偏差。 該排除的變量最終反映在誤差項中，導致自變量和誤差項之間的協方差為非零。

The only way to deal with this assumption is to try different variables for the model so as to ensure that relevant variables are very well conisdered in the model.

處理此假設的唯一方法是為模型嘗試不同的變量，以確保在模型中很好地考慮了相關變量。

3. Normality and Homoscedasticity: The variance of the errors should be consistent across observations.

3. 正態性和同方性：誤差的方差在所有觀測值之間應保持一致。

This assumption states that the error term is normally distributed and an expected value (mean) is zero. It is important to note that normal distribution of the term is only required for making inferences.

該假設表明誤差項為正態分布，期望值(均值)為零。 重要的是要注意，僅在進行推斷時才需要該術語的正態分布。

𝜀 ~𝑁 (0,𝜎2)

𝜀?𝑁(0，𝜎2)

As far as homoscedasticity is concerned, it simply means variance of all error terms related to independent variables is equal to each other. However, below is an example of a dataset with different variance of the error terms. The regression performed on this dataset would have a better result for smaller values of independent and dependent variables.

就同??質性而言，它僅表示與自變量相關的所有誤差項的方差彼此相等。 但是，以下是誤差項的方差不同的數據集的示例。 對于較小的自變量和因變量，對該數據集執行的回歸將具有更好的結果。

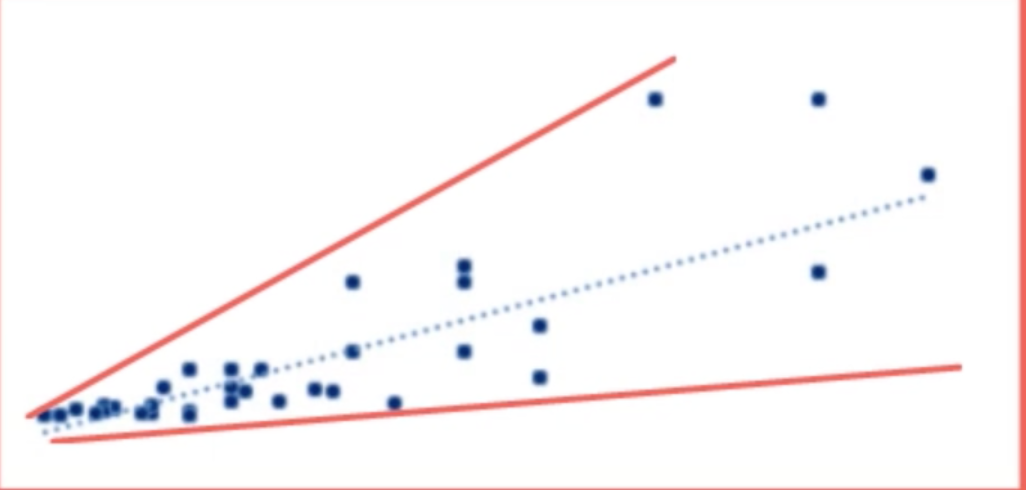
The way forward to validate this assumption is to look for omitted variable bias, outliers and perform log transformation.

驗證該假設的方法是尋找遺漏的變量偏差，離群值并執行對數轉換。

4. No Autocorrelation: No identifiable relationship should exist between the values of the error term

4. 無自相關：誤差項的值之間不應存在可識別的關系

This assumption is the least favorite of all as it is hard to fix. Mathematically, it is represented in the following way.

該假設是所有假設中最不喜歡的，因為它很難解決。 在數學上，它以以下方式表示。

𝜎 𝜀𝑖𝜀𝑗=0:?𝑖 ≠𝑗

𝜎 𝜀𝑖𝜀𝑗 = 0：?𝑖≠𝑗

It is assumed that error terms are un-correlated. A common way to identify this is Durbin-Watson test which is provided in the regression summary table. If the value is less than one or more than three, it indicates autocorrelation. If the value is 2, there is no autocorrelation. It is better to avoid linear regression when there is autocorrelation.

假定誤差項是不相關的。 識別此問題的常用方法是回歸匯總表中提供的Durbin-Watson檢驗。 如果該值小于一或大于三，則表示自相關。 如果值為2，則不存在自相關。 自相關時最好避免線性回歸。

5. No Multicollinearity: No predictor variable should be perfectly (or almost perfectly) explained by the other predictors.

5.沒有多重共線性：其他預測變量不能完美(或幾乎完美)地解釋預測變量。

It is observed when two or more variables have high correlation. The logic behind this assumption is that if two variables have high collinearity, there is no point of representing both the variables in the model .

當兩個或多個變量具有高相關性時可以觀察到。 該假設背后的邏輯是，如果兩個變量具有較高的共線性，則沒有必要在模型中表示兩個變量。

𝜌 𝑥𝑖𝑥𝑗 ?1:?𝑖,𝑗; 𝑖 ≠𝑗

?1：?𝑖，𝑗; 𝑖≠𝑗

It is easy to validate this assumption by dropping one of the variable or transforming them into one.

通過刪除變量之一或將其轉換為一個變量可以很容易地驗證這一假設。

Criticisms/suggestions are really welcome 🙂.

批評/建議真的很受歡迎🙂。