k最近鄰居 (k-Nearest Neighbors)

k-Nearest Neighbors (KNN) is a supervised machine learning algorithm that can be used for either regression or classification tasks. KNN is non-parametric, which means that the algorithm does not make assumptions about the underlying distributions of the data. This is in contrast to a technique like linear regression, which is parametric, and requires us to find a function that describes the relationship between dependent and independent variables.

k最近鄰(KNN)是一種受監督的機器學習算法，可用于回歸或分類任務。 KNN是非參數的，這意味著該算法不對數據的基礎分布進行假設。 這與參數化的線性回歸等技術形成對比，后者是參數化的，要求我們找到一個描述因變量和自變量之間關系的函數。

KNN has the advantage of being quite intuitive to understand. When used for classification, a query point (or test point) is classified based on the k labeled training points that are closest to that query point.

KNN具有非常直觀易懂的優點。 當用于分類時，根據最接近該查詢點的k個標記訓練點對查詢點(或測試點)進行分類。

For a simplified example, see the figure below. The left panel shows a 2-d plot of sixteen data points — eight are labeled as green, and eight are labeled as purple. Now, the right panel shows how we would classify a new point (the black cross), using KNN when k=3. We find the three closest points, and count up how many ‘votes’ each color has within those three points. In this case, two of the three points are purple — so, the black cross will be labeled as purple.

有關簡化示例，請參見下圖。 左面板顯示了16個數據點的二維圖-八個標記為綠色，八個標記為紫色。 現在，右面板顯示了當k = 3時，如何使用KNN對新點(黑色十字)進行分類。 我們找到三個最接近的點，并計算出每種顏色在這三個點內有多少個“票數”。 在這種情況下，三個點中的兩個是紫色的-因此，黑色十字將被標記為紫色。

Calculating Distance

計算距離

The distance between points is determined by using one of several versions of the Minkowski distance equation. The generalized formula for Minkowski distance can be represented as follows:

點之間的距離是通過使用Minkowski距離方程的幾個版本之一確定的。 Minkowski距離的廣義公式可以表示為：

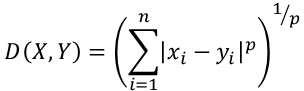
where X and Y are data points, n is the number of dimensions, and p is the Minkowski power parameter. When p =1, the distance is known at the Manhattan (or Taxicab) distance, and when p=2 the distance is known as the Euclidean distance. In two dimensions, the Manhattan and Euclidean distances between two points are easy to visualize (see the graph below), however at higher orders of p, the Minkowski distance becomes more abstract.

其中X和Y是數據點， n是維數， p是Minkowski冪參數。 當p = 1時，該距離已知為曼哈頓(或出租車)距離，而當p = 2時，該距離稱為歐幾里得距離。 在兩個維度上，兩點之間的曼哈頓距離和歐幾里得距離很容易可視化(請參見下圖)，但是在p的高階處，明可夫斯基距離變得更加抽象。

Python中的KNN (KNN in Python)

To implement my own version of the KNN classifier in Python, I’ll first want to import a few common libraries to help out.

為了用Python實現我自己的KNN分類器版本，我首先要導入一些常見的庫來提供幫助。

# Initial importsimport pandas as pd
import numpy as np
import matplotlib.pyplot as plt

加載數據中 (Loading Data)

To test the KNN classifier, I’m going to use the iris data set from sklearn.datasets. The data set has measurements (Sepal Length, Sepal Width, Petal Length, Petal Width) for 150 iris plants, split evenly among three species (0 = setosa, 1 = versicolor, and 2 = virginica). Below, I load the data and store it in a dataframe.

為了測試KNN分類器，我將使用sklearn.datasets中的虹膜數據集。 數據集具有150種鳶尾植物的測量值(頭長，萼片寬度，花瓣長度，花瓣寬度)，均勻地分為三種(0 =剛毛，1 =雜色和2 =弗吉尼亞)。 在下面，我加載數據并將其存儲在數據框中。

# Load iris data and store in dataframefrom sklearn import datasetsiris = datasets.load_iris()df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['target'] = iris.target
df.head()

I’ll also separate the data into features (X) and the target variable (y), which is the species label for each plant.

我還將數據分為特征(X)和目標變量(y)，目標變量是每種植物的種類標簽。

# Separate X and y dataX = df.drop('target', axis=1)
y = df.target

建立KNN框架 (Building out the KNN Framework)

Creating a functioning KNN classifier can be broken down into several steps. While KNN includes a bit more nuance than this, here’s my bare-bones to-do list:

創建功能良好的KNN分類器可以分為幾個步驟。 盡管KNN包含的細微之處要多于此，但以下是我的基本工作清單：

1. Define a function to calculate the distance between two points
   定義一個函數來計算兩點之間的距離
2. Use the distance function to get the distance between a test point and all known data points
   使用距離函數獲取測試點與所有已知數據點之間的距離
3. Sort distance measurements to find the points closest to the test point (i.e., find the nearest neighbors)
   對距離測量值進行排序，以找到最接近測試點的點(即，找到最近的鄰居)
4. Use majority class labels of those closest points to predict the label of the test point
   使用那些最接近的點的多數類標簽來預測測試點的標簽
5. Repeat steps 1 through 4 until all test data points are classified
   重復步驟1至4，直到對所有測試數據點進行分類

1.定義一個函數來計算兩點之間的距離 (1. Define a function to calculate distance between two points)

First, I define a function called minkowski_distance, that takes an input of two data points (a & b) and a Minkowski power parameter p, and returns the distance between the two points. Note that this function calculates distance exactly like the Minkowski formula I mentioned earlier. By making p an adjustable parameter, I can decide whether I want to calculate Manhattan distance (p=1), Euclidean distance (p=2), or some higher order of the Minkowski distance.

首先，我定義一個名為minkowski_distance的函數，該函數接受兩個數據點( a ＆ b )和一個Minkowski冪參數p的輸入，并返回兩個點之間的距離。 請注意，此函數計算距離的方式與我之前提到的Minkowski公式完全相同。 通過將p設置為可調參數，我可以決定是否要計算曼哈頓距離(p = 1)，歐幾里得距離(p = 2)或Minkowski距離的更高階。

# Calculate distance between two pointsdef minkowski_distance(a, b, p=1):# Store the number of dimensionsdim = len(a)# Set initial distance to 0distance = 0# Calculate minkowski distance using parameter pfor d in range(dim):distance += abs(a[d] - b[d])**pdistance = distance**(1/p)return distance# Test the functionminkowski_distance(a=X.iloc[0], b=X.iloc[1], p=1)

0.6999999999999993

2.使用距離功能獲取測試點與所有已知數據點之間的距離 (2. Use the distance function to get distance between a test point and all known data points)

For step 2, I simply repeat the minkowski_distance calculation for all labeled points in X and store them in a dataframe.

對于第2步，我只需要對X中所有標記的點重復minkowski_distance計算，并將它們存儲在數據框中。

# Define an arbitrary test pointtest_pt = [4.8, 2.7, 2.5, 0.7]# Calculate distance between test_pt and all points in Xdistances = []for i in X.index:distances.append(minkowski_distance(test_pt, X.iloc[i]))df_dists = pd.DataFrame(data=distances, index=X.index, columns=['dist'])
df_dists.head()

3.對距離測量值進行排序以找到最接近測試點的點 (3. Sort distance measurements to find the points closest to the test point)

In step 3, I use the pandas .sort_values() method to sort by distance, and return only the top 5 results.

在第3步中，我使用pandas .sort_values()方法按距離排序，并且僅返回前5個結果。

# Find the 5 nearest neighborsdf_nn = df_dists.sort_values(by=['dist'], axis=0)[:5]
df_nn

4.使用那些最近點的多數類標簽來預測測試點的標簽 (4. Use majority class labels of those closest points to predict the label of the test point)

For this step, I use collections.Counter to keep track of the labels that coincide with the nearest neighbor points. I then use the .most_common() method to return the most commonly occurring label. Note: if there is a tie between two or more labels for the title of “most common” label, the one that was first encountered by the Counter() object will be the one that gets returned.

對于這一步，我使用collections.Counter來跟蹤與最近的鄰居點重合的標簽。 然后，我使用.most_common()方法返回最常見的標簽。 注意：如果兩個或兩個以上標簽之間的關系為“最常見”標簽的標題，則Counter()對象首先遇到的標簽將是返回的標簽。

from collections import Counter# Create counter object to track the labelscounter = Counter(y[df_nn.index])# Get most common label of all the nearest neighborscounter.most_common()[0][0]

1

5.重復步驟1至4，直到對所有測試數據點進行分類 (5. Repeat steps 1 through 4 until all test data points are classified)

In this step, I put the code I’ve already written to work and write a function to classify the data using KNN. First, I perform a train_test_split on the data (75% train, 25% test), and then scale the data using StandardScaler(). Since KNN is distance-based, it is important to make sure that the features are scaled properly before feeding them into the algorithm.

在這一步中，我將已經編寫的代碼投入使用，并編寫了一個使用KNN對數據進行分類的函數。 首先，我對數據執行train_test_split (75％的火車，25％的測試)，然后使用StandardScaler()縮放數據。 由于KNN是基于距離的，因此在將特征輸入算法之前，確保正確縮放特征很重要。

Additionally, to avoid data leakage, it is good practice to scale the features after the train_test_split has been performed. First, scale the data from the training set only (scaler.fit_transform(X_train)), and then use that information to scale the test set (scaler.tranform(X_test)). This way, I can ensure that no information outside of the training data is used to create the model.

此外，為避免數據泄漏，優良作法是在train_test_split執行之后縮放功能。 首先，僅縮放訓練集中的數據 ( scaler.fit_transform(X_train) )，然后使用該信息來縮放測試集( scaler.tranform(X_test) )。 這樣，我可以確保沒有使用訓練數據之外的任何信息來創建模型。

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler# Split the data - 75% train, 25% testX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25,random_state=1)# Scale the X datascaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

Next, I define a function called knn_predict that takes in all of the training and test data, k, and p, and returns the predictions my KNN classifier makes for the test set (y_hat_test). This function doesn’t really include anything new — it is simply applying what I’ve already worked through above. The function should return a list of label predictions containing only 0’s, 1’s and 2’s.

接下來，我定義一個名為knn_predict的函數，該函數接收所有訓練和測試數據k和p ，并返回我的KNN分類器對測試集所做的預測( y_hat_test )。 該功能實際上并沒有包含任何新功能-只是應用了我上面已經完成的工作。 該函數應返回僅包含0、1和2的標簽預測列表。

def knn_predict(X_train, X_test, y_train, y_test, k, p):# Counter to help with label votingfrom collections import Counter# Make predictions on the test data# Need output of 1 prediction per test data pointy_hat_test = []for test_point in X_test:distances = []for train_point in X_train:distance = minkowski_distance(test_point, train_point, p=p)distances.append(distance)# Store distances in a dataframedf_dists = pd.DataFrame(data=distances, columns=['dist'], index=y_train.index)# Sort distances, and only consider the k closest pointsdf_nn = df_dists.sort_values(by=['dist'], axis=0)[:k]# Create counter object to track the labels of k closest neighborscounter = Counter(y_train[df_nn.index])# Get most common label of all the nearest neighborsprediction = counter.most_common()[0][0]# Append prediction to output listy_hat_test.append(prediction)return y_hat_test# Make predictions on test dataset
y_hat_test = knn_predict(X_train, X_test, y_train, y_test, k=5, p=1)print(y_hat_test)

[0, 1, 1, 0, 2, 1, 2, 0, 0, 2, 1, 0, 2, 1, 1, 0, 1, 1, 0, 0, 1, 1, 2, 0, 2, 1, 0, 0, 1, 2, 1, 2, 1, 2, 2, 0, 1, 0]

And there they are! These are the predictions that this home-brewed KNN classifier has made on the test set. Let’s see how well it worked:

在那里！ 這些是這個自制的KNN分類器對測試集所做的預測。 讓我們看看它的效果如何：

# Get test accuracy scorefrom sklearn.metrics import accuracy_scoreprint(accuracy_score(y_test, y_hat_test))

0.9736842105263158

Looks like the classifier achieved 97% accuracy on the test set. Not too bad at all! But how do I know if it actually worked correctly? Let’s check the result of sklearn’s KNeighborsClassifier on the same data:

看起來分類器在測試集上達到了97％的準確性。 一點也不差！ 但是我怎么知道它是否真的正常工作呢？ 讓我們在相同數據上檢查sklearn的KNeighborsClassifier的結果：

# Testing to see results from sklearn.neighbors.KNeighborsClassifierfrom sklearn.neighbors import KNeighborsClassifierclf = KNeighborsClassifier(n_neighbors=5, p=1)
clf.fit(X_train, y_train)
y_pred_test = clf.predict(X_test)print(f"Sklearn KNN Accuracy: {accuracy_score(y_test, y_pred_test)}")

Sklearn KNN Accuracy: 0.9736842105263158

Nice! sklearn’s implementation of the KNN classifier gives us the exact same accuracy score.

真好！ sklearn對KNN分類器的實現為我們提供了完全相同的準確性得分。

探索變化k的影響 (Exploring the effect of varying k)

My KNN classifier performed quite well with the selected value of k = 5. KNN doesn’t have as many tune-able parameters as other algorithms like Decision Trees or Random Forests, but k happens to be one of them. Let’s see how the classification accuracy changes when I vary k:

我的KNN分類器在選定的k = 5時表現很好。KNN沒有像決策樹或隨機森林之類的其他算法那么多的可調參數，但k恰好是其中之一。 讓我們看看改變k時分類精度如何變化：

# Obtain accuracy score varying k from 1 to 99accuracies = []for k in range(1,100):y_hat_test = knn_predict(X_train, X_test, y_train, y_test, k, p=1)accuracies.append(accuracy_score(y_test, y_hat_test))# Plot the results fig, ax = plt.subplots(figsize=(8,6))
ax.plot(range(1,100), accuracies)
ax.set_xlabel('# of Nearest Neighbors (k)')
ax.set_ylabel('Accuracy (%)');

In this case, using nearly any k value less than 20 results in great (>95%) classification accuracy on the test set. However, when k becomes greater than about 60, accuracy really starts to drop off. This makes sense, because the data set only has 150 observations — when k is that high, the classifier is probably considering labeled training data points that are way too far from the test points.

在這種情況下，幾乎使用任何小于20的k值，都可以在測試集上實現較高的分類精度(> 95％)。 但是，當k大于約60時，精度實際上開始下降。 這是有道理的，因為數據集只有150個觀察值-當k很高時，分類器可能正在考慮與測試點相距太遠的標記訓練數據點。

每個鄰居都有投票權嗎？ (Every neighbor gets a vote — or do they?)

In writing my own KNN classifier, I chose to overlook one clear hyperparameter tuning opportunity: the weight that each of the k nearest points has in classifying a point. In sklearn’s KNeighborsClassifier, this is the weights parameter, and it can be set to ‘uniform’, ‘distance’, or another user-defined function.

在編寫自己的KNN分類器時，我選擇忽略了一個明確的超參數調整機會： k個最近點中的每一個在對點進行分類時所具有的權重。 在sklearn的KNeighborsClassifier中 ，這是weights參數，可以將其設置為'uniform' ， 'distance'或其他用戶定義的函數。

When set to ‘uniform’, each of the k nearest neighbors gets an equal vote in labeling a new point. When set to ‘distance’, the neighbors in closest to the new point are weighted more heavily than the neighbors farther away. There are certainly cases where weighting by ‘distance’ would produce better results, and the only way to find out is through hyperparameter tuning.

當設置為'uniform'時 ，k個最近的鄰居中的每一個在標記新點時都會得到平等的投票。 設置為“距離”時 ，最接近新點的鄰居的權重要比更遠的鄰居的權重大。 當然，在某些情況下，按“距離”進行加權會產生更好的結果，唯一的找出方法是通過超參數調整。

最后的想法 (Final Thoughts)

Now, make no mistake — sklearn’s implementation is undoubtedly more efficient and more user-friendly than what I’ve cobbled together here. However, I found it a valuable exercise to work through KNN from ‘scratch’, and it has only solidified my understanding of the algorithm. I hope it did the same for you!

現在，請不要誤解-sklearn的實現無疑比我在這里拼湊的實現更加有效和用戶友好。 但是，我發現從“從頭開始”通過KNN進行工作是一個有價值的練習，并且它僅鞏固了我對算法的理解。 希望對您也一樣！