To study structure,tear away all flesh soonly the bone shows.

要研究結構，請盡快撕掉骨頭上所有的肉。

Linear algebra. Graph theory. If you are a data scientist, you have encountered both of these fields in your study or work at some point. They are part of a standard curriculum, frequently used tools in the kit of every engineer.

線性代數。 圖論。 如果您是數據科學家，則在研究或工作中有時會遇到這兩個領域。 它們是標準課程的一部分，是每個工程師工具包中常用的工具。

What is rarely taught, however, is that they have a very close and fruitful relationship. Graphs can be used to prove strong structural results about matrices easily and beautifully.

但是，很少有人教給他們，他們之間的關系非常密切而富有成果。 圖可以用來輕松，美觀地證明矩陣的強大結構結果。

To begin our journey, first, we shall take a look at how a matrix can be described with a graph.

首先，我們將看看如何用圖形描述矩陣。

矩陣作為圖 (Matrices as graphs)

Suppose that we have a square matrix

假設我們有一個方矩陣

We say that the weighted and directed graph

我們說加權有向圖

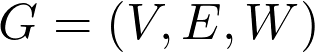
corresponds to A if

對應于A，如果

If this sounds complicated, here is an example.

如果這聽起來很復雜，請舉一個例子。

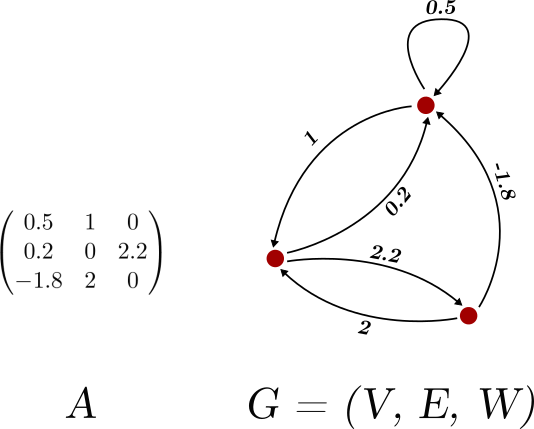
So, for every square matrix, we have a weighted and directed graph. In general, having distinct representations for the same object is colossally useful in mathematics. Sometimes, complex things can be significantly simplified the moment you start looking at things from a different perspective.

因此，對于每個方陣，我們都有一個加權有向圖。 通常，對于同一對象具有不同的表示形式在數學中非常有用。 有時，從開始以不同的角度看待事物時，復雜的事物就可以大大簡化。

Such as the case of matrices and graphs.

例如矩陣和圖形的情況。

在圖上走動 (Walking around the graph)

A great feature of the graph representation is the ability to visualize matrix powers.

圖形表示的一個很大的特點是可視化矩陣冪的能力。

Suppose that the k-th power of A is denoted by

假設A的k次冪表示為

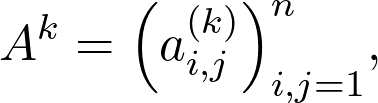
where k can be any positive integer. For k = 2, it is calculated by

其中k可以是任何正整數。 對于k = 2 ，其計算公式為

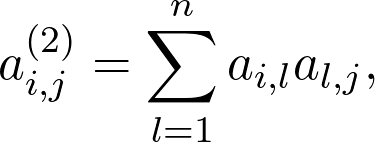
which seems pretty mystical.

這似乎很神秘。

With graphs, there is a pretty simple explanation.

對于圖形，有一個非常簡單的解釋。

For any two nodes i and j, there are several ways to go from one to another. These are called walks. In general, a walk is defined by the sequence of vertices

對于任何兩個節點i和j ，有幾種方法可以從一個轉移到另一個。 這些被稱為步行 。 通常，走行由頂點序列定義

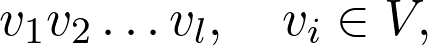
where there must be an edge between v? and v???. Since the graph of the matrix is weighted, we can define the weight of the walk as well by multiplying the weights of each edge traversed:

在v?和v???之間必須有一條邊。 由于矩陣的圖形是加權的，因此我們也可以通過將遍歷的每個邊的權重相乘來定義步行的權重：

(To motivate the definition, let’s suppose we are talking about a transition graph of a discrete Markov chain. In this case, the weight of a walk would equal to the probability of having consecutive states corresponding to the prescribed walk.)

(為激發定義，讓我們假設我們正在談論離散馬爾可夫鏈的轉移圖。在這種情況下，步行的權重將等于具有對應于規定步行的連續狀態的概率。)

So, in graph terminology,

因此，在圖形術語中，

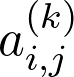
equals to the sum of weights for all possible k-long paths between i and j. This is easy to see for k = 2, and the general case follows from this using induction.

等于i和j之間所有可能的k長路徑的權重之和。 對于k = 2來說 ，這很容易看到，并且一般情況是通過歸納法得出的。

混合起來(字面意思) (Mixing things up (literally))

If you are familiar with some advanced topics in linear algebra, you must have encountered the concept of similar matrices. A and B are called similar if there is a matrix P such that

如果您熟悉線性代數的一些高級主題，那么您一定已經遇到過類似矩陣的概念。 如果存在一個矩陣P使得A和B 相似

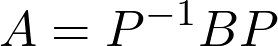
holds. This is a very important concept. If we think of matrices as linear transformations, similarity means that A and B are essentially the same transformations, only in a different coordinate system. (And P is the change of coordinates.)

持有。 這是一個非常重要的概念。 如果我們將矩陣視為線性變換，則相似性意味著A和B本質上是相同的變換，只是在不同的坐標系中。 ( P是坐標的變化。)

For example, some matrices can be diagonalized with similarity transformations. So, if we look at them using a special coordinate system, a complicated matrix may just describe a simple stretching.

例如，某些矩陣可以通過相似性變換進行對角化。 因此，如果我們使用特殊的坐標系查看它們，則復雜的矩陣可能只是描述了簡單的拉伸。

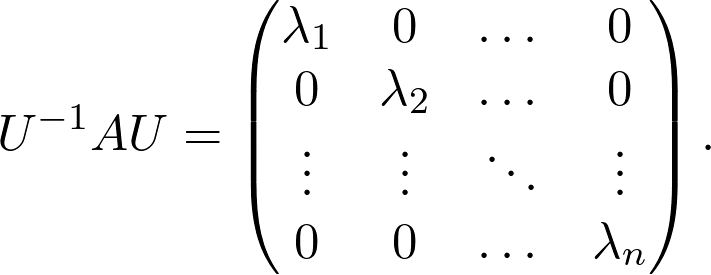
An important special case is where the similarity matrix P is a so-called permutation matrix.

一個重要的特殊情況是，相似矩陣P是所謂的置換矩陣 。

置換矩陣 (Permutation matrices)

In mathematics, any bijective mapping

在數學中，任何雙射映射

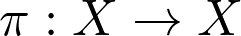
is called a permutation. Specifically, if X = {1, 2, …, n}, then π is simply a reordering of the numbers.

稱為排列。 具體來說，如果X = {1,2，…，n} ，則π只是數字的重新排序。

Any such permutation can be represented with a matrix, defined by

任何這樣的排列都可以用一個矩陣表示，該矩陣由

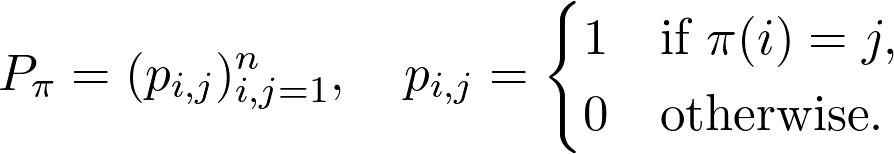
If this is not easy to understand, no worries, I’ll give an example right now. For the permutation defined by

如果這不容易理解，不用擔心，我現在就舉一個例子。 對于由定義的排列

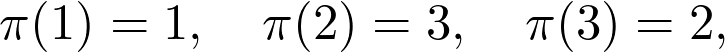
we have

我們有

Why do we define the permutation matrix this way? To see this, consider the following:

為什么我們用這種方式定義置換矩陣？ 要看到這一點，請考慮以下因素：

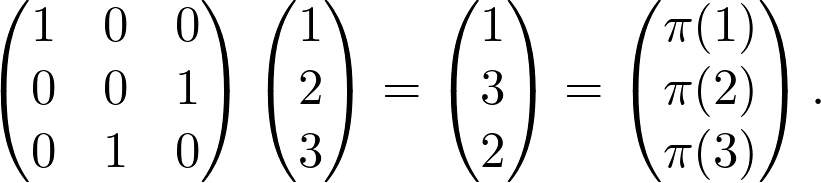
Multiplying a matrix with a permutation matrix shuffles its rows or columns, depending on whether we multiply from the left or right, so we have

將矩陣與置換矩陣相乘會改變其行或列，具體取決于我們是從左側還是右側進行乘法運算，因此

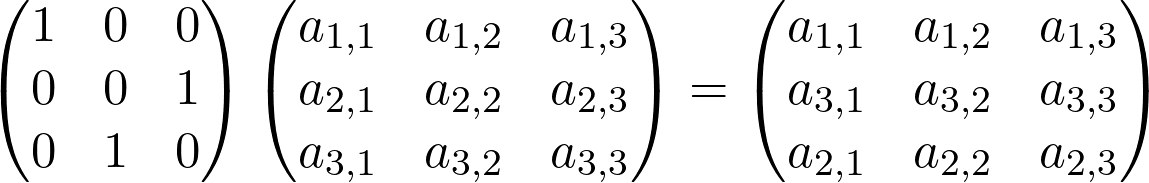
and

和

(Recall that matrix multiplication is not commutative.)

(回想一下，矩陣乘法不是可交換的。)

The inverse of a permutation matrix is its transpose. This is easy to see, once you explicitly calculate the product

置換矩陣的逆是它的轉置。 一旦您明確計算出乘積，這很容易看到

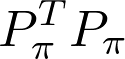
by hand.

用手。

置換矩陣的相似性變換 (Similarity transforms with permutation matrices)

So, let’s go back to graphs and matrices. For a given permutation matrix and a matrix A, what does the similarity transform do? If you think about it, the matrix

因此，讓我們回到圖和矩陣。 對于給定的置換矩陣和矩陣A ，相似度變換做什么？ 如果您考慮一下，矩陣

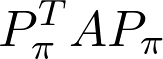
contains identical elements, just its rows and columns are shuffled. In fact, their corresponding graphs are isomorphic with each other. (Which is a fancy expression for being the same after relabeling certain vertices.) Although showing this might look difficult, it can be done by simply noting three key things.

包含相同的元素，只是其行和列被改組。 實際上，它們對應的圖彼此同構。 (在重新標注某些頂點后，這是一個很好的表達方式，因為它是相同的。)盡管顯示這一點看起來很困難，但可以通過簡單地注意三個關鍵事項來完成。

• The graph of APπ can be obtained from the graph of A by taking all edges (i, j) and replacing them with (i, π(j)).

  通過取所有邊(i，j)并將其替換為(i，π(j))可以從A的圖獲得APπ的圖。

• Similarly, the graph of Pπ?A can be obtained by replacing (i, j) with

  類似地，可以通過將(i，j)替換為Pπ?A的圖

  Similarly, the graph of Pπ?A can be obtained by replacing (i, j) with (π?1(i), j ).

  類似地，可以通過用(π11(i)，j)代替(i，j)來獲得Pπ?A的圖。

• Every permutation graph can be written as a product of permutation matrices where only two elements are swapped. These are called transpositions and their inverses are themselves.

  每個排列圖都可以寫成僅交換兩個元素的排列矩陣的乘積。 這些被稱為換位 ，它們的逆本身。

矩陣的結構 (The structure of matrices)

A central question in the theory of matrices is to simplify and reveal their underlying structure by some kind of transformation, like similarity.

矩陣理論中的一個中心問題是通過某種轉換(例如相似性)來簡化和揭示其基本結構。

For example, as mentioned, certain matrices can be diagonalized by a similarity transformation:

例如，如前所述，某些矩陣可以通過相似性變換進行對角化：

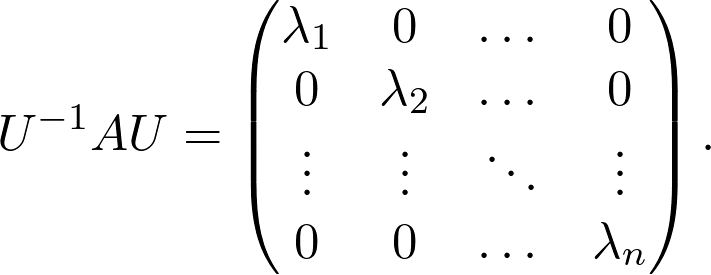
Note that this is not true for all matrices. (Check out the spectral theorem if you are interested.) Diagonal matrices are special and easy to work with, so when diagonalization is possible, our job is much simpler.

請注意，并非所有矩陣都是如此。 ( 如果您有興趣，請查看頻譜定理。 )對角矩陣是特殊的并且易于使用，因此，在可能進行對角化的情況下，我們的工作會簡單得多。

Another special form is the block-triangular form. The matrix A is upper block-triangular, if there are submatrices B, C, D such that

另一個特殊形式是塊三角形形式。 如果存在子矩陣B，C，D ，則矩陣A為上塊三角形

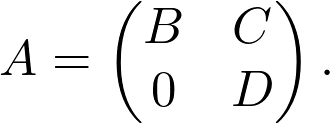
(Note that 0 is a matrix with all zeros here.)

(請注意， 0是此處為全零的矩陣。)

Definition. A nonnegative matrix A is called reducible, if it can be upper block-triangularized with a similarity transform using a permutation matrix P:

定義。 如果非負矩陣A可以使用置換矩陣P進行相似度變換并進行上塊三角化，則稱為可約矩陣A ：

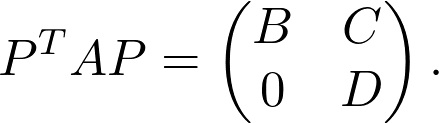
If it cannot be done, the matrix is called irreducible. From a graph-theoretical perspective, reducibility is equivalent to partitioning the nodes to two subsets S, T such that there are no outgoing edges from T to S.

如果無法完成，則將矩陣稱為不可約 。 從圖論的角度來看，可簡化性等效于將節點劃分為兩個子集S，T ，這樣就沒有從T到S的傳出邊。

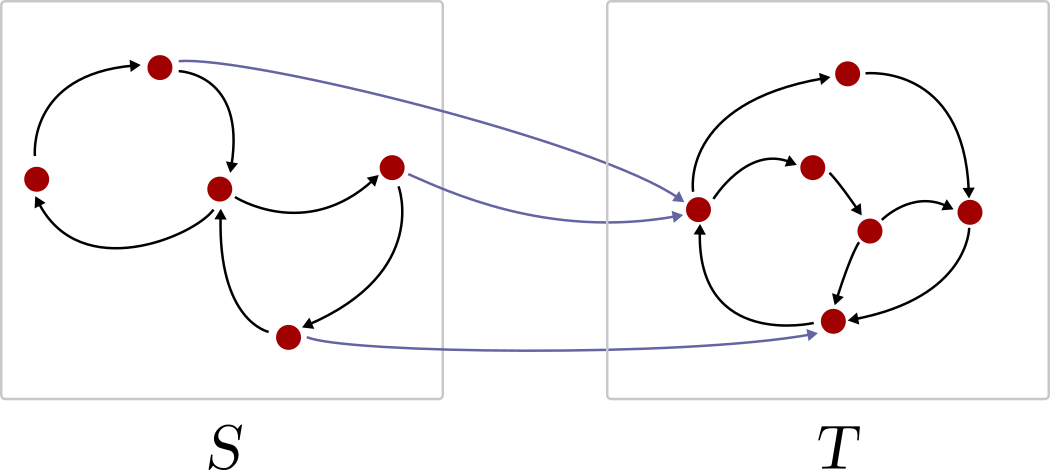
Imagine that you are randomly walking along the edges of this graph, like a Markov chain. Reducibility means that once you enter T, you cannot leave it. (And, if there is a nonzero probability to enter, you will enter eventually.)

想象一下，您像Markov鏈一樣隨機地沿著該圖的邊緣行走。 可簡化性意味著，一旦輸入T ，就無法離開它。 (并且，如果輸入的可能性非零， 則最終將輸入 。)

With irreducible and reducible matrices, nonnegative matrices can be significantly simplified, as we shall see next.

使用不可約矩陣和可約矩陣，可以顯著簡化非負矩陣，這將在后面看到。

Frobenius范式 (The Frobenius normal form)

Before going into explanations, let’s just state the theorem.

在進行解釋之前，讓我們先陳述定理。

Theorem. (Frobenius normal form) For every nonnegative matrix A, there is a permutation matrix P such that

定理。 (Frobenius范式)對于每個非負矩陣A ，都有一個置換矩陣P使得

where the A? -s are irreducible matrices.

其中A?- s是不可約矩陣。

This theorem is hard to prove using only the tools of algebra. (As it was done originally.) However, with graphs, it is almost trivial.

僅使用代數工具很難證明該定理。 (正如最初所做的那樣。)但是，對于圖形來說，這幾乎是微不足道的。

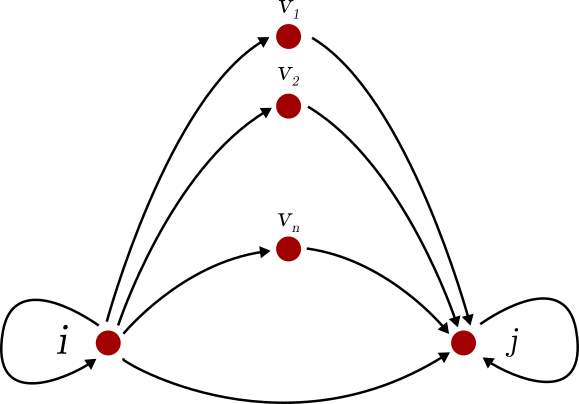
To do this, let’s introduce the concept of strongly connectedness nodes in the graph. The nodes i and j are strongly connected if there is a directed walk from i to j AND a directed walk from j to i. That is, they are mutually reachable from each other.

為此，讓我們在圖中介紹強連接節點的概念。 如果存在從i到j的定向走和從j到i的定向走，則節點i和j是牢固連接的。 即，它們彼此可以相互到達。

In the language of algebra, the relation “i and j are strongly connected” is an equivalence relation. This means that they partition V into subsets V?, V?, …, V? such that all vertices in V? are strongly connected, but NOT strongly connected with any other vertex.

用代數的語言來說，關系“ i和j緊密相連”是等價關系。 這意味著它們劃分V輸入子集V 1，V 2，...，V?使得V?所有頂點是密切聯系的，但與其他任何頂點非強連接。

For illustration, the graph looks something like this.

為了說明，該圖看起來像這樣。

Believe it or not, this proves the Frobenius theorem about the normal form. To see, we just have to renumber the vertices such that each strongly connected set of vertices are numbered consecutively. As we have seen, the renumbering of vertices is equivalent to applying a permutation transform. Hence,

信不信由你，這證明了Frobenius定理關于正規形式。 要看到，我們只需要對頂點重新編號，以使每個強連接的頂點集都被連續編號。 如我們所見，頂點的重編號等效于應用置換變換。 因此，

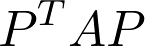
is of the desired form.

具有所需的形式。

This theorem illustrates the use of graph theory in linear algebra. By simply drawing a picture, so many structural patterns are revealed.

該定理說明了圖論在線性代數中的使用。 通過簡單地繪制圖片，可以顯示出許多結構模式。

Of course, this is just the tip of the iceberg. If you are interested, check out the book A Combinatorial Approach to Matrix Theory and Its Applications by Richard A. Brualdi and Dragos Cvetkovic, which is full of beautiful mathematics regarding this topic.

當然，這只是冰山一角。 如果您有興趣，請閱讀Richard A. Brualdi和Dragos Cvetkovic撰寫的《矩陣理論及其應用的組合方法 》一書，其中充斥著與此主題相關的精美數學知識。

結論 (Conclusion)

Graphs and matrices go hand in hand. Specifically, graph theory provides a new way to think about matrices. Although this is usually not part of a standard curriculum in linear algebra, it is a fruitful connection between the two. With it, certain structural aspects of matrices become trivial.

圖形和矩陣齊頭并進。 具體來說，圖論提供了一種思考矩陣的新方法。 盡管這通常不是線性代數標準課程的一部分，但這是兩者之間卓有成效的聯系。 有了它，矩陣的某些結構方面變得無關緊要。