背景 (Background)

In Kaggle’s M5 Forecasting — Accuracy competition, the square root transformation ruined many of my team’s forecasts and led to a selective patching effort in the eleventh hour. Although it turned out well, we were reminded that “reconstitution bias” can plague predictions on the original scale, even with common transformations such as the square root.

在Kaggle的“ M5預測-準確性”競賽中 ，平方根轉換破壞了我團隊的許多預測，并在第11小時進行了選擇性修補工作。 盡管結果很好 ，但我們仍被提醒，“重構偏見”會困擾原始規模的預測，即使采用平方根之類的常見轉換也是如此。

平方根變換 (The square root transformation)

For Poisson data, the rationale of the square root is that it is a variance-stabilizing transformation; in theory, the square root of the values are distributed approximately normal with constant variance and a mean that is the square root of the original mean. It is an approximation, and as Wikipedia puts it, one in which the “convergence to normality (as [the original mean] increases) is far faster than the untransformed variable.”

對于Poisson數據 ，平方根的基本原理是它是方差穩定的變換； 從理論上講，值的平方根近似分布，且具有恒定方差，且均值是原始均值的平方根。 正如Wikipedia所說 ，這是一種近似，其中“ 歸一化的收斂性(隨著(原始均值)的增加)比未轉換的變量快得多。 ”

Imagine you decide to take square roots in a count data scenario, feeling good reassured that the convergence to normality is “fast.” You then model the mean of square-root transformed data and then get predictions on the square root scale. At some point, especially in a forecasting scenario, you’ll have to get back to the original scale. That probably entails squaring the model-estimated means. The M5 competition served as a reminder that this approach can and will break down.

想象一下，您決定在計數數據方案中求平方根，并確信向正態的收斂是“快速的”。 然后，您可以對平方根轉換后的數據的均值建模，然后獲得平方根尺度的預測。 在某些時候，尤其是在預測情況下，您必須回到原始比例。 這可能需要對模型估計的均方進行平方。 M5競賽提醒我們，這種方法可能并且將會失敗。

詹森差距 (The Jensen Gap)

Jensen’s Inequality states that for convex functions, the function evaluated at the expectation is less than or equal to the expectation of the function, i.e., g(E[Y]) ≤ E[g(Y)]. The inequality is flipped for concave functions.

Jensen不等式指出，對于凸函數，按期望評估的函數小于或等于該函數的期望，即g(E [Y])≤E [g(Y)]。 對于凹函數，不等式被翻轉。

Similarly, the Jensen Gap is defined as the difference E[g(Y)]-g(E[Y]), which is positive for convex functions g. (As an aside, notice that when g(x) is the square function, the Jensen Gap is the Variance of Y, which had better be non-negative!)

類似地， 詹森差距定義為差E [ g ( Y )]- g (E [ Y ])，對于凸函數g為正。 (順便說一句， 請注意，當g ( x )是平方函數時，Jensen Gap 是 Y的方差，最好是非負的！)

When considering g(x) as the square function and the square root of Y as the random variable, the Jensen Gap becomes E[Y]-E[sqrt(Y)]2. Since that quantity is positive, our reconstituted mean will be biased downward. To learn more about the magnitude of the gap, we turn to the Taylor expansion.

當將g ( x )作為平方函數并將Y的 平方根作為隨機變量時，Jensen Gap變為E [ Y ] -E [sqrt( Y )]2。 由于該數量為正，因此我們重構的均值將向下偏向。 要了解有關差距大小的更多信息，我們轉向泰勒展開。

泰勒展開至近似偏差 (Taylor expansion to approximate bias)

To the Mathematics StackExchange prompt “Expected Value of Square Root of Poisson Random Variable,” contributor Hernan Gonzalez explains the Taylor expansion of a random variable about its mean, as shown in the screenshot below.

在數學StackExchange提示“ 泊松隨機變量平方根的期望值 ”中， 貢獻者Hernan Gonzalez解釋了隨機變量的泰勒展開式及其均值，如下面的屏幕快照所示。

Note that the expansion needs at least a few central moments of the original distribution. For the Poisson, the first three are just the mean parameter.

請注意，展開至少需要原始分布的幾個中心時刻。 對于泊松而言，前三個只是均值參數。

Ignoring that the mean estimator is also a random variable, we can run the expectation above through the inverse transformation, i.e., square it, to get an idea of the bias on the original scale for any Poisson mean value (the algebra isn’t here but it’s computed in line 34 of the demonstration code.) Similarly, with properties of the square root of the random variable, it’s straightforward to analyze g(x) = x ^2 in the same way. That opens up the possibility of bias correction, an interesting proposition, albeit one with assumptions and complexities of its own.

忽略均值估計器也是一個隨機變量，我們可以通過逆變換在上面運行期望值，即對它求平方，以了解任何泊松均值在原始比例上的偏差(代數不在此處但是，它是在演示代碼的第34行中計算出來的 。)類似地，由于具有隨機變量的平方根的屬性，因此以相同的方式分析g (x)= x ^ 2很簡單。 這開辟了偏差校正的可能性，這是一個有趣的主張，盡管它有其自身的假設和復雜性。

近似分解 (Approximation breakdown)

Near the end of his answer, Gonzalez mentions that the approximation “is only useful if” the mean of the original Poisson is quite a bit bigger than 1, clarifying in the comments that this is needed so that “the terms of the sum decrease quickly.” That follows from the mean being raised to negative powers after the original term.

岡薩雷斯在回答接近尾聲時提到，“ 僅當 ”原始泊松的均值比1大很多時，近似值“ 才有用 ”，并在注釋中闡明了這一點是必要的，以便“ 總和的項Swift減少”。 。 ”這是因為原任期之后，均值被提升為負數。

In the M5 competition, mean sales for many items were substantially below one, and thus using the square root transformation was a recipe for poor performance. To get an idea of how this plays out in an actual sample, the next section will investigate this phenomenon via simulation.

在M5競賽中，許多商品的平均銷售額都大大低于1，因此使用平方根變換是降低性能的良方。 為了了解這種情況在實際樣本中如何發揮作用，下一部分將通過仿真研究這種現象。

示范 (Demonstration)

In this section, we use the loess smoother to create models on both the original scale and the square root scale, and square the mean estimates of the latter. For simulated Poisson data with both a mean of 20 and a mean of 0.2, we plot the two sets of predictions and examine the bias. The code is under 50 lines and is available in Nousot’s Public Github repository.

在本節中，我們將使用黃土平滑器在原始比例和平方根比例上創建模型，并對后者的均值進行平方。 對于均值為20和均值為0.2的模擬Poisson數據，我們繪制了兩組預測并檢查了偏差。 該代碼少于50行，可在Nousot的Public Github存儲庫中找到 。

當平均值是20 (When the mean is 20)

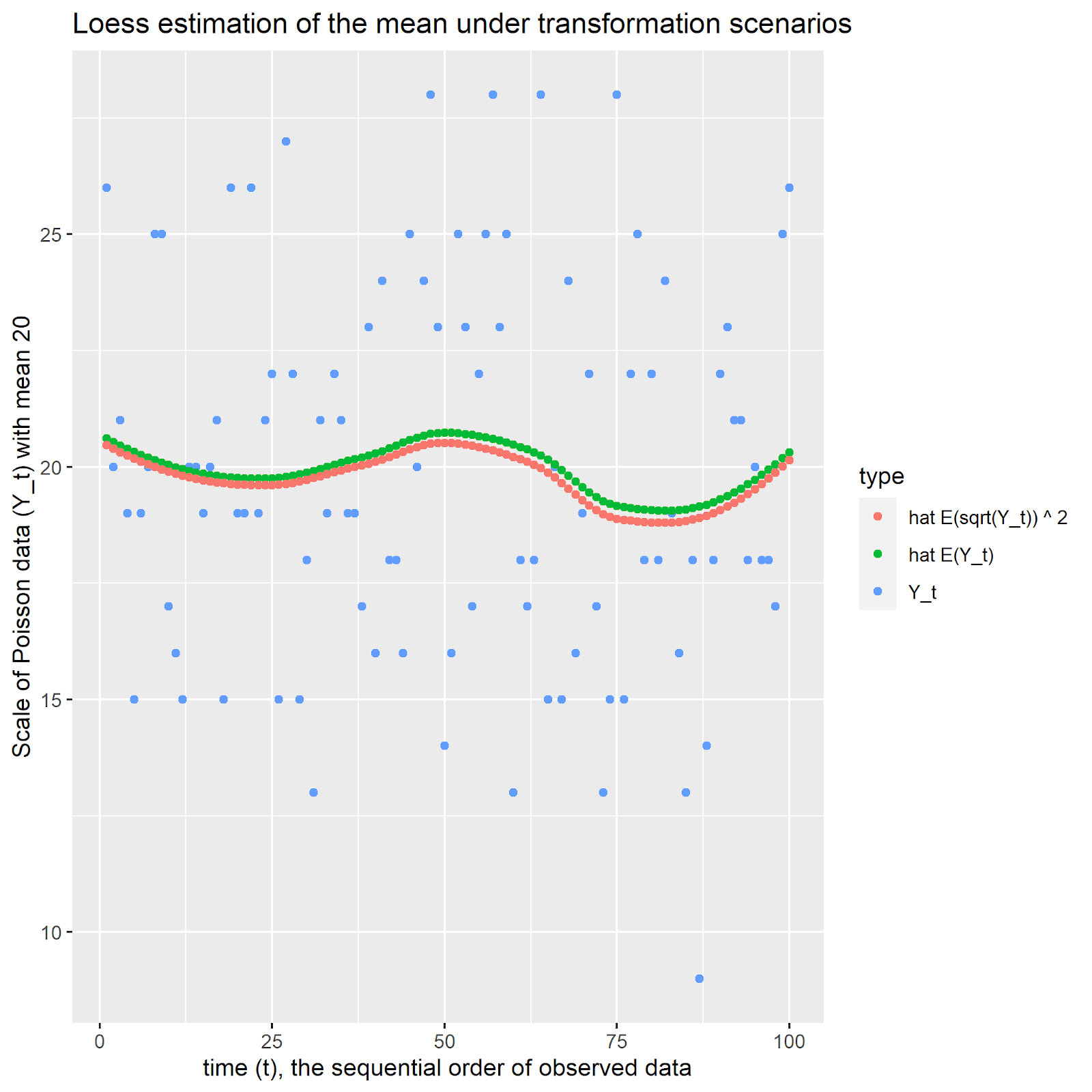
For the case where the mean of the Poisson random variable is 20, the retransformation bias is negative (as Jensen’s Inequality said it would be), but also relatively small. In the code, the first two terms of the Taylor expansion are computed and compared to the empirical bias on the square root scale. At -0.027 and -0.023, respectively, they are relatively close.

對于泊松隨機變量的平均值為20的情況，重變換偏差為負(就像詹森的不等式所說的那樣)，但也相對較小。 在代碼中，計算出泰勒展開的前兩個項，并將其與平方根尺度上的經驗偏差進行比較。 它們分別為-0.027和-0.023，相對接近。

當平均值為0.20時 (When the mean is 0.20)

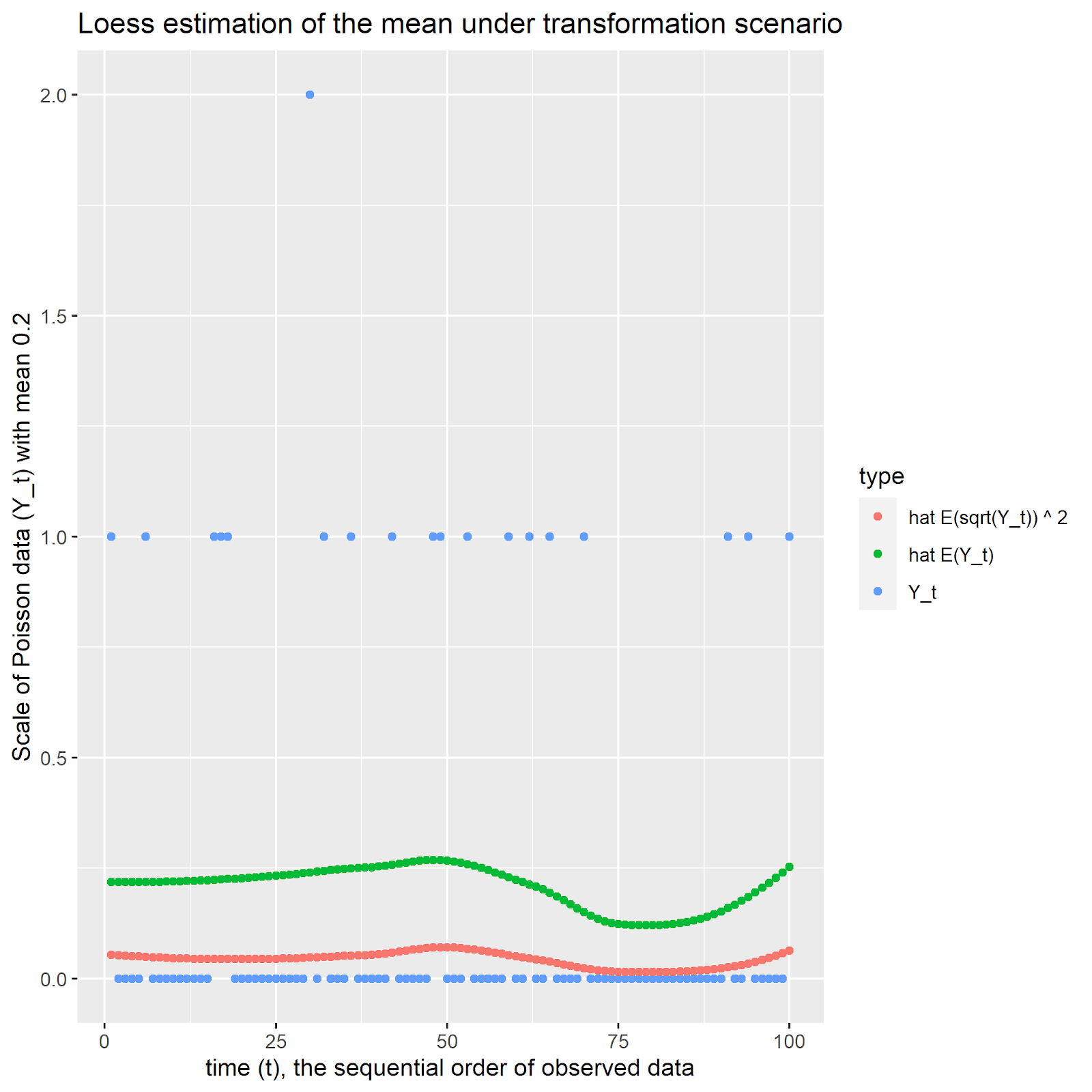
For the case where the mean of the Poisson random variable is 0.20, the picture is much different. While Jensen’s Inequality always holds, the Jensen Gap is now large in a relative sense. Furthermore, the Taylor approximation has completely broken down, with the first two bias terms summing to 0.419 while the empirical bias is -.251 (still on the square root scale).

對于泊松隨機變量的平均值為0.20的情況，圖片有很大不同。 盡管詹森的不平等現象始終存在，但詹森差距現在相對來說還是很大的。 此外，泰勒近似已完全分解，前兩個偏差項的總和為0.419，而經驗偏差為-.251(仍在平方根刻度上)。

討論區 (Discussion)

David Warton’s 2018 paper “Why You Cannot Transform Your Way Out of Trouble for Small Counts” demonstrates the hopelessness of getting to the standard assumptions for small-mean count data. For the sparse time series in M5, there was nothing to gain and a lot to lose by taking the square root. At the very least, we should have treated those series differently. (Regarding our use of the Kalman Filter, Otto Seiskari’s advice to tune via cross-validation when the model is misspecified is especially compelling).

戴維·沃頓(David Warton)在2018年發表的論文“ 為什么小數位數無法擺脫麻煩 ”，這說明了達到小數位數數據的標準假設的絕望。 對于M5中稀疏的時間序列，通過求平方根沒有任何收益，也有很多損失。 至少，我們應該對這些系列進行不同的處理。 (關于我們對卡爾曼濾波器的使用，當模型指定不正確時， Otto Seiskari的建議通過交叉驗證進行調諧特別引人注目)。

Warton’s paper has some harsh words for users of transformations in general. I still believe that if a transformation brings you closer to the standard assumptions, where your code runs faster and you enjoy nicer properties, then it’s worth considering. But there needs to be an honest exploration of properties of the transformation in the context of the data, and this does not come for free.

一般而言，沃頓的論文對轉??換的使用者來說有些苛刻的話。 我仍然相信，如果 轉換使您更接近標準假設，即代碼運行速度更快并且享受更好的屬性，因此值得考慮。 但是需要在數據的上下文中誠實地探索轉換的屬性，而這并不是免費的。

Typically transformations (and their inverses) are either convex or concave, and thus Jensen’s Inequality will guarantee bias in the form of a Jensen Gap. If you’re wondering why you’ve never heard of it, it’s because it’s often written off as approximation error. According to Gao et al (2018),

通常，變換(及其逆變換)是凸的或凹的，因此Jensen的不等式將保證以Jensen Gap的形式出現偏差。 如果您想知道為什么從未聽說過它，那是因為它經常被記為近似誤差。 根據Gao等人(2018) ，

“Computing a hard-to-compute [expectation of a function] appears in theoretical estimates in a variety of scenarios from statistical mechanics to machine learning theory. A common approach to tackle this problem is to … show that the error, i.e., the Jensen gap, would be small enough for the application.”

從統計力學到機器學習理論，在各種情況下的理論估計中都出現了計算難以計算的[函數期望]。 解決此問題的常用方法是……表明誤差(即詹森間隙)對于應用程序而言足夠小。”

When using transformations, the work to understand the properties of inverse-transformation (in the context of the data) is worth it. It’s dangerous out there. Watch your step, and mind the Jensen Gap!

使用轉換時，了解逆轉換屬性(在數據上下文中)的工作是值得的。 那里很危險。 注意您的腳步，并注意詹森差距！