In the years before 2020, it was common for a large number of school children (20–30 or more) to physically colocate for their math lessons. And in many a class, students were asked to compute the probability that two of them had the same birthday.

在2020年之前的幾年中，大量的學童(20至30歲或更多)為他們的數學課程進行物理布置很普遍。 在許多班級中，要求學生計算他們兩個有相同生日的概率。

To do this computation, students typically make the default assumption that everybody is equally likely to be born on any given day (the uniform distribution). Without this assumption, the problem becomes hard to do by hand. On the other hand, you will often see visualizations floating around the Internet similar to the below.

為了進行此計算，學生通常會默認默認條件，即每個人在任何給定的一天都有相同的可能性出生(均勻分布)。 沒有這個假設，問題就很難手工解決。 另一方面，您經常會看到類似于以下內容的可視化在Internet上浮動。

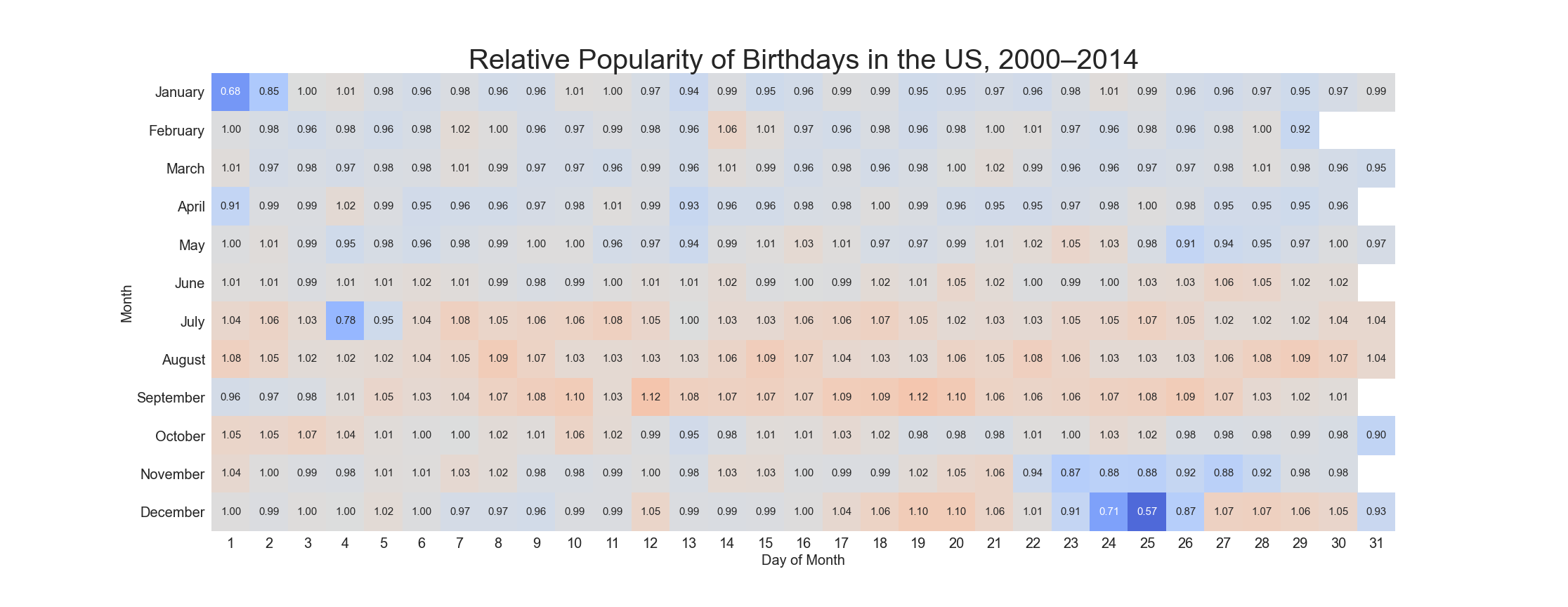
I’ll discuss the data used to generate the figures and values in this article more below. This chart shows the relative likelihood of someone having a birthday on a given day.

我將在下文中進一步討論用于生成圖形和值??的數據。 此圖表顯示某人在給定日期生日的相對可能性。

• A value of 1 (like Dec 16) means that a random person has the same probability of being born on that day as you would expect from a uniform distribution.
  值為1(如12月16日)表示隨機人當天出生的概率與您從均勻分布中預期的概率相同。
• A value lower than one (notably Jan 1, Jul 4, and Dec 24–26) means that a random person is that many times less likely to be born on that day than if the day were chosen uniformly at random.
  小于1的值(尤其是1月1日，7月4日和12月24日至26日)意味著隨機人在那一天出生的可能性比隨機選擇同一天的人少很多倍。
• A value above one (notably mid September) means that a random person is more likely to be born on that day versus what you would na?vely expect.
  大于1的值(特別是9月中旬)意味著與您天真的預期相比，當天隨機的人更有可能出生。

Note that for February 29th, which occurs approximately1 every 4 years, the uniform distribution would imply that one is one-fourth as likely to be born on February 29th as on February 28th. This is accounted for in the chart above (without the correction, a Feb 29 birthday has a relative frequency of 0.92/4 = 0.23 compared to the probability of being born on any other day of the year assuming the uniform distribution).

請注意，對于2月29日(大約每4年發生一次)而言，均勻分布意味著2月29日出生的可能性是2月28日的四分之一。 這在上表中得到了說明(如果不進行更正，則2月29日的生日的相對頻率為0.92 / 4 = 0.23，與假設均勻分布的一年中其他一天的出生概率相比)。

The unpopularity of July 4th, a major holiday in the United States, should tip you off that this data is for the US only.

7月4日(美國主要的假期)的人氣不足，應該提示您該數據僅適用于美國。

In the first part of this article, we will focus on the probability question, namely: what are the odds that two people in a room have the same birthday? First, we will compute the solution to the birthday problem using the assumption that birthdays are uniformly distributed through the year. Second we will use Monte Carlo methods to compute the solution given the observed distribution.

在本文的第一部分中，我們將關注概率問題，即：一個房間中兩個人有相同生日的幾率是多少？ 首先，我們將假設生日在一年中均勻分布，從而計算出生日問題的解決方案。 第二，我們將使用蒙特卡洛方法根據給定的分布來計算解。

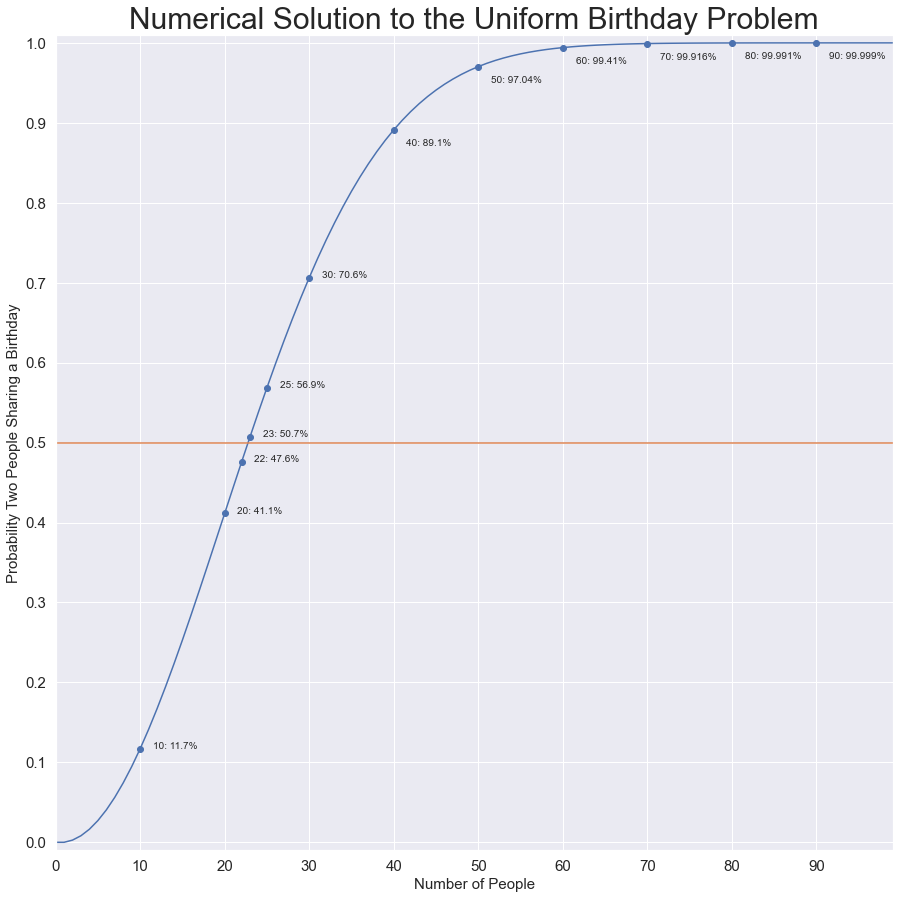
The results will be that the answer is unchanged even considering the empirical distribution (though it gets close!). For each version of the problem we consider, the answer is that 23 is just enough to make the probability of two people having the same birthday 50%.

結果將是，即使考慮經驗分布，答案仍然是不變的(盡管它接近！)。 對于我們考慮的每種問題，答案都是23，足以使兩個人有相同生日的概率為50％。

In the second part of the article, we’ll explore the distribution of birthdays a little bit more and build a simple model to understand the variation in births.

在本文的第二部分，我們將進一步探討生日的分布，并建立一個簡單的模型來了解出生的變化。

統一生日問題 (The Uniform Birthday Problem)

In school, the question could be given as follows:

在學校里，可以提出以下問題：

Suppose there are n people in a room. Assume that nobody has a birthday on February 29th and that their birthdays are random variables uniformly distributed across the other 365 days of the year. Find the minimum value of n such that the probability of at least two students sharing a birthday is at least 50%.

假設一個房間里有n個人。 假設沒有人在2月29日過生日，并且他們的生日是一年中其他365天均勻分布的隨機變量。 求n的最小值，以使至少兩個學生共享生日的概率至少為50％。

To solve this problem, we instead compute the probability that no two students share a birthday. We number the students 1 to n. The probability of the first student not sharing a birthday with any previous student is 365/365=1. For the second student, there are 364 days not overlapping with previous students, so the probability is 364/365 that they don’t share a birthday with a previous student. The next student is 363/365 and so on.

為了解決此問題，我們改為計算沒有兩個學生共享生日的概率。 我們給學生編號1到n 。 第一個學生不與任何以前的學生過生日的概率為365/365 = 1。 對于第二個學生，有364天不與先前的學生重疊，因此他們與先前的學生沒有生日的概率為364/365。 下一個學生是363/365，依此類推。

The result is the following quantity which we will denote q. The goal is to find the minimal n such that q ≤0.5.

結果是以下數量，我們將用q表示。 目的是找到最小的n ，使q≤0.5。

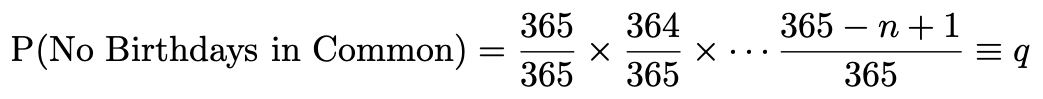
At this point most people reach for their calculator. But we can continue to estimate by hand by taking a logarithm and a Taylor expansion:

在這一點上，大多數人都可以使用他們的計算器。 但是我們可以繼續采用對數和泰勒展開來手動估計：

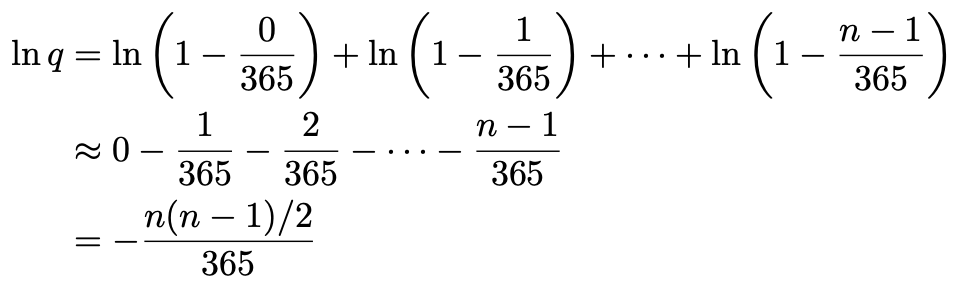
In the first line, we take the logarithm, changing the product into a sum. We also rewrite each fraction in the form of 1–x. The first order Taylor Expansion is a good approximation when x is small, ln(1–x) = –x. This is what we apply in the second line. The third line uses the formulas for the sum of an arithmetic series (we are just adding up 1 + 2 + 3 + ? + (n–1) in the numerator). ln(2) is famously 0.69. Multiplying 0.69?365≈252 (round up). n should be a bit over the square root of 2?252 = 504, so n = 23 is our guess based on these approximations (yielding 253 in the numerator of the ln q approximation). This is in fact the correct answer as the following chart (computed exactly/to numerical precision) shows. Code is linked at the end.

在第一行中，我們采用對數，將乘積更改為總和。 我們還以1-x的形式重寫了每個分數。 當x較小(ln(1–x)= –x)時，一階泰勒展開式是一個很好的近似值。 這就是我們在第二行中應用的內容。 第三行將公式用于算術級數的總和(我們只是將分子中的1 + 2 + 3 +?+(n-1)相加)。 ln(2)是著名的0.69。 乘以0.69?365≈252(向上舍入)。 n應該在2 ^ 252 = 504的平方根上，所以n = 23是我們基于這些近似值的猜測(在ln q近似值的分子中產生253)。 實際上，這是正確的答案，如下圖所示(精確計算/精確到數值精度)。 代碼鏈接在末尾。

經驗生日問題 (The Empirical Birthday Problem)

Now we turn to solving the birthday problem using real data. The data in question is provided by FiveThirtyEight and is based on Social Security Administration (government) data giving birth counts on each day from Jan 1, 2000 to Dec 31, 2014. It’s reasonable to assume this covers nearly every birth in the United States during that time frame.

現在我們轉向使用實際數據解決生日問題。 有問題的數據由FiveThirtyEight提供，并基于社會保障局(政府)數據提供了2000年1月1日至2014年12月31日期間的每一天的出生計數。可以合理地假設此數據涵蓋了在美國期間幾乎所有的出生那個時間范圍。

Taking the data as given, we turn to estimating the probability of two people having the same birthday. We assume the birthdays of our n people are iid distributed according to the empirical distribution of our data. There isn’t a feasible direct way to compute this from the data so, we turn to Monte Carlo methods.

根據給定的數據，我們轉向估計兩個人有相同生日的概率。 我們假設根據數據的經驗分布來分布我們n個人的生日。 沒有一種可行的直接方法可以從數據中計算出來，因此，我們轉向蒙特卡洛方法。

Specifically, for each n, we will sample from the distribution and observe if any birthdays are shared. Again, code (and test cases) are in the repo linked at the end. Somewhat surprisingly, the results are substantively unchanged. The results are graphed below, with the values for the uniform birthday problem plotted as well. The empirical result also has a 99% confidence interval, which is so small you cannot see it (using 100,000 simulations per n).

具體來說，對于每個n ，我們將從分布中采樣并觀察是否共享了任何生日。 同樣，代碼(和測試用例)位于最后的倉庫中。 令人驚訝的是，結果基本上沒有變化。 結果顯示在下面，并繪制了統一生日問題的值。 經驗結果還具有99％的置信區間，這個置信區間是如此之小，您看不到它(每n使用100,000個模擬) 。

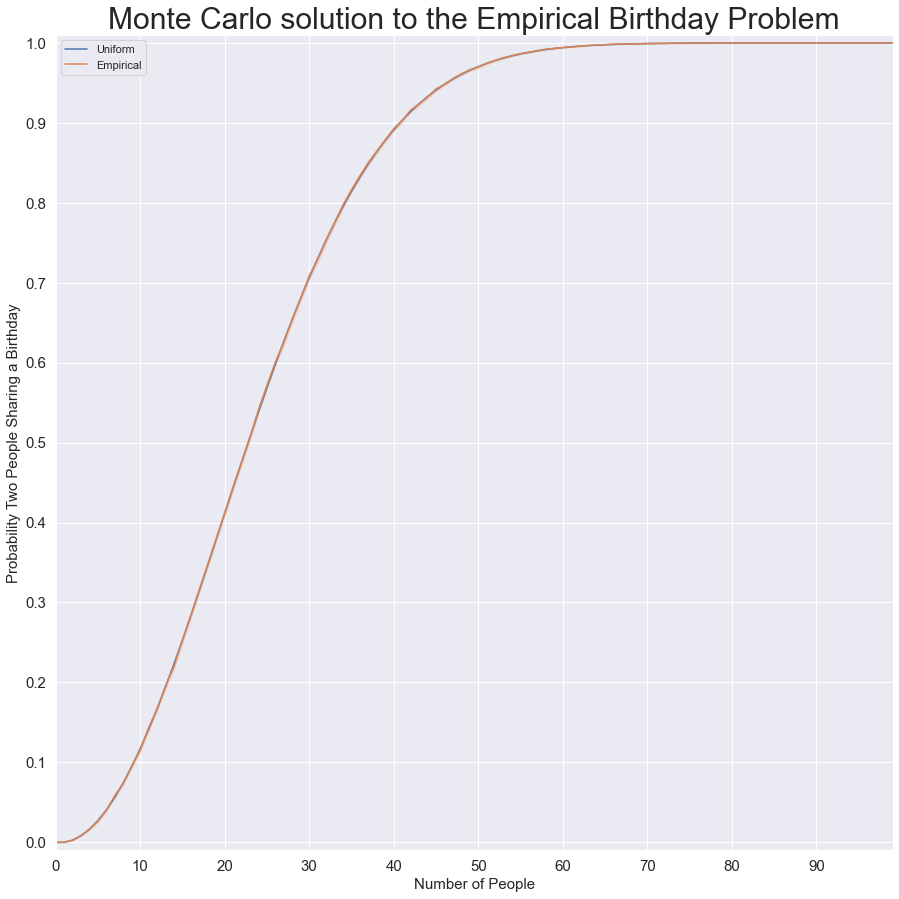
This distribution is close enough to uniform that the result n=23 continues to hold for the empirical case! In a sense, this was, in hindsight, an unnecessary analysis. The difference between the two curves is graphed below, and you can see that they are statistically indistinguishable.

這種分布足夠接近均勻，以至于對于經驗情況，結果n = 23繼續成立！ 從某種意義上說，從事后看，這是不必要的分析。 兩條曲線之間的差異如下圖所示，您可以看到它們在統計上是無法區分的。

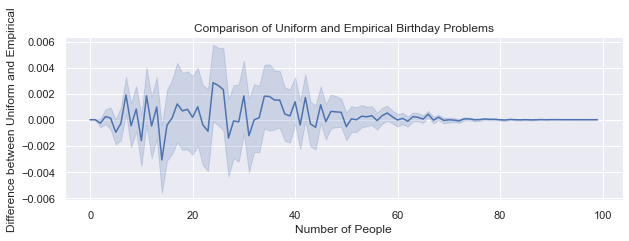
To be clear, the distributions are not the same. However, this simulation was run with 100,000 draws per value of n, not enough statistical power to reveal the differences. Larger numbers of simulations would reveal statistically significant (but substantively small) differences.2 For example, running 5,000,000 draws just for n=23 finally yields enough statistical power to distinguish. The empirical distribution has P=50.786%±0.022%, while the uniform distribution has P=50.730%. (The margin of error is 1 standard deviation, not a 95% confidence interval).

需要明確的是，分布是不相同的。 但是，此模擬使用每個n值100,000次抽獎進行，沒有足夠的統計能力來揭示差異。 大量的仿真將顯示出統計學上顯著的差異(但實質上很小)。2例如，僅在n = 23時運行5,000,000次繪制，最終會產生足夠的統計能力來區分。 經驗分布具有P = 50.786％±0.022％，而均勻分布具有P = 50.730％。 (誤差幅度為1個標準偏差，而不是95％的置信區間)。

一年生日問題 (The Single-Year Birthday Problem)

Now, the deviation of the birth distribution from uniform in any fixed year should be higher than the overall. Much of the variation that we would expect to see in any given year will be smoothed out. For example:

現在，任何固定年份的出生分布與統一的偏差都應該大于整體。 我們希望在任何一年中看到的大部分差異都將被消除。 例如：

• Any given date will cycle through the days of the week over the 14 year period, so the deviation from uniform due to days of the week (discussed below) will be hidden.
  任何給定的日期都將在14年的周期中循環到星期幾，因此將隱藏由于星期幾(下文討論)而導致的統一偏差。
• Thanksgiving (the 4th Thursday in November in the US) is not on the same date every year. Reviewing the table of relative popularities of birthdays, we can see that there is a dip towards the end of November, but it is smoothed out by the slight change in the precise date each year.
  感恩節(美國11月的第4個星期四)不是每年的同一天。 查看生日的相對受歡迎程度表，我們可以看到到11月底有所下降，但每年的確切日期略有變化可以消除這種情況。

Going back to the Birthday problem, this might make us worry. If you ask a typical class of 4th graders in fall 2020, most will be born between September 2010 and August 2011. We would expect higher variability than in the empirical distribution because each of them is much less likely to have been born on a date that, say, happened to be Labor Day in the fall of 2010. This could lead to a different solution (perhaps n=22?) of the Birthday problem.

回到生日問題，這可能使我們擔心。 如果您在2020年秋季要求一個典型的四年級學生，那么大多數人將出生在2010年9月至2011年8月之間。我們期望其可變性高于經驗分布，因為他們每個人的出生日期都不太可能，例如，正好是2010年秋天的勞動節。這可能導致生日問題的另一種解決方案(也許n = 22？)。

To explore this, we can proceed as follows.

為了探索這一點，我們可以進行如下操作。

1. We can quantify the difference. The Kullback–Leibler divergence (KL–div) is a measure of the difference between two probability distributions. For the dataset overall and for each year we can compute the variation of the distribution from uniform.

   我們可以量化差異。 Kullback-Leibler散度 (KL-div)是兩個概率分布之間差異的度量。 對于總體數據集和每年的數據集，我們可以計算出均勻分布的變化。

2. We can re-solve the birthday problem using Monte–Carlo methods and drawing from a distribution based on 1 year. For simplicity, we’ll keep it to a calendar year.
   我們可以使用蒙特卡洛方法并根據1年的分布來重新解決生日問題。 為簡單起見，我們將其保留為日歷年。

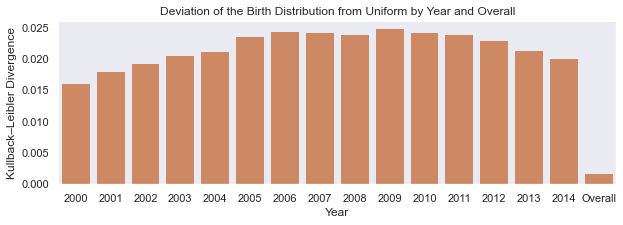
For the first one, we confirm what we expected in the chart below. The divergence from uniform is about 10 times higher on an annual basis (0.021±.006) than on an overall basis (.002). There also appears to be an interesting trend to the data. The only possible explanation I can think of is the gradual cycling of the calendar through the 7 possible start dates of the year. The cycle is messed up by leap years, but roughly speaking we expect, for example, July 4th to move around from Monday to Tuesday to Wednesday etc. on a 6–7 year period.

對于第一個，我們確認下圖中的預期。 每年(0.021±.006)與統一的差異大約是整體(.002)的10倍。 數據似乎也有有趣的趨勢。 我能想到的唯一可能的解釋是日歷從一年的7個可能開始日期開始逐漸循環。 這個周期被leap年弄亂了，但是粗略地說，我們希望例如7月4日在6-7年內從星期一到星期二到星期三等移動。

In terms of re-estimating the birthday problem with annual data, we can do so (using a smaller simulation size of 10000 runs per n). The curves are slightly higher than the uniform distribution (shown in blue). The solution almost changes, but in fact, n=23 still holds up for a room full of people all born in the same year. For n=22, the probability creeps up to as much as 49.1%±.05% for people born in 2009, compared to 47.6% for the uniform distribution.

就用年度數據重新估算生日問題而言，我們可以這樣做(使用每n個10000次運行的較小模擬大小)。 曲線略高于均勻分布(以藍色顯示)。 解決方案幾乎發生了變化，但是實際上，n = 23仍然容納了一個房間，這些房間里都是同一年出生的。 在n = 22的情況下，2009年出生的人的概率上升到49.1％±.05％，而均勻分布的概率為47.6％。

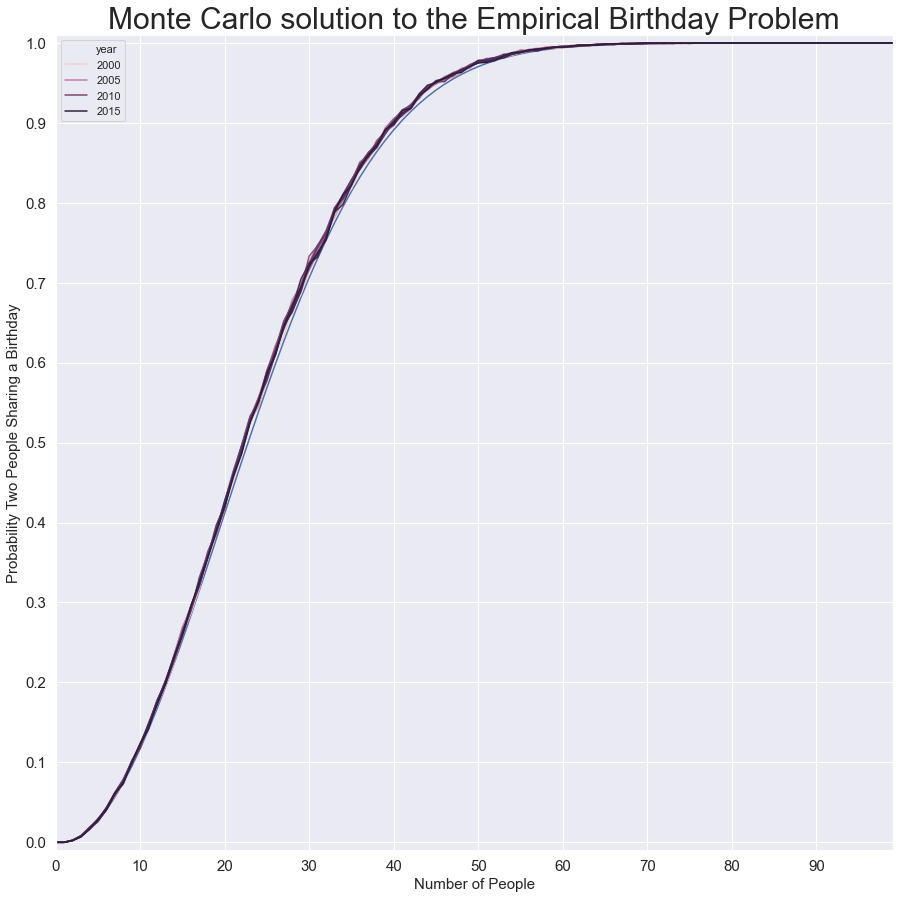
So, it turns out that the uniform assumption is good enough for this problem and there’s no need to fret.

因此，事實證明，統一假設足以解決該問題，因此無需擔心。

生日的分布 (The Distribution of Birthdays)

Since we’re here, let’s see what other insights we can get from the data.

既然我們在這里，讓我們看看我們可以從數據中獲得什么其他見解。

一周中的天 (Day of the Week)

You might be surprised to learn that weekends are not a popular time to give birth. The figure below shows the mean number of births on any given day of the week in our dataset. The 95% confidence intervals are shown and are tight, indicating a statistically significant3 difference between the weekend and weekdays, as well as a noticeably smaller number of births on Mondays.

您可能會驚訝地發現，周末不是生育的熱門時間。 下圖顯示了數據集中一周中任何指定天的平均出生人數。 顯示了95％的置信區間，該區間很小，表明在周末和工作日之間存在統計學上的顯著性差異3，并且星期一的出生人數明顯減少。

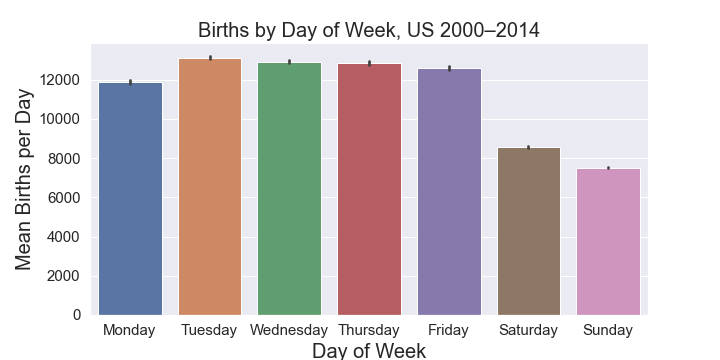
Two hypotheses you might want to keep in mind. Let’s call them the negative and positive hypotheses (for how you might feel about the reasons)

您可能需要牢記兩個假設。 我們稱它們為否定假設和肯定假設(以了解您對原因的看法)

• The negative one, based on previous conversations I’ve had with physicians, is that it’s inconvenient for the obstetricians (the doctors delivering the baby) to have a birth on a weekend. Why be on call all weekend when you can go to your summer house instead? If true, this would be a bit sad because C-sections are expensive to the US healthcare system and they would represent unnecessary surgeries with the attendant risks for the mother.

  根據我之前與醫生的交談得出的負面結論是， 產科醫生 (分娩嬰兒的醫生)在周末出生很不方便。 當您可以去避暑別墅時，為什么整個周末都在待命？ 如果為真，這將使您有些傷心，因為剖腹產對于美國醫療保健系統而言是昂貴的，而且會代表不必要的手術，并給母親帶來隨之而來的風險。

• The positive one, which you can find in this FiveThirtyEight analysis of the data, is that hospitals are fully staffed during the week, so it’s safer and easier to schedule a C-section then.

  您可以從此FiveThirtyEight數據分析中找到積極的一面，那就是醫院在一星期內工作人員配備齊全，因此安排一個剖腹產手術更安全，更容易。

You can read a bit more about this in that FiveThirtyEight article.

您可以在FiveThirtyEight文章中有關此內容。

回歸模型 (Regression Model)

Overall, the general question that you might want to ask about this data is: what explains the variability in births on any given day? Stated this way, we have a classic regression problem. We want to model the data and see what we learn.

總體而言，您可能要問的有關此數據的一般問題是：是什么解釋了給定日期的出生變異性？ 這樣說，我們有一個經典的回歸問題。 我們想對數據建模，看看我們學到了什么。

My goal here is to do a very quick and simple model. For example, we could use sophisticated time-series/forecasting tools like Facebook’s Prophet keep track of a variety of holidays and the run-up to them, each of which could be entered as a regressor. I don’t want to get this fancy, so for covariates we’ll use:

我的目標是建立一個非常快速且簡單的模型。 例如，我們可以使用復雜的時間序列/預測工具，例如Facebook的Prophet來跟蹤各種假期以及假期的運行情況，每個假期都可以作為回歸值輸入。 我不想花哨，所以對于協變量，我們將使用：

1. The month.
   這個月。
2. The year (to account for secular trends/variation in births).
   年(考慮到世俗趨勢/出生變化)。
3. The day of the week.
   星期幾。
4. A handful of holidays non-scientifically chosen by looking at the chart and thinking about major US holidays. The full list is in an appendix below. In total there are 17 holiday covariates.
   通過查看圖表并考慮美國的主要假期，可以非科學地選擇一些假期。 完整列表在下面的附錄中。 總共有17個假期協變量。

Again, a more sophisticated analysis would use geographically disaggregated data and consider a variety of factors like the weather, local sports teams’ performance?, the (local) economy, and just about anything that broadly affects people and makes them and their partner (or surrogates, I guess) decide to get pregnant (or do so accidentally).

同樣，更復雜的分析將使用按地理位置分類的數據，并考慮各種因素，例如天氣，當地運動隊的表現?，(當地)經濟以及幾乎任何會廣泛影響人們并使其與他們的伴侶(或代孕)的因素。 (我想)決定懷孕(或意外懷孕)。

The resulting model is pretty good with an R2 of 94%.? This means that 94% of the variation in births is explained by the model. Here are the coefficients:

結果模型非常好，R2為94％。?這意味著該模型可以解釋94％的出生變異。 以下是系數：

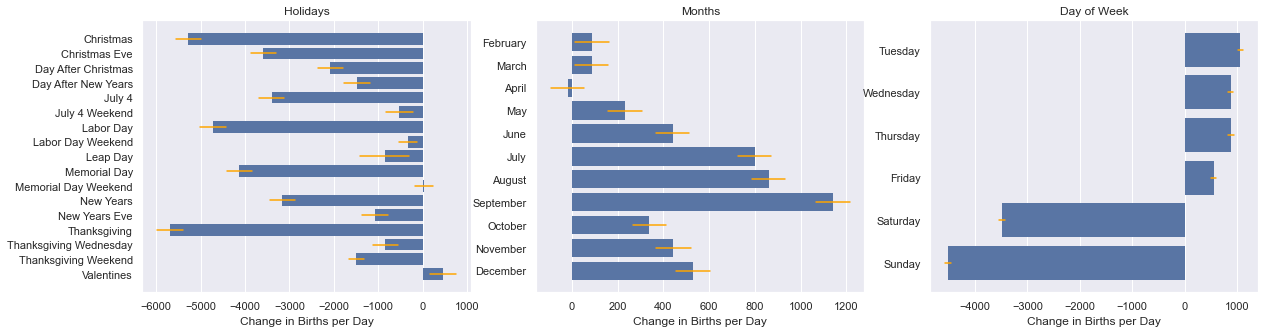
Each coefficient represents the expected change in number of births holding everything else constant. You can find the exact coefficients in the GitHub repo linked at the end. The orange bars show 95% confidence intervals. For example, on Christmas, the coefficient of approximately –5300 means that about 5300 fewer babies are born on Christmas in our dataset than we would otherwise expect after accounting for the month (December), day of the week (varying), and year.

每個系數代表在其他條件不變的情況下出生人數的預期變化。 您可以在最后鏈接的GitHub存儲庫中找到確切的系數。 橙色條顯示95％的置信區間。 例如，在圣誕節，系數約為–5300，這意味著在考慮了月份(12月)，星期幾(不同)和年份之后，我們的數據集中圣誕節出生的嬰兒比我們期望的少了5300個。

For the Months table, the coefficient represents the change relative to January. Thus if we took a day in September versus January in the same year and held everything else constant (day of week, holidays), we would expect to see about 1140 more births on a given day in September. Likewise, for the day of the week, everything is compared to a Monday.

對于“月”表，系數表示相對于一月的變化。 因此，如果我們將9月的一天與同年的1月相比較，并且將其他所有條件保持不變(星期幾，節假日)，那么我們預計9月的某一天將會多出1140胎。 同樣，一周中的每一天，所有內容都將與星期一進行比較。

The intercept (not shown) is the number of births on a regular Monday in January, approximately 12,000 per day. There is also a slight decrease over time, with about 33 fewer births per day for each year after 2000, though further examination (not shown) shows the effect isn’t linear and shouldn’t be over-interpreted.

截距(未顯示)是一月的常規星期一的出生人數，大約每天12,000。 隨著時間的流逝，這種現象也略有減少，2000年以后，每年的出生數每天減少約33，盡管進一步檢查(未顯示)顯示，這種影響不是線性的，不應過度解釋。

Valentines is popular for giving birth, while Memorial day weekend seems just as good as any other weekend. For the remaining holidays, Thanksgiving, Christmas, Labor Day, and Memorial day are quite unpopular. We see substantial but smaller effects for the other days around major holidays.

情人最喜歡生孩子，而陣亡將士紀念日周末似乎和其他任何一個周末一樣好。 在剩下的假期中，感恩節，圣誕節，勞動節和陣亡將士紀念日并不受歡迎。 在重大假期前后的其他幾天，我們看到實質性但較小的影響。

In terms of months, we see a clear trend for births starting in the spring and going into late summer early/fall, peaking in September. Presumably, this represents what parents were choosing to do with their time the previous winter. The day-of-week analysis is substantively similar to what we saw earlier.

就月份而言，我們看到從Spring開始到夏末早期/秋季進入出生的明顯趨勢，在9月達到高峰。 據推測，這代表了父母在上個冬天選擇與自己的時間在一起的事情。 一周中的一天的分析與我們之前看到的基本上類似。

The next question we want to ask is, are there any other days we missed? Displayed below are the residuals of the model, averaged over dates. You should interpret this as the relative popularity of a day after accounting for day of the week, month, and a limited selection of holidays.

我們要問的下一個問題是，我們還有其他日子嗎？ 下面顯示的是模型的殘差，這些殘差是按日期平均的。 您應該將其解釋為考慮了一周中的某天，某月和某天有限的假期后 ，一天的相對受歡迎程度。

Specifically, it shows the mean anomalous number of babies born/not born on each day. These residuals are all rounded to the nearest 10.

具體來說，它顯示了每天出生/未出生的嬰兒的平均異常數。 這些殘差均四舍五入至最接近的10。

A few things jump out immediately. Halloween (October 31) is an unpopular day to give birth that we forgot to include. July 5 is unpopular. In my quick-and-dirty coding of holidays, the Monday after a weekend July 4th (which is often when the day is observed) would not have been included, likely explaining this. December 23rd is also unpopular.

一些事情立即跳出來。 萬圣節(10月31日)是不受歡迎的分娩日，我們忘記了分娩。 7月5日不受歡迎。 在我對假期的快速編碼中，將不包括7月4日周末之后的星期一(通常是一天中的某天)，這可能解釋了這一點。 12月23日也不受歡迎。

The vertical blue stripe on the 13th indicates that, all other things equal, people also don’t like giving birth on the 13th! Nor (since 2001 at least) do they like giving birth on September 11. Looking at the month of December, we see that people prefer to give birth towards the later end of the month: either the week before Christmas or the week between it and New Years.

13號垂直的藍色條紋表示，在所有其他條件相同的情況下，人們也不喜歡13號生育！ 他們也(至少從2001年起)不喜歡在9月11日分娩。從12月份開始，我們看到人們更喜歡在該月下旬分娩：圣誕節前的一周或圣誕節與圣誕節之間的一周。新年。

結論 (Conclusion)

It’s pretty fascinating that people can somehow control when they give birth. It’s hard to say immediately whether it’s a subconscious phenomenon, something about the differing levels of stress, or a deliberate medical intervention, or something else.

人們在出生時可以通過某種方式進行控制，這非常令人著迷。 很難立即說出這是否是一種潛意識現象，是關于壓力水平不同的某種東西，還是故意的醫療干預，還是其他的東西。

We’ve seen that overall, the distribution of births is pretty close to uniform (close enough that the solution to the birthday problem is still n=23). On the other hand, we saw major variation on smaller time scales: in days of the week and when examined on an annual basis. But, even looking on an annual basis, it still wasn’t sufficient to change the solution to the birthday problem.

我們已經看到，總體而言，出生的分布非常接近均勻(足夠接近，生日問題的解決方案仍然是n = 23 )。 另一方面，在較小的時間范圍內，我們看到了很大的差異：在一周中的幾天以及每年進行一次檢查時。 但是，即使按年度來看，仍不足以改變生日問題的解決方案。

Finally, we looked into modeling the variation in births and saw that it is mostly explained by holidays, months, and days of the week. To the remaining unexplained variance, we can point to a few days we forgot to model: the 13th, Halloween, July 4 weekend, Sep 11, and the days around Christmas.

最后，我們研究了出生變化的模型，發現它主要是由假期，月份和一周中的幾天解釋的。 對于其余無法解釋的差異，我們可以指出一些我們忘記建模的日子：13日，萬圣節，7月4日周末，9月11日以及圣誕節前后的日子。

附錄：假期清單 (Appendix: Holiday List)

There are a total of 17 covariates introduced by holidays. For each, if any associated weekend days are included, all weekend days are coded as the same. For example, there is two indicator variable for Labor Day: one for Labor Day itself, and one for Labor Day Weekend.

假期總共引入了17個協變量。 對于每個周末，如果包括任何關聯的周末，則將所有周末編碼為相同。 例如，勞動節有兩個指標變量：一個是勞動節本身，另一個是勞動節周末。

1. New Years, New Years Eve, and the Day After (3)
   元旦，除夕和After日(3)
2. Valentines Day (1)
   情人節(1)
3. Leap Day (1)
   日(1)
4. Memorial Day and the preceding weekend (2)
   陣亡將士紀念日及之前的周末(2)
5. July 4th and any adjacent weekend days, if they exist (2)
   7月4日及以后的任何周末(如果有的話)(2)
6. Labor Day and Labor Day Weekend (2)
   勞動節和勞動節周末(2)
7. Thanksgiving, the day before, and the Fri–Sun following (3)
   感恩節，前一天，以及其后的周五至周日(3)
8. Christmas, Christmas Eve, and the Day After (3)
   圣誕節，平安夜和后天(3)

筆記 (Notes)

[1] It is a sometimes forgotten fact that leap years occur every 4th year unless the year is divisible by 100 but with the caveat that the exception does not apply if the year is divisible by 400. That means that 1900 and 2100 are not leap years, but 2000 is alongside the usual ones: 1996, 2004, 2008 etc. There is no one currently known to be alive that has not experienced a leap year every 4th year during their life (and the data is from 2000–2014), so we can safely treat a leap year as occurring every 4 years for the purpose of our analysis. We will definitely ignore esoteric things like leap seconds which would not substantively affect our analysis.

[1]有時被遺忘的事實是leap年每第4年發生一次， 除非該年可以被100整除， 但是要注意的是，如果年份可以被400整除，則該例外不適用。這意味著1900年和2100年不是leap年年份，但2000年是通常年份：1996年，2004年，2008年等。目前尚無一個活著的人在其生命中每4年經歷過一次a年(且數據來自2000-2014年)，因此，出于分析目的，我們可以安全地將a年視為每4年發生一次。 我們一定會忽略諸如leap秒之類的神秘事物，這些事物不會實質性地影響我們的分析。

[2] I am not going to give a formal proof that a non-uniform distribution should give a different curve. But, intuitively, the uniform distribution minimizes the probability of two people having the same birthday across all distributions supported on the days of the year. Any deviation from this (quantified by the Kullback–Leibler-divergence) must necessarily cause the probability of two people having the same birthday to go up. In the repo, you can find an example where we keep skewing the data more and more and the difference eventually becomes visible to the naked eye.

[2]我不會正式給出不均勻分布應該給出不同曲線的證明。 但是，從直觀上講，在一年中支持的所有分布中，統一分布最大程度地降低了兩個人生日相同的可能性。 對此的任何偏離(由Kullback-Leibler-分歧量化)必然會導致兩個人有相同生日的可能性增加。 在回購中，您可以找到一個示例，在該示例中，我們不斷使數據傾斜，最終差異變得肉眼可見。

[3] Technically we should account for multiple comparisons when assigning p-values. However, it is quite clear that the results will be statistically significant just from looking at the data.

[3]從技術上講，在分配p值時，我們應該考慮多個比較。 但是，很明顯，僅查看數據，結果在統計上就很有意義。

[4] Personally speaking I was born in Minneapolis 252 days after the Minnesota Twins won the world series (the standard gestation time for a human is 280 days).

[4]就我個人而言，我是在明尼蘇達州雙胞胎贏得世界大賽后252天出生于明尼阿波利斯的(人的標準妊娠時間為280天)。

[5] For more data about the goodness of fit, see the Github repo. The RMSE of the fit is about 550 births per day though the distribution has fat tails.

[5]有關適合度的更多數據，請參見Github存儲庫。 盡管分布具有肥大的尾巴，但適合的RMSE每天約550例。