ai 中 統計
Today I plan to cover the following topics: Linear independence, special matrices, and matrix decomposition.
今天,我計劃涵蓋以下主題:線性獨立性,特殊矩陣和矩陣分解。
線性獨立 (Linear independence)
A set of vectors is linearly independent if none of these vectors can be written as a linear combination of other vectors.For example, V1=(1,0) and V2=(0,1). Here, V2 cannot be written in terms of V1. However, V3 (3,4) is linearly dependent as V3 can be expressed as 3V1+4V2.
如果這些向量中的任何一個都不能寫成其他向量的線性組合,則它們是線性獨立的,例如V1 =(1,0)和V2 =(0,1)。 在此,不能用V1來寫V2。 但是,V3(3,4)與線性相關,因為V3可以表示為3V1 + 4V2。
Mathematically, s={V1, V2,…., Vn} is linearly independent if and only if the linear combination α1V1+α2V2+…..+αnVn=0 means that all αi=0.
在數學上,當且僅當線性組合α1V1+α2V2+ .... +αnVn= 0表示所有αi= 0時,s = {V1,V2,....,Vn}是線性獨立的。
矩陣運算 (Matrix operations)
Matrices can transform one vector to another vector. For example, V is an Nx1 vector and w is also an Nx1 vector.
矩陣可以將一個向量轉換為另一向量。 例如,V是Nx1向量,w也是Nx1向量。
矩陣的痕跡 (Trace of a matrix)
Trace of a matrix is given by its sum of diagonal elements. For matrix A, its trace will be the summation of all the elements with the same value of row and column.
矩陣的跡線由對角元素的總和給出。 對于矩陣A,其軌跡將是具有相同行和列值的所有元素的總和。
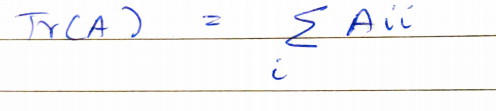
一些屬性 (Some properties)
- Tr(A+B) = Tr(A)+Tr(B) Tr(A + B)= Tr(A)+ Tr(B)
- Tr(AB) = Tr(BA) Tr(AB)= Tr(BA)
- Tr(A) = Tr(A.T) (A.T means transpose of matrix A) Tr(A)= Tr(AT)(AT表示矩陣A的轉置)
矩陣的行列式 (The determinant of a matrix)
Laplace expansion for an NxN matrix is given by the following formula:
NxN矩陣的拉普拉斯展開式由以下公式給出:

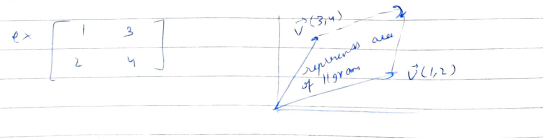
Determinant actually represents the volume formed by the column vectors. For a 2x2 vector, it represents the area.
行列式實際上表示由列向量形成的體積。 對于2x2向量,它表示面積。
矩陣的可逆性 (Invertibility of a matrix)
The inverse of a matrix A is possible only if the det(A) is not 0. Note that this automatically means that the columns of A have to be linearly independent. Consider a matrix below.
僅當det(A)不為0時,矩陣A的逆才可能。請注意,這自動意味著A的列必須線性獨立。 考慮下面的矩陣。
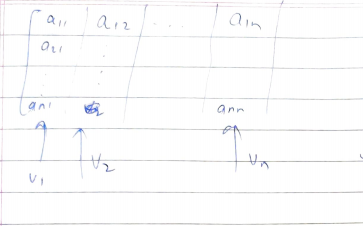
Note that V1, V2,…., Vn are vectors and if any vector, say, Vn can be written as linearly dependent vectors of the rest like Vn=α1V1+α2V2+…..+αn-1Vn-1 then, we can do a simple column operation i.e last column = the last column- (α1V1+α2V2+…..+αn-1Vn-1) and this would yield a column full of zeros. This will make the determinant of matrix 0. For a 2x2 matrix, we will have 2 vectors V1 and V2. If V1 and V2 are linearly dependent like V1=2V2, then the area formed by the two vectors is going to be zero. A smart way to put this would be that the two vectors are parallel to one another.
請注意,V1,V2,...,Vn是向量,如果有任何向量,例如,Vn可以寫為其余部分的線性相關向量,例如Vn =α1V1+α2V2+ ..... +αn-1Vn-1,那么我們可以一個簡單的列運算,即最后一列=最后一列-(α1V1+α2V2+ ..... +αn-1Vn-1),這將產生一列充滿零的列。 這將決定矩陣0的行列式。對于2x2矩陣,我們將有2個向量V1和V2。 如果V1和V2是線性相關的,例如V1 = 2V2,則由兩個向量形成的面積將為零。 一種明智的解釋是,兩個向量彼此平行。
特殊矩陣和向量 (Special matrices and vectors)
- Diagonal matrix: Only diagonal entries are non zero and rest all elements are zero. D(i,j) = 0 if i is not equal to j. 對角矩陣:僅對角線條目為非零,其余所有元素為零。 如果i不等于j,則D(i,j)= 0。
- Symmetric matrix: A matrix is said to be symmetric if the matrix and its transpose are equal. 對稱矩陣:如果矩陣及其轉置相等,則稱該矩陣是對稱的。
- Unit vector: vector with unit length. 2-Norm of the vector is 1. 單位向量:單位長度的向量。 向量的2范數為1。
- Orthogonal vectors: Two vectors X and Y are orthogonal if (X.T)Y = 0 正交向量:如果(XT)Y = 0,則兩個向量X和Y是正交的
- Orthogonal matrix: If a transpose of a matrix is equal o its inverse, then we can say that the matrix is orthogonal. Also, all columns are orthonormal. The orthogonal matrix can be used to rotate vectors which preserve volume. 正交矩陣:如果矩陣的轉置等于其逆,則可以說矩陣是正交的。 同樣,所有列都是正交的。 正交矩陣可用于旋轉保留體積的向量。
- Orthonormal matrix: If the inverse of a matrix is equal to its transpose with unit determinant, the matrix is said to be orthonormal. 正交矩陣:如果矩陣的逆等于其行列式的轉置,則稱該矩陣為正交的。


本征分解 (Eigen decomposition)
Eigen decomposition is extremely useful for a square symmetric matrix. Let's look at the physical meaning of the term.
本征分解對于平方對稱矩陣非常有用。 讓我們看一下該術語的物理含義。
Every real matrix can be thought of as a combination of rotation and stretching.
每個實數矩陣都可以視為旋轉和拉伸的組合。

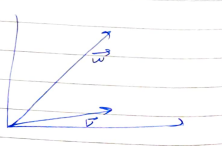
Here, A can be thought of as an operator tat stretches and rotates a vector v to obtain a new vector w. Eigenvectors for a matrix are those special vectors that only stretch under the action of a matrix. Eigenvalues are the factor by which the eigenvectors stretch. In the equation below, the vector v is stretched by a value of lambda when operated with an eigenvector A.
在這里,可以將A視為操作員tat拉伸并旋轉向量v以獲得新的向量w。 矩陣的特征向量是那些僅在矩陣作用下才拉伸的特殊向量。 特征值是特征向量伸展的因子。 在下面的公式中,向量v在使用特征向量A時被拉伸了一個lambda值。
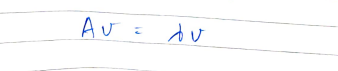
Say, A has n linearly independent eigenvectors {V1, V2,….., Vn}. On concatenating all the vectors as a column, we get a single eigenvector matric V where V=[V1, V2,….., Vn]. If we concatenate the corresponding eigenvalues into a diagonal matrix i.e Λ=diag(λ1, λ2,…, λn), we get the eigendecomposition (factorization) of A as:
假設A有n個線性獨立的特征向量{V1,V2,…..,Vn}。 將所有向量連接為一列后,我們得到單個特征向量矩陣V,其中V = [V1,V2,.....,Vn]。 如果將對應的特征值連接到對角矩陣即Λ = diag(λ1,λ2,...,λn),則得到A的特征分解(因式分解)為:
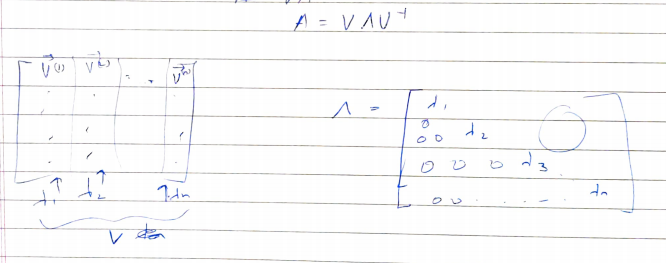
Real symmetric matrices have real eigenvectors and real eigenvalues.
實對稱矩陣具有實特征向量和實特征值。
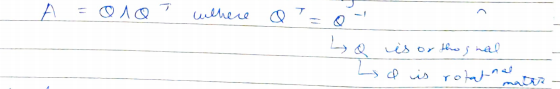
二次形式和正定矩陣 (Quadratic form and positive definite matrix)
The quadratic form can be interpreted as a ‘weighted’ length.
二次形式可以解釋為“加權”長度。
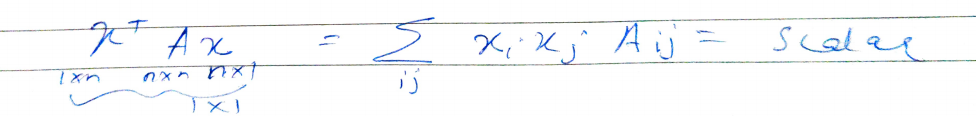

The positive definite (PD) matrix has all eigenvalues greater than zero. The semi-definite positive(PSD) matrix has eigenvalues greater than equal to zero. A PD matrix has a property that for all X, (X.T)AX is greater than 0. For example, if A=I or identity matrix then, (X.T)I(X)=(X.T)(X) which is greater than 0. A PSD matrix has a property that for all X, (X.T)AX is greater than equal to 0. Similarly, a negative definite (ND)matrix has all eigenvalues less than zero. And semi-negative definite (PD)matrix has all eigenvalues less than equal to zero.
正定(PD)矩陣的所有特征值均大于零。 半定正(PSD)矩陣的特征值大于零。 PD矩陣的屬性是,對于所有X,(XT)AX都大于0。例如,如果A = I或單位矩陣,則(XT)I(X)=(XT)(X)大于0. PSD矩陣具有以下特性:對于所有X,(XT)AX都等于0。類似地,負定(ND)矩陣的所有特征值均小于零。 半負定(PD)矩陣的所有特征值均小于零。
奇異值分解 (Singular value decomposition)
If A is an MxN matrix, then
如果A是MxN矩陣,則
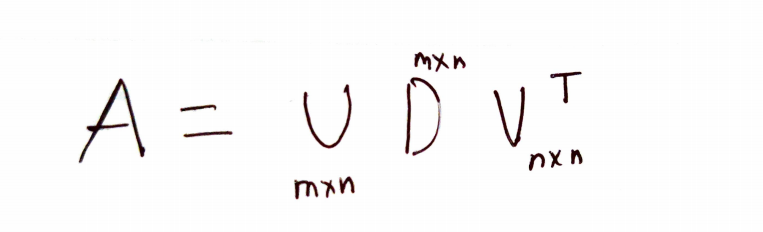
- U is an MxM matrix and orthogonal U是MxM矩陣并且正交
- V is an NxN matrix and orthogonal V是NxN矩陣并且正交
- D is an MxN matrix and diagonal D是MxN矩陣和對角線
- Elements of U are the eigenvectors of A(A.T), called left singular vectors U的元素是A(AT)的特征向量,稱為左奇異向量
- Elements of Vare the eigenvectors of (A.T)A, called right singular vectors Vare的元素(AT)A的特征向量,稱為右奇異向量
- Non zero elements of D are the square-root( λ((A.T)(A))) which means square-root of eigenvalues of (A.T)(A), called as singular values D的非零元素是平方根(λ((AT)(A))),它表示(AT)(A)特征值的平方根,稱為奇異值
結束 (End)
Thank you and stay tuned for more blogs on AI.
謝謝,請繼續關注更多有關AI的博客。
翻譯自: https://towardsdatascience.com/statistics-for-ai-part-2-43d81986c87c
ai 中 統計
本文來自互聯網用戶投稿,該文觀點僅代表作者本人,不代表本站立場。本站僅提供信息存儲空間服務,不擁有所有權,不承擔相關法律責任。 如若轉載,請注明出處:http://www.pswp.cn/news/388300.shtml 繁體地址,請注明出處:http://hk.pswp.cn/news/388300.shtml 英文地址,請注明出處:http://en.pswp.cn/news/388300.shtml
如若內容造成侵權/違法違規/事實不符,請聯系多彩編程網進行投訴反饋email:809451989@qq.com,一經查實,立即刪除!



)








)




)
