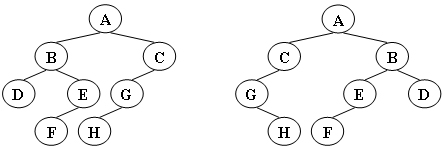
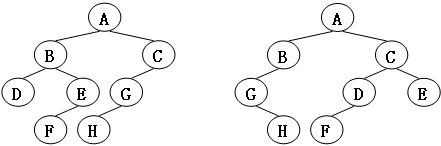
給定兩棵樹T1和T2。如果T1可以通過若干次左右孩子互換就變成T2,則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的,因為我們把其中一棵樹的結點A、B、G的左右孩子互換后,就得到另外一棵樹。而圖2就不是同構的。
?
?
圖1
圖2
現給定兩棵樹,請你判斷它們是否是同構的。
?
輸入格式:
輸入給出2棵二叉樹樹的信息。對于每棵樹,首先在一行中給出一個非負整數N?(≤),即該樹的結點數(此時假設結點從0到N?1編號);隨后N行,第i行對應編號第i個結點,給出該結點中存儲的1個英文大寫字母、其左孩子結點的編號、右孩子結點的編號。如果孩子結點為空,則在相應位置上給出“-”。給出的數據間用一個空格分隔。注意:題目保證每個結點中存儲的字母是不同的。
輸出格式:
如果兩棵樹是同構的,輸出“Yes”,否則輸出“No”。
輸入樣例1(對應圖1):
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
輸出樣例1:
Yes
輸入樣例2(對應圖2):
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
輸出樣例2:
No//error #include<cstdio> const int maxn = 11; int n; int *solve(){scanf("%d",&n);int count[maxn]={0};for(int i = 0; i < n; i++) printf("%d ",count[i]);char a,b,c;for(int i = 0; i < n; i++){scanf("%*c");scanf("%c %c %c",&a,&b,&c);int add = 2;if(b == '-') add--;if(c == '-') add--;count[a -'A']+=add; }printf("%d",count[3]);return count; }int main(){int* a = solve();int* b = solve();for(int i = 0; i < n; i++){printf("%d %d\n",a[i],b[i]);} // if(n==1){ // printf("no\n"); // return 0; // } // int i; // for(i = 0; i < n; i++){ // if(a[i] != b[i]){ // printf("No\n"); // break; // } // } // if(i == n)printf("Yes\n");return 0; }
//correct #include<cstdio> const int maxn = 11; int countsa[maxn]; int countsb[maxn];int main(){int n;scanf("%d",&n);for(int i = 0; i < n; i++){int add = 2;char a,b,c;scanf("%*c");scanf("%c %c %c",&a,&b,&c);if(b == '-') add--;if(c == '-') add--;countsa[a-'A']+=add;}scanf("%d",&n);for(int i = 0; i < n; i++){int add = 2;char a,b,c;scanf("%*c");scanf("%c %c %c",&a,&b,&c);if(b == '-') add--;if(c == '-') add--;countsb[a-'A']+=add;}if(n==1){ printf("No\n"); return 0; } int i; for(i = 0; i < n; i++){ if(countsa[i] != countsb[i]){ printf("No\n"); break; } } if(i == n)printf("Yes\n");return 0; }
?


)


)

)


)
目錄)
)
)

)

)
 (25 分))
