直接排序

直接使用Java已有的方法進行排序，這一招…大意了！

這題簡單，就是個基本的排序，后面難題，可能這只是一小步，內個時候直接用排序算法比較合適，這個不合適。。

class Solution {public void merge(int[] A, int m, int[] B, int n) {for(int i = 0; i < n; i++){A[m+i] = B[i];}Arrays.sort(A);}
}

我們看看方法

這是一個更優的快速排序算法，對于某些數據，傳統的快速排序可能會退化為二次方的事件復雜度，而此算法會更快一些，是O(n log(n))。

這種方式，頂多算應用黑箱子，沒啥可以說的…

雙指針 + 臨時數組

我們可以對每個數組都添加一個索引指針，依次對比兩個數組的值，讓最小的進入臨時數組，比較之后，把剩余的數直接放入臨時數組，最后，臨時數組再賦值給A。

leetcode的動圖很好，直接放出來鏈接。

雙指針

class Solution {public void merge(int[] A, int m, int[] B, int n) {int[] temp = new int[m+n];int i = 0; // array A pointerint j = 0; // array B pointerint k = 0; // array temp pointerwhile(i < m && j < n){if(A[i] < B[j]){temp[k++] = A[i++];} else if(A[i] >= B[j]){temp[k++] = B[j++];} }// 剩余部分while(i < m){temp[k++] = A[i++];}while(j < n){temp[k++] = B[j++];}k = 0;i = 0;while(k < m + n){A[i++] = temp[k++];}}
}

這種方法，實現起來很簡單，其實就是依次比較，但是開辟新的數組，再放回去，就很麻煩。

同樣的思路，不同的實現方式

對于同樣的邏輯，代碼寫起來其實也不一定一樣的！我們看一看！

逆向雙指針

所以，我們嘗試一下在數組A直接動手腳，利用數組A中后半部分的剩余空間，看看可不可行！

關鍵點：A中的元素會不會被覆蓋

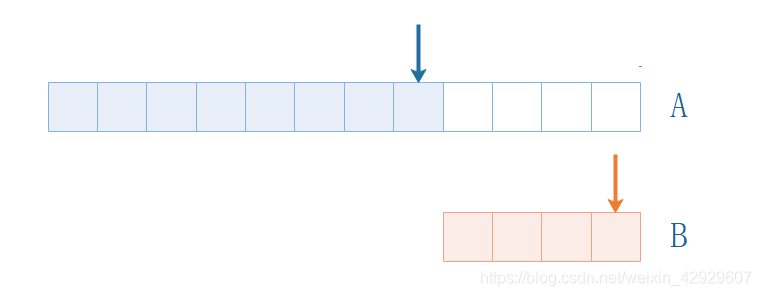
我們可以，從兩數組的后面開始，比較誰大，將大的放進A的最后面。

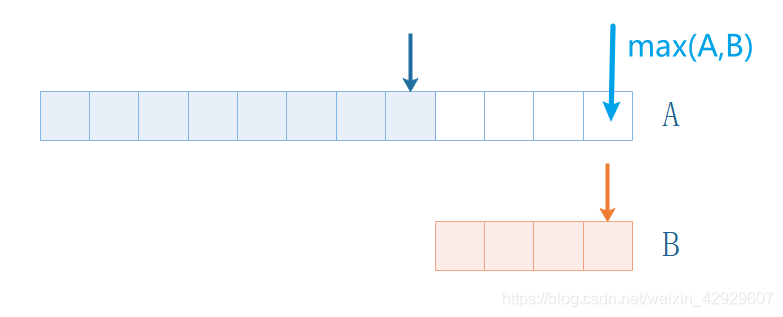
這里，我們列舉極端例子

1. B中的元素，全部比A中最大的還大

那么，Ｂ中的元素全部放入A的剩余空間中去，顯然，沒有問題！

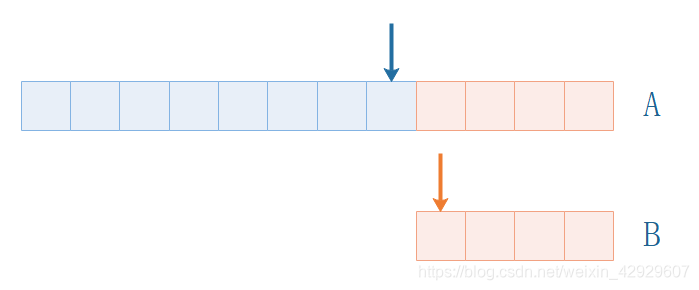
2. B的元素，比A的元素都小

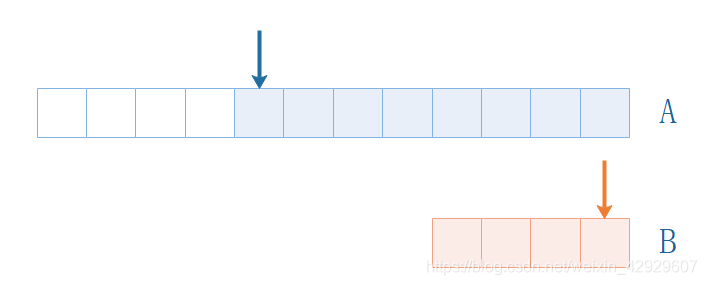
當然也能放進去。

最后，我們看看中間狀態，也就是正常狀態

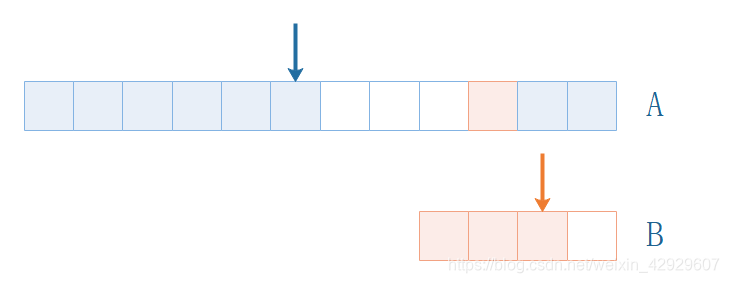
很容易分析得出，不管怎么樣，A中的剩余空間一定夠用！

因此寫代碼實現：

class Solution {// 逆向雙指針public void merge(int[] A, int m, int[] B, int n) {int ap = m - 1;int bp = n - 1;int final_pointer = m + n - 1;while(ap >= 0 && bp >= 0){if(A[ap] > B[bp]){A[final_pointer--] = A[ap--];} else{A[final_pointer--] = B[bp--];}}// 若A剩余，就不用管了；若B剩余，都扔進去while(bp >= 0){A[final_pointer--] = B[bp--];}}
}

或者可以

class Solution {// 逆向雙指針public void merge(int[] A, int m, int[] B, int n) {int ap = m - 1;int bp = n - 1;int final_pointer = m + n - 1;while(bp >= 0){// 置換A的元素if(ap >= 0 && A[ap] > B[bp]){   // 注意順序不要寫反！A[final_pointer--] = A[ap--];} else {// 置換B的元素A[final_pointer--] = B[bp--];}}}
}

后者寫法簡潔一些，前者寫法更加明了，是繼承解法二的思想。

我們用嚴格的方式再說明一下A不會被覆蓋的問題。

我們只需要滿足

• A中可用的位置 >= （A已經置換的數量 + B已經置換的數量）

因此，我們分別表示一下

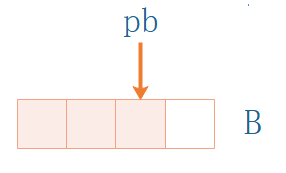
我們要求的是白格子的數量，是

• n - (pb + 1) = n - pb - 1
• pb是索引，從0開始，因此，橙色一共pb + 1個，總數是n，減一下就行了

A同理

• m - pa - 1

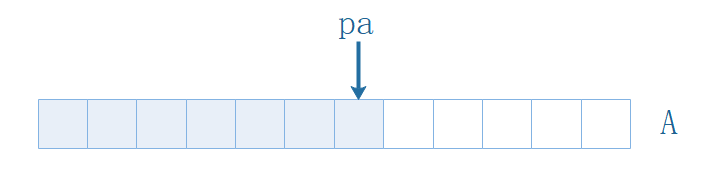
當前數組A可插入數量應該是m + n - pa - 1。

我們求的這三個數分別是（在同一時刻）

• f1:A扔到A后面去的
• f2:B扔到A后面去的
• f3:A后面總共可以插入的元素（不被覆蓋的情況下）

我們只需要驗證f3 >= f1 + f2恒成立即可！

=> pa >= -1顯然恒成立。