針對能夠影響OF和CF標志位的指令，一般來說是涉及到數據運算的指令，這里使用add舉例，即不區分有無符號的加法指令，參與運算的數據，從二進制層級去考慮。

CF標志位

對于CF，它是carry flag，進位標志，這個進位，表示的是二進制層次下的進位，例如：

mov al,98h
add al,al

它的運算是

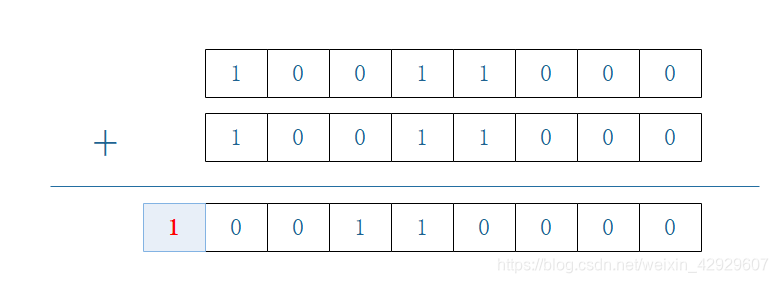
其中，得到的最高一位，會被丟棄，這個也就是進位了！

模擬一下：

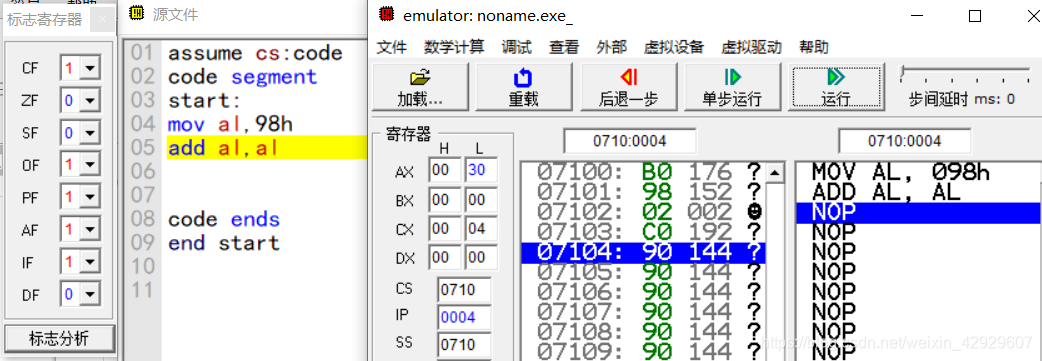
這個進位還是很簡單的！

如何實現add指令進位時，CF的變化

這個簡單，我們只需要記錄一下add的結果的假想最高位即可，就是加法器的進位位。

功能層級理解CF & 進位借位

其實我們只需要從功能角度去理解就可以了，不用關注具體如何實現的，因為這可能非常復雜，不過你的確可以簡單思考一下。

CF不僅僅記錄add時候的進位，也記錄sub時候的借位，同時如何想使用這個進位或者借位，還有sbb，add等指令。

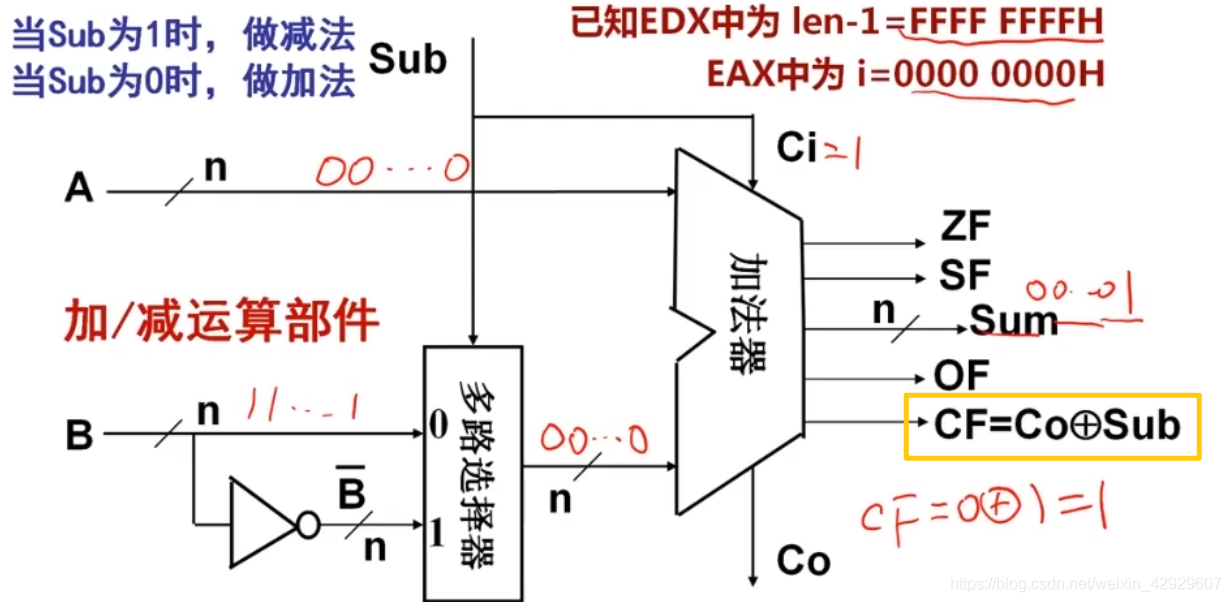
考慮借位的時候，只需要CF的結果等于加法器進位異或sub即可。

OF標志位

overflow flag，溢出標志位，它記錄的不是二進制下的進位，而是十進制下的不合理結果，例如

• 正數 + 正數 = 負數
• 負數 + 負數 = 正數
• ……

我們舉個例子，分別從二進制和十進制下看待這個問題。

mov al,98
add al,99

• 從十進制角度，98 + 99 = 197，但是對于8位補碼，數據范圍是-128 - 127，197是不合理的，它溢出了，因此OF 置 1。
• 從二進制角度，98 + 99 = 62h + 63h = c5h，我們可以看到，單從計算機世界來說,兩數相加，結果并沒有進位，因此CF = 0

我們可以看到，從二進制世界來說，可以很容易識別出進位，但是不容易識別出溢出，因為溢出的規則，是由人類世界的十進制法則決定的，要想實現識別，應該單獨設定一些其他邏輯。

因此，我們要聯合人類世界和計算機世界，來思考如何實現OF標志位的邏輯。

OF標志置位復位的實現

我們先考慮一下可能溢出的場景（8位二進制補碼真值范圍 -128 ~ 127）

• 負數 + 負數 = 正數
• 正數 + 正數 = 負數
• 其他…

我們就先假定至于這兩種場景吧，那么如何實現OF的邏輯？很簡單，列真值表！

我們規定輸入

• 操作數1為正數記為0，負數記為1（其實就是最高位）
• 運算：加法為0，減法為1
• 操作數2為正數記為0，負數記為1
• 運算結果為正數記為0，負數記為1

輸出OF

操作數1	操作	操作數2	運算結果	OF
1	0	1	0	1
0	0	0	1	1
…	…	…	…	0
…	…	…	…	1

這樣我們就能夠根據真值表，得到一個組合邏輯，實現OF了。

當然這只是一個思路而已，舉這個例子是為了說明，OF的實現是與十進制運算密切相關的，僅依靠二進制看不出來。

CF與OF分開看

我們前面可以知道，CF有CF的實現邏輯，OF有OF的實現邏輯，實際執行add運算的時候，我們根據

• 操作數1
• add運算
• 操作數2
• 運算結果

這幾個因素，來分別生成OF和CF的結果，二者在機器層級上是相互獨立并行工作的兩個組合邏輯。

也就是說，CF與OF的組合可能是

• 00
• 01
• 10
• 11

并且二者沒有什么關聯。

CF、OF與有無符號（整）數運算的關系

注意暫時不談浮點數！

首先，有無符號是從高級語言層級才能看出來，add指令進行加法運算，不區分有無符號，不管高級語言是有符號加還是無符號加，都是add指令，結果完全一樣，因此，僅憑借add指令是無法區分的。

那如何區分呢？依靠其他指令以及CF、OF標志位！

通常來說

• CF用于識別無符號數運算的溢出，因為無符號數運算溢出，等價于二進制運算進位了。
• OF用于識別帶符號數運算的溢出，這個邏輯的設置，本身就針對帶符號數，沒什么好說的，補碼就針對帶符號數

這里再強調人類世界與計算機世界關于整數的轉換規則

• 帶符號數：補碼
• 無符號數：二進制位串

運算與標志位的關系

• 無含義的純結果：對于sub,add這種不區分有無符號運算的指令，標志位的結果只和運算結果有關，也不需要分開看。

• 根據其他指令識別標志位，給結果賦予含義：但是如果我們去利用標志位做識別，就需要進行分開看，不同的標志位識別，決定了這個運算結果的不同含義，決定了它是帶符號數還是無符號數運算，亦或者是比較運算。