學習樹狀數組已經兩周了，之前偷懶一直沒有寫，趕緊補上防止自己忘記（雖然好像已經忘得差不多了）。
作為一種經常處理區間問題的數據結構，它和線段樹、分塊一樣，核心就是將區間分成許多個小區間然后通過對大區間的調用來提升效率。因此，我們主要需要了解的就是這種分塊方式。
不同于線段樹直接將區間不斷的進行二分，我們將區間二分的同時將父節點直接放在右區間上，從而形成了一個占用空間很小的樹。
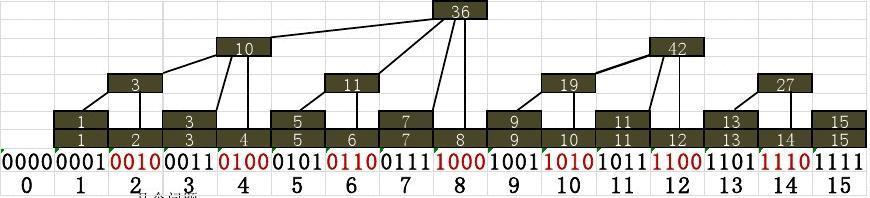
我們仔細觀察這張圖：根據我們剛才的思想，每個右節點都儲存著左右兩個子區間的和，即右節點本身就是自己的父節點，而右節點的父節點就是父節點的父節點。想象一下，原本是一個立體的二叉樹，我們現在將它向右壓，硬生生將一個二維的樹壓成了一個數組，就得到——樹狀數組！！！
雖然占用空間大大減小，但是對結點的訪問現在變成了一個問題，我們應該怎么訪問父親結點和子節點呢？
仔細觀察，我們發現結點n是x個結點的祖先，這個x就是n的二進制的不為零的最小位（不要問我為什么能看出來，我也看不出來啊，也不知道哪位神仙想出來的），我們用一個函數lowbit(n)來表示這個神奇的數字。因為父節點是右偏的（杜撰的專業術語233），所以右邊lowbit(n)個元素和這個區間是并列的，并且右邊lowbit(n)長的區間最右邊的元素是左右兩個區間的祖先，它的位置我們很容易得到是n+lowbit(n)——這就是子節點到父節點的訪問方式。
結點n是左邊lowbit(n)個元素的祖先，所以n-lowbit(n)就是另外一個與n所在區間緊鄰而且沒有重疊的區間，所以我們想要遍歷n以前所有的元素時只需要不斷的進行n-lowbit(n)直到n==0表示已經跳出區間，通過這種方法我們能夠方便的得到前綴和。
通過上面的總結，我們得到了對樹狀數組進行訪問的初步方法。
lowbit()函數的實現方式一般開來說時lowbit(x)=x&(-x);至于為什么這就涉及到玄學的二進制知識，有興趣的話自己去了解一下吧。
根據以上分析，我們可以得到初步的對樹狀數組建立以及維護的方法：
假如我們想要得到的是區間求和：
int lowbit(x)
{return x&(-x);
}
void update(int x,int y)
{for(;x<=n;x+=lowbit(x)) //x+lowbit(x)是包含x元素的父節點 {c[x]+=y;}
}
如何進行查詢呢？
int sum(int x) //x的前綴和
{int ans=0;for(;x;x-=lowbit(x)){ans+=c[x];}return ans;
}
如果想要得到中間一段區間的和，不難想到query(x,y)=sum(y)-sum(x-1);
這樣，我們就初步實現了樹狀數組的維護和查詢。
下附一道練手題：
POJ - 2352 Stars
大概意思就是說求一個二維數組中處于左下角的元素的個數。乍一看好像是一個二維的樹狀數組，但是分析一下數據范圍就會發現不太現實。而且題目中說給出的數據是有順序的，因此我們可以分析一下，不難發現（就當作不難吧）后面輸入的數據對前面輸入的數據是沒有影響的，而且對于每一顆星星來講，處于它下方右邊的并沒有什么意義，因此我們不妨將這個圖形一維化，每個星星的亮度就是所有處于它左邊（和它所在位置但不包括它）星星的個數。問題的思路應該很清晰，下附ac代碼：
#include<cstdio>
#include<cstring>
using namespace std;const int maxn=32005;
int n;
int c[maxn];
int ans[maxn];int lowbit(int x)
{return x&(-x);
}
void update(int x)
{for(;x<=maxn;x+=lowbit(x)){c[x]++;}
}
int sum(int x)
{int ans=0;for(;x;x-=lowbit(x)){ans+=c[x];}return ans;
}
int main()
{int u,v;memset(c,0,sizeof(c));memset(ans,0,sizeof(ans));scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d%d",&u,&v);u++;//需要注意樹狀數組的下標必須從1開始！！！ans[sum(u)]++;update(u);}for(int i=0;i<n;i++){printf("%d\n",ans[i]);}return 0;
}
至于樹狀數組的區間修改區間查詢，將會在樹狀數組的進一步理解中說明。
)
)
