時隔多年我終于又開始寫博客了，主要是已經放假了，之前一直忙于考試和課設沒有時間寫博客，學習筆記也因為買了iPad的緣故大部分都是手寫的了。

假期想要把以前做過的項目都整理一下放在github和CSDN上。

也已經很久沒有寫算法題了，直接導致今天這道題雖然我看了題解但是自己還是寫了好久。

題目描述

傳送門

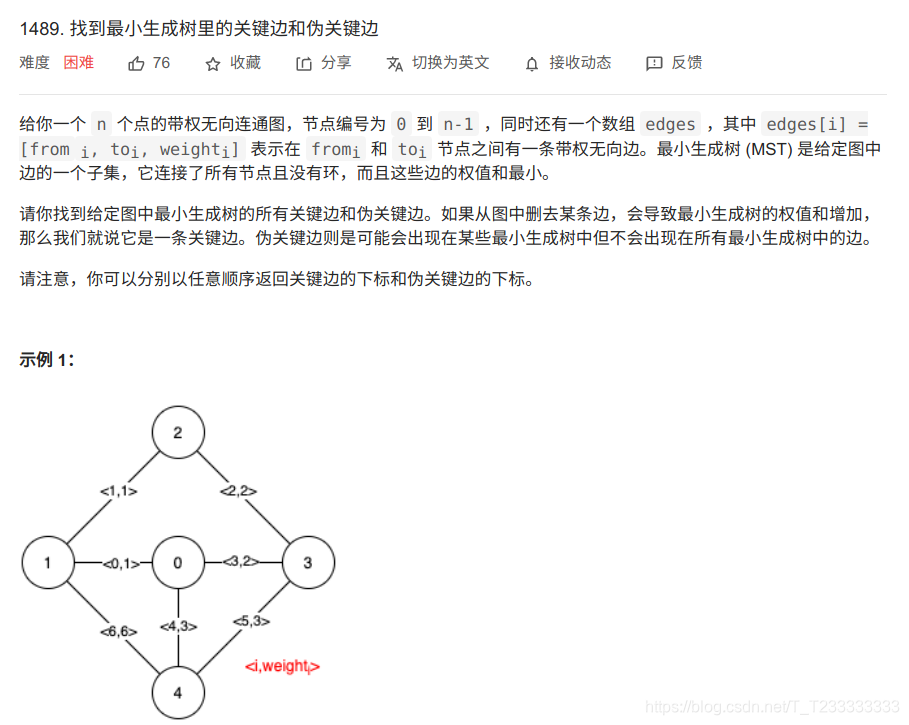
題目解析

題解有兩種解法
第一種解法比較樸素，就是按照關鍵邊和偽關鍵邊的定義。
關鍵邊：在所有MST中都會出現的邊
關鍵邊性質：刪除以后只能得到一個邊權和更大的MST（或者無法得到MST）
偽關鍵邊：會出現在一些MST中但是不會出現在所有MST中的邊

因此，我們對每條邊先判斷是不是關鍵邊，如果不是再判斷是否是偽關鍵邊。
判斷關鍵邊的思路很清晰，就是刪去這條邊再判斷是否還能得到和之前邊權和相同的MST。

但是判斷偽關鍵邊就有一些技巧了：我們很難得到所有的最小生成樹，對于一條邊我們如何判斷這條邊在不在MST中呢，題解的做法是最先將這條邊加入到MST中，然后再對剩下的求解MST，如果最后MST和之前的權值和相同則說明這條邊在MST中。

我和題解不同的做法在于（我認為是一點小優化）：

• 剛開始需要求一次MST，求關鍵邊的時候只枚舉這個MST中的邊（其他的邊不可能在偽關鍵邊中）
• 使用kind數組記錄每條邊的屬性，在求完所有的關鍵邊以后再求偽關鍵邊，如果某條邊已經在一個MST中則直接加入偽關鍵邊（因為他不是關鍵邊，滿足偽關鍵邊的定義）

第二種我直接沒有看，因為Tarjan算法我已經忘光了，而且這道題好像還用到了kraskal算法的一個性質（并不知道

在Kruskal 算法中，對于任意的實數 w，只要我們將給定的邊按照權值從小到大進行排序，那么當我們按照順序處理完所有權值小于等于 w 的邊之后，對應的并查集的連通性是唯一確定的，無論我們在排序時如何規定權值相同的邊的順序。

感覺太難了，不想看了。

AC代碼

class Solution {
public:static constexpr int MAXN = 105;int father[MAXN];int kind[MAXN*MAXN];int m;  //邊數int value = 0;int root(int x) {return x == father[x] ? x : (father[x] = root(father[x]));}void merge(int u, int v) {father[root(u)] = root(v);}vector<int> critical_edges;vector<int> pseudo_critical_edges;/*** 求已經刪去第del條邊的圖的最小生成樹* 并差集的狀態為father* cnt用來記錄當前該最小生成樹中有多少條邊* ret用來記錄當前最小生成樹的權值和*/int kruskal(const int n, const vector<vector<int>> &edges, int del, int cnt, int ret) {for (int i = 0; i < m; ++i) {if (i == del) {//如果是已經刪除的邊，則跳過continue;}int u = edges[i][0];int v = edges[i][1];if (root(u) != root(v)) {merge(u, v);ret += edges[i][2];++cnt;if (kind[i] == -1 && del == -1)kind[i] = 0;    //表示該邊是某個最小生成樹的一條邊}}if (cnt == n-1) {//說明形成了最小生成樹return ret;} else {//說明原本不是一個連通分量return value + 122;}}static bool compare(const vector<int>& a, const vector<int>& b) {return a[2] < b[2];}vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {memset(kind, -1, sizeof(kind));m = edges.size();for (int i = 0; i < m; ++i) {edges[i].push_back(i);}sort(edges.begin(), edges.end(), compare);for (int i = 0; i < n; ++i) {//并查集的初始化father[i] = i;}value = kruskal(n, edges, -1, 0, 0);//尋找關鍵邊for (int i = 0; i < m; ++i) {if (kind[i] == -1) {//不是生成樹中的邊continue;}for (int i = 0; i < n; ++i) {//并查集的初始化father[i] = i;}int v = kruskal(n, edges, i, 0, 0);if (v > value) {//說明是關鍵邊kind[i] = 1;critical_edges.push_back(edges[i][3]);}}//尋找偽關鍵邊for (int i = 0; i < m; ++i) {if (kind[i] == 1) continue; //關鍵邊不可能是偽關鍵邊if (kind[i] == 0) {//如果在某個生成樹中還不是關鍵邊則一定是偽關鍵邊pseudo_critical_edges.push_back(edges[i][3]);continue;}//對于普通邊，首先將其加入到生成樹中，然后再判斷for (int i = 0; i < n; ++i) {//并查集的初始化father[i] = i;}merge(edges[i][0], edges[i][1]);int v = kruskal(n, edges, -1, 1, edges[i][2]);if (v == value) {//說明加入這條邊以后仍然能夠得到最小生成樹，是偽關鍵邊pseudo_critical_edges.push_back(edges[i][3]);}}return {critical_edges, pseudo_critical_edges};}
};

官方題解代碼

// 并查集模板
class UnionFind {
public:vector<int> parent;vector<int> size;int n;// 當前連通分量數目int setCount;public:UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {iota(parent.begin(), parent.end(), 0);}int findset(int x) {return parent[x] == x ? x : parent[x] = findset(parent[x]);}bool unite(int x, int y) {x = findset(x);y = findset(y);if (x == y) {return false;}if (size[x] < size[y]) {swap(x, y);}parent[y] = x;size[x] += size[y];--setCount;return true;}bool connected(int x, int y) {x = findset(x);y = findset(y);return x == y;}
};class Solution {
public:vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {int m = edges.size();for (int i = 0; i < m; ++i) {edges[i].push_back(i);}sort(edges.begin(), edges.end(), [](const auto& u, const auto& v) {return u[2] < v[2];});// 計算 valueUnionFind uf_std(n);int value = 0;for (int i = 0; i < m; ++i) {if (uf_std.unite(edges[i][0], edges[i][1])) {value += edges[i][2];}}vector<vector<int>> ans(2);for (int i = 0; i < m; ++i) {// 判斷是否是關鍵邊UnionFind uf(n);int v = 0;for (int j = 0; j < m; ++j) {if (i != j && uf.unite(edges[j][0], edges[j][1])) {v += edges[j][2];}}if (uf.setCount != 1 || (uf.setCount == 1 && v > value)) {ans[0].push_back(edges[i][3]);continue;}// 判斷是否是偽關鍵邊uf = UnionFind(n);uf.unite(edges[i][0], edges[i][1]);v = edges[i][2];for (int j = 0; j < m; ++j) {if (i != j && uf.unite(edges[j][0], edges[j][1])) {v += edges[j][2];}}if (v == value) {ans[1].push_back(edges[i][3]);}}return ans;}
};//作者：LeetCode-Solution
//鏈接：https://leetcode-cn.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/solution/zhao-dao-zui-xiao-sheng-cheng-shu-li-de-gu57q/
//來源：力扣（LeetCode）
//著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請注明出處。

仔細研究官方題解的代碼感覺收益頗多：

• 使用iota(begin, end, init)對數組進行初始化，其中init為初始值，需要能夠和++運算符結合
• 使用功能完善的并差集模板（我自己每次都是手寫，然后寫地支離破碎）
• 使用lamda表達式進行函數定義