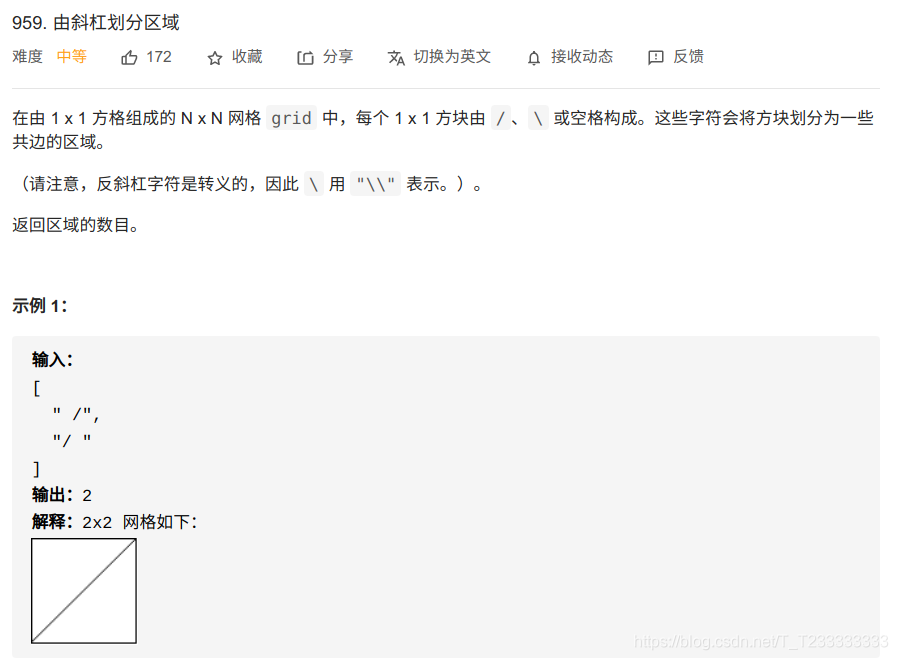
題目描述

題目分析

仔細分析這道題以后雖然覺得可能要轉化為圖之類的，但是完全沒有具體的想法，因為每個格子都有三種情況，這三種情況的不同的組合又會產生不同的結果。
發現找不到編碼轉化為圖以后，我分析了一下不同數量方塊之間的聯系，試圖找到像遞歸一樣的關系。發現也沒有找到，關鍵是邊長小的方塊四周會有邊，但是將其放到大方塊中并沒有這些邊，而且他們的邊界還會組合。
在沒有思路之后我看了一下題解，發現題解最巧妙的地方在于將每一個單元塊再次劃分為四個小塊，從而將原先三種情況統一了起來：每種情況是這四個小塊的不同組合方式。然后塊與塊之間同樣通過小塊進行拼接。然后再使用并差集得到聯通塊的個數。

總結

分解以后使用并查集得到聯通分量的個數這個是非常簡單的，但是關鍵在于分解這步自己沒有想到。以后遇到問題不應該僅僅思考問題的拼接、分類討論、遞歸，而且也應該考慮一下所謂的分類情況能否再進行分解從而將各種分類統一起來。

AC代碼

class UnionSet {
public:int n;int setCount;vector<int> father;vector<int> size;UnionSet(int _n):n(_n),setCount(_n),father(_n),size(_n, 1) {iota(father.begin(), father.end(), 0);}int root(int x) {//路徑壓縮return x == father[x] ? x : father[x] = root(father[x]);}bool unite(int x, int y) {x = root(x);y = root(y);if (x == y) {return false;}if (size[x] < size[y]) {//按秩合并swap(x, y);}father[y] = x;size[x] += size[y];--setCount;return true;}
};
class Solution {
public:int regionsBySlashes(vector<string>& grid) {int n = grid.size();UnionSet us(4 * n * n);for (int i = 0; i < n; ++i) {int idx = 0;    //用于指向對應的字符for (int j =0; j < n; ++j, ++idx) {int base = (i * n + j) * 4; //哈希值switch (grid[i][idx]) {case ' '://空格，將四個塊全部合并us.unite(base + 0, base + 1);us.unite(base + 0, base + 2);us.unite(base + 0, base + 3);break;case '/'://斜杠us.unite(base + 0, base + 3);us.unite(base + 1, base + 2);break;case '\\'://反斜杠us.unite(base + 0, base + 1);us.unite(base + 2, base + 3);//++idx;  //因為反斜杠有兩個break;}//完成和右邊塊和下邊塊的拼接if (j + 1 < n) {//右邊塊存在int baser = base + 4;us.unite(base + 1, baser + 3);}if (i + 1 < n) {//下邊塊存在int baseb = 4 * ((i + 1) * n + j);us.unite(base + 2, baseb + 0);}}}//最后聯通塊的個數return us.setCount;}
};

官方題解是用Java寫的，這里就不再貼出。剛開始看到題目中說反斜杠是兩個我還想著要對反斜杠特殊處理（代碼中的idx變量），結果真的只是編碼輸出的問題。。。