題目描述

輸入一個n行m列的整數矩陣，再輸入q個詢問，每個詢問包含四個整數x1, y1, x2, y2，表示一個子矩陣的左上角坐標和右下角坐標。

對于每個詢問輸出子矩陣中所有數的和。

輸入格式

第一行包含三個整數n，m，q。

接下來n行，每行包含m個整數，表示整數矩陣。

接下來q行，每行包含四個整數x1, y1, x2, y2，表示一組詢問。

輸出格式

共q行，每行輸出一個詢問的結果。

數據范圍

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
?1000≤矩陣內元素的值≤1000

輸入樣例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

輸出樣例：

17
27
21

解題思路

這道題就是二維前綴和

前綴和初始化

就是對于A i,j這個點，到它的和為

s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] +a[i][j]

前綴和遞推公式

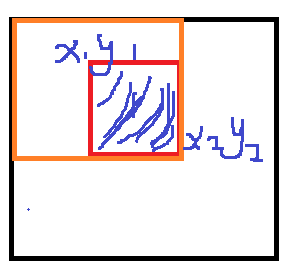
對于兩個點，x1,y1,x2,y2;他們的之間的和為

s[x2][y2] - s[x2][y1-1] - x[x1-1][y2] + s[x1-1][y1-1]

代碼實現

#include<iostream>
using namespace std;
const int N =1010;
int a[N][N],s[N][N];
int n,m,q;int main()
{scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&a[i][j]);//初始化前綴和for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];while(q--){int res = 0;int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);res = s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] +s[x1-1][y1-1];cout<<res<<endl;}return 0;
}