大三時候在跳蚤市場閑逛,從一位數學院的學長那里買了一些閑書,最近翻出來剛好有李榮華、劉播老師的《微分方程數值解法》和王仁宏老師的《數值逼近》,結合周善貴老師的《計算物理》課程,整理一下筆記。
本文整理常微分方程數值求解的歐拉法與龍格-庫塔法。
一般地,動力學系統的時間演化可以用常微分方程的初值問題來描述,例如設一維簡諧運動的回復力:
因此本文主要整理一階常微分方程初值問題的數值解法。
一階常微分方程初值問題
設
存在常數L,使得
假設
歐拉法
將區間
推導
1、根據泰勒展開式:
略去二階小量,得:
以此類推,得到遞推公式:
2、數值積分推導
由
以此類推,可得到:
為了提高精度,可以使用梯形積分代替矩形積分,即:
以此類推,得到改進的歐拉法:
Python計算實例
以
import math
from matplotlib import pyplot as pltt_0 = 0
y_0 = 1
tau = 0.1
i = 1
solve = []
Euler = []
t = []
while i < 100:if i == 1:y_n = y_0t_n = t_0Euler.append(y_n)solve.append(math.exp(t_n))t.append(t_n)func = y_ny_n = y_n + tau * funct_n = t_n + taui += 1plt.plot(t, Euler, c='green', label=' Euler method')
plt.plot(t, solve, c='red', label=' accuracy')
plt.fill_between(t, solve, Euler, facecolor='blue', alpha=0.2)
plt.title('Euler method', fontsize=19)
plt.xlabel('t', fontsize=19)
plt.ylabel('y', fontsize=19)
plt.legend()
plt.show()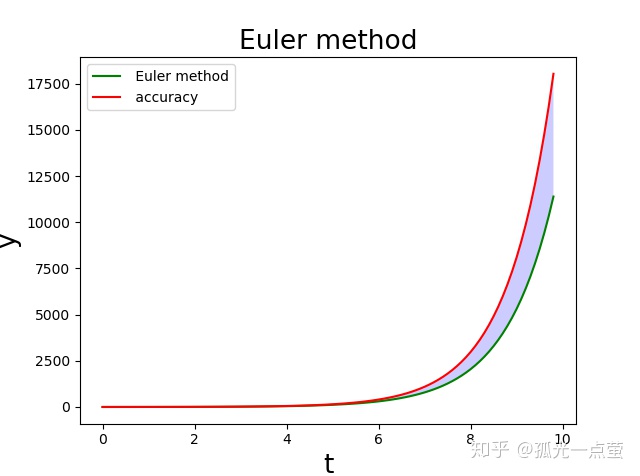
作圖可以看到,當迭代步數較多后,歐拉法的結果逐漸落后于精確指數解的增長速度。下面分析歐拉法的誤差來源。
在
在計算中,我們更關心精確解和數值解之間的誤差
根據Lipschitz條件,可得:
由
局部截斷誤差
穩定性分析
如果計算的初值不能精確給定,例如存在測量、舍入誤差等,在計算過程中,每一步傳遞的誤差連續依賴于初始誤差,則稱算法穩定,否則該算法不穩定。
對于不同的初值
兩式相減,得:
根據Lipschitz條件,可得:
龍格-庫塔法
龍格庫塔法的主要思想:在
將
令
以此類推,可以得到:
同時,我們可以寫出泰勒展開的形式解:
其中:
通項為:
基本思路是,利用當前點的函數值
現在把
將
將
與泰勒展開式
2個方程有3個未知數,因此有無窮多個解,可采用
令
此即為二階龍格-庫塔法。
與上一節的歐拉法公式對比:
Python計算實例
仍以
import math
from matplotlib import pyplot as pltt_0 = 0
y_0 = 1
z_0 = 1
tau = 0.1
i = 1
j = 1
solve = []
Euler = []
R_K = []
t = []
while i < 100:if i == 1:y_n = y_0t_n = t_0R_K.append(y_n)solve.append(math.exp(t_n))t.append(t_n)func_n = y_nfunc_m = y_n + tau * func_ny_n = y_n + 0.5 * tau * (func_n + func_m)t_n = t_n + taui += 1
t = []
while j < 100:if j == 1:z_n = z_0t_n = t_0Euler.append(z_n)t.append(t_n)func = z_nz_n = z_n + tau * funct_n = t_n + tauj += 1plt.scatter(t, R_K, marker='^', c='blue', s=70, label=' R-K method')
plt.plot(t, Euler, c='green', label=' Euler method')
plt.plot(t, solve, c='red', label=' accuracy')
plt.fill_between(t, solve, Euler, facecolor='yellow', alpha=0.2)
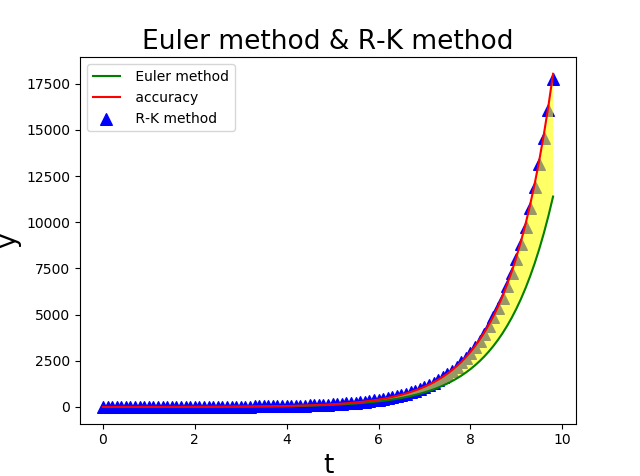
plt.title('Euler method & R-K method', fontsize=19)
plt.xlabel('t', fontsize=19)
plt.ylabel('y', fontsize=19)
plt.legend()
plt.show()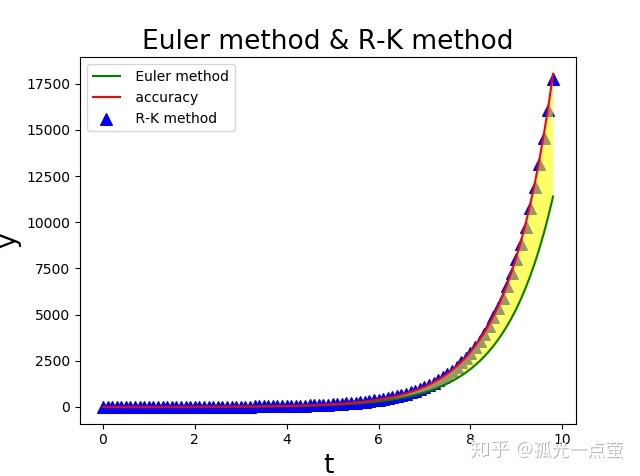
黃色部分表示數值解和精確解的偏離,可以看到,二階龍格-庫塔法(改進的歐拉法)精確度得到了很大的提升。
二階龍格-庫塔法中,泰勒展開到了
Reference:
1、周善貴,《計算物理》課程講義
2、李榮華,劉播,《微分方程數值解法》
3、王仁宏,《數值逼近》










)






)

