這里的知識來自于論文 Delving into the Devils of Bird’s-eye-view Perception: A Review, Evaluation and Recipe 的 Appendix B.1
部分來自 這篇文章

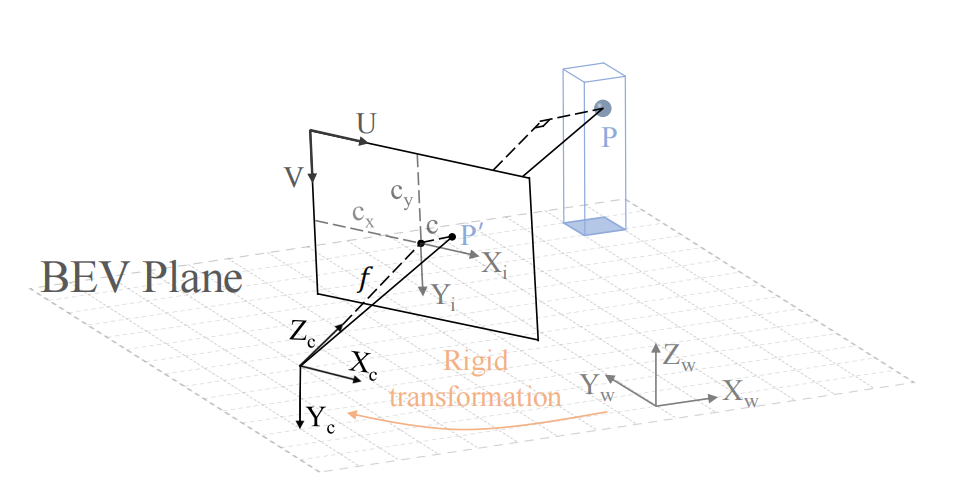
從透視圖轉向鳥瞰圖。（Xw、Yw、Zw）、（Xc、Yc、Zc）表示世界World坐標和相機Camera坐標，$（X_i、Y_i）$、（U、V）表示圖像坐標和像素坐標。由于圖像坐標系和像素坐標系處于同一平面，故兩者之間的差異在于坐標原點的位置和單位。像素坐標系的原點在圖像坐標系的左上角，同時像素坐標系的單位為像素。
故兩個坐標系之間的變換滿足
$u=\frac{x}{d_x}+u_0，v=\frac{y}{d_y}+v_0$
dx，dy表示像素坐標系中每個像素點的寬和高，而圖像坐標系原點在像素坐標系中的橫縱坐標分別為 $u_0,v_0$。
從BEV平面上升起一根柱子。P代表柱子上的3D點，$P^{{}^{\prime }}$代表P相應在相機視角上的投影點。
P，$P^{{}^{\prime }}$分別對應于柱上的三維點和攝像機視圖上投影的2D點。
給定P的世界坐標和相機的內在參數和外在參數，可以得到$P^{{}^{\prime }}$的像素坐標。

顯式BEV特征構造通常需要基于三維到二維投影對局部圖像視圖特征進行索引。上圖顯示BEVFormer的視角轉換。一根柱子從BEV平面升起，柱子內的一個三維點被投影到相機視圖上。
投影過程涉及到世界World、相機Camera、圖像Image和像素Pixel坐標系之間的轉換。
從世界坐標到相機坐標的轉換是一種剛性變換，只需要平移和旋轉（更詳細的可以看上面的博客）。
設$P_w=[x_w、y_w、z_w，1]、P_c=[x_c、y_c、z_c，1]$分別為一個三維點P在世界坐標和相機坐標中的同質表示。它們之間的關系可以描述如下：
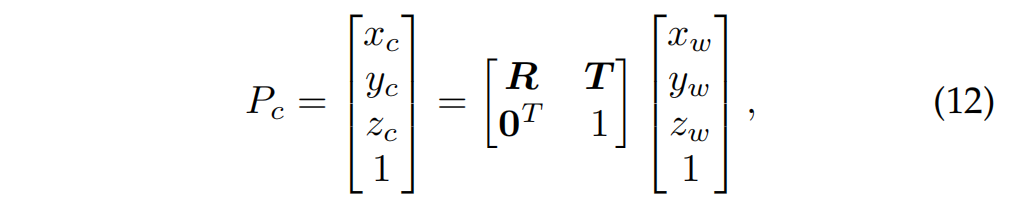R，T分別表示旋轉矩陣和平移矩陣。