轉載出處:https://blog.csdn.net/dog250/article/details/82177299
很明確地說,從通信意義上推敲,TCP一點都不可靠。一個抽象的協議,怎么可能左右介質來保證可靠,不存在的。但凡是經由某種介質的通信行為均不可能是絕對可靠的!
正好比我們現實生活中的保險,其實它什么都不能阻止,什么風險也保證不了它的不發生,它保證不了飛機不會掉下來,也無法阻止人生病…事實上,TCP就是通信中的保險業。
TCP是如何設計出來的?推而廣之這類通信協議是如何設計出來的?如果說讓你在一個不可靠的介質上運行一個可靠的協議,你該怎么做?本文將介紹內中的些許因果。
可靠的通信協議如何構建
這要從經典的兩軍問題說起。
首先介紹一下兩軍問題,來自Wiki的解說是最好的:
Two Generals’ Problem:https://en.wikipedia.org/wiki/Two_Generals%27_Problem
兩軍問題本質上一個一致性確認問題,也就是說通信雙方而不是一方(這對理解TCP非常重要)都要確保信息的一致性。即假設通信雙方為A和B,那么A發送一則消息M給B,所謂的可靠性則是要同時滿足下面的條件:
- 信道是不可靠的,任何消息均可能以任何概率丟失
- 如果AA不能確保消息到達對方時,不能重發消息
這一點非常重要,在經典的兩軍問題中,消息是由信使傳遞的,而信使是人,人是軍隊作戰的最重要資源也是最不可靠的資源,比如會叛變…因此每條消息或者確認相互只能派遣一個信使去遞送消息,在通信上講,就是消息不能重發! - 對于A而言,要確保A知道B已經收到了M
- 對于B而言,要確保自己收到M這件事已經被A知道
數學上很容易用反證法證明上述的兩軍問題是根本無解,即一致性通信的完全可靠性是一種奢望。下面我來試著推導一下。
假設在時間點TnTn的傳輸,我們知道,信道是不可靠的,所以它可能會丟失,而它一旦丟失,整個交互過程便失去了一致性,這與假設是矛盾的,所以,一致性是不可能的。
這個問題貌似徹底拆了通信技術的根基,那么通信技術還有什么意義呢?
事實上,
- 首先,通信協議從來都不是為了滿足完全的一致性需求
通信的意義是,在時間序列上滿足消息傳遞的單向完成需求即可!通信的本質問題是確保消息傳遞,而不是維護一致性,一致性應該由業務自身來負責,通信僅僅提供消息傳遞的基礎設施而已。
- 其次,通信傳輸的是字節電脈沖,消息可以重發
這便大大削弱了兩軍問題的強約束。基于上述的假設,我們來一步步地推導出TCP協議為什么要這么設計。
如果仔細推敲的話,你會發現,即便是消息傳遞,在數學上也是無法確保在不可靠的信道上確保消息傳遞的,然而,我們換個思路,即自問“信道到底不可靠到什么程度?”。
是100%不可靠嗎?如果是的話,意味著斷路,即雙方是不可達的,無論我們發送多少次數據包,均會丟失,這樣我們馬上可以結束這個沒有意義的討論,因此,所謂的不可靠只是說信道會出現概率性丟包,丟包概率pp之間的!
這個意義十分重大,這意味著,只要我們重試特定消息MnMn的確認!,這是完全確定的一個結論,沒人反對吧。
這邊自然而然導出了可靠通信的第一個原則:
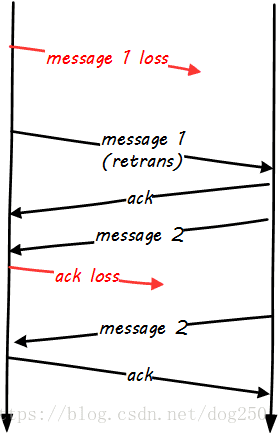
- 1.超時重傳
該原則可以確保消息一定能有機會到達對端。每當發出一個數據包,在預期的時間內沒有確認到達,就重傳它。關于超時重傳的細節,本文稍后會淺談一下,但是現在,我們來看另外一個問題。
如何確保消息單向傳遞的完成?
換句話說,所謂消息單向傳遞的完成,即需要一種標志性的信號*,該信號揭示了消息已經被對端接收這個事實,很顯然,對端發送針對特定消息的確認并且本端收到即可。
一旦AA,不然它也不會發送確認。但是由上文可知,這個確認在不可靠的信道上也可能丟失,不過這不必驚慌,因為我們已經有了推論,即針對任意消息,只要我們重復傳輸的次數足夠多,該消息就一定能到達對端,在該推論下,采用超時重傳原則即可。
現在看來,我們導出的下列措施已經解決了幾乎所有問題:
1. 針對消息MnMn的超時重傳機制
但是這是最優解嗎?
非也!這只是一種可行的方案,但不是唯一的方案,更不是最有的方案。導出最優解需要我們深入到通信網絡的本質,先看一篇文章:
馬太效應/冪律分布的本質以及其數學表述:https://blog.csdn.net/dog250/article/details/79146511
注意,我們的通信網絡是一個網狀拓撲的連通圖,無論是單節點連接數屬性還是流量屬性均符合冪律規律,從雙對數坐標曲線可以看出網絡規模和節點的各屬性特征之間的對數線性關系,而網絡規模來自于某種指數級增長的復制,單節點的屬性特征來自于該節點的行為,很顯然,在這個雙對數坐標下線性的通信網絡中,如果想等比例地縮放其規模而不至于崩潰,就必須用指數來控制單節點的行為(把雙對數坐標化為笛卡爾坐標即可展現)。
實際上,我們把雙對數坐標中的直線(求解微分方程的結果)展開到相應的笛卡爾坐標系,就是一條指數規律的曲線了。
再看另一個抽象,即如果數據包在傳輸過程中丟失了,這件事跟什么因素相關?誠然,在網絡通信中,這件事肯定有可能是和傳輸介質相關的,但是在節點數量,即網絡規模這個因素下,介質的問題可以忽略不計。也就是說,節點越多,傳輸越容易發生沖突,數據也就越不容易到達對端。即丟包事件和網絡規模相關,網絡是一個線性系統,所以,丟包的重傳必須具備指數級的時間特征。
介質的問題隨著網絡規模的擴大是線性增長的,而傳輸沖突的問題隨著網絡規模的擴大則是指數級的,孰重孰輕,立判!
如果你了解早期的以太網,即總線式的CSMA/CD以太網,你會發現同樣的事實。
因此,很明確,超時重傳的超時規則在線性系統的平衡通過指數特性的單獨節點行為來維持的原則下,則必須是:
- 2.超時重傳-指數退避
有了這個原則,我們再回過頭來看如何實現消息以及消息確認的超時重傳。直接說結論,即不對確認進行重傳,因為確認和消息本身屬于同一個行為,針對消息本身的超時重傳已經自動包含了一個確認,如果再針對確認進行重傳,就會破壞單點行為的指數特征,因此我們導出可靠通信的第三個特征:
- 3.不對確認進行超時重傳
由于我們僅僅想確保消息單向傳遞的可靠,即確保對端收到了本端發出的消息而無需讓對端知道這件事,第四個特征也隨即導出:
- 4.不對確認進行確認
基礎設施構建就此完畢,考慮到通信往往是雙向的,我們需要在其上構建一個可靠的雙向通信協議,怎么辦?
簡單,在另一端BB重新這么來一遍即可!于是我們觀察到,兩軍問題如果在超時重傳的前提下將雙向的消息傳遞和確認分解成兩個單向的消息傳遞和確認,事情就會簡單得多。
原始的兩軍問題解法:
轉換后的解法:
嗯,轉換后的解法,即我們熟悉的協議,TCP協議的最基本形式。現在進入TCP時間!
TCP握手,揮手,一致性的問題
經常有人問,TCP為什么是3次握手,而不是2次,也不是4次,5次。知乎上經常會有這種問題,但是答案幾乎是千篇一律的錯誤或者答非所問,最常見的答案只是描述一下TCP握手的細節,然后導出這么做是OK的,其實不這么做也是OK的這一點沒人提。
最常見的錯誤答案:
1. 這是一種權衡,因為無數次握手也不可能完全可靠;
2. 描述握手的協議細節;
3. …
看過了我上面的論述,這個問題應該非常好答了,所謂的TCP建立連接的握手,實質上就是建立一個雙向的可靠通信連接,一邊一個來回,每一邊都自帶超時重傳來確保可靠性(而不是靠握手的次數)。TCP的3次握手是優化的結果,其實它應該是4次握手,由于是從零開始的建立連接,因此將SYN的ACK以及被動打開的SYN合并成了一個SYN-ACK,僅此而已。
握手的作用,旨在確定兩個雙向的初始序列號,TCP用序列號來編址傳輸的字節,由于是兩個方向的連接,所以需要兩個序列號,握手過程不傳輸任何字節,僅僅確定初始序列號:
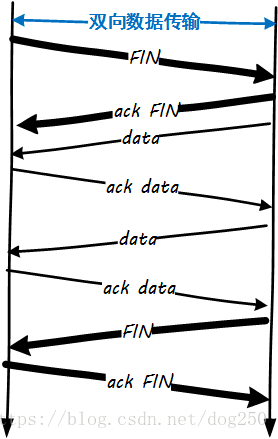
說完了3次握手,那么,其姊妹問題,為什么TCP的斷鏈是4次揮手而不是3次?
換句話說,即是在問為什么針對主動斷開方的FIN的ACK以及本端的FIN不能合并?
非常簡單,因為TCP是在一個單向可靠通信系統基礎上構建而成的雙向傳輸控制協議,握手期間可以合并ACK和SYN,是因為在握手之前兩端沒有任何連接上的包袱,而在斷鏈揮手時,一端認為可以斷開了,另一端卻不一定,可能另一端還有數據要傳輸,所以便不能合并,被動關閉的一方只能單獨處理針對FIN的ACK以及自己的FIN,僅此而已。
再來一個問題,TCP能確保一致性嗎?換句話說,TCP協議是兩軍問題的一個解嗎?
遠遠不是!TCP并不確保一致性。
任何時間點,TCP都不能完全確認當前時刻連接雙方的狀態,此處所謂的狀態包括兩端傳輸的數據。一致性是基于消息的,而不是基于連接的!也就是說,TCP只有收到下一個數據包時,才知道上一個數據包的接收情況,而無法實現隔空打人!TCP的好處僅在于,它在一個信息流上實現了一個一致性確認的流水線方式。
我們在理解這個流水線方式的時候,不應該考慮滑動窗口,那樣會比較難以理解,我們應該僅僅考慮單字節停等機制。事實上也確實是這樣,滑動窗口機制只是為流量控制而引入的,單字節停等效率又太低,所以說這并無傷大雅,你把字節換成窗口即可,即單窗口停等。
如果我們把一致性推廣到連接的層面,在連接層面,一致性就是靠4次揮手保證的。
我們可以看到,4次揮手那里的狀態機非常之復雜,這是有原因的,即便是引入了TIMEWAIT狀態,也還是沒有辦法保證徹底的一致性,這是兩軍問題本質上不可解的一個結論,僅此而已。
1974年的TCP
現在你應該大致知道TCP如何保證可靠性了,進一步,如果你想知道TCP協議的頭部為什么是那個樣子,這一切是如何安排的,你就不得不去讀一下一篇陳年的論文:
《A Protocol for Packet Network Intercommunication》:https://www.cs.princeton.edu/courses/archive/fall08/cos561/papers/cerf74.pdf
我來大致介紹一下這篇劃時代的論文。
毫不夸張地說,該論文奠定了以TCP/IP為核心的互聯網的基礎,我們今天能刷抖音,用微信聊天,能在線看片…這一切要不是這篇論文,不會是現在這個樣子。
該論文的重點不是TCP協議,而是TCP/IP作為一個整體如何發揮作用,早在1974年,分層模型還不算太成熟,所以當我們提起TCP/IP的時候,要明白,最初的時候,這兩個協議是牢牢切合在一起的,到了后來為了兼容純IP轉發,才加入了UDP,這個時候,人們意識到分層模型的必要性。于是抽象而成的ISO/OSI模型。
該論文主要有兩個論題:
- 網關的概念和意義–最終的IP協議
- 進程間通信的傳輸控制–最終的TCP協議
注意,我們看看TCP最初的形式,沒錯,它是作為一種進程間通信的手段被提出的,當初TCP作為進程間通信手段,側重于不同主機的進程間通信,因此,我們可以清晰看到它的API和文件IO的API是多么相似,這也是socket可以作為文件描述符的原因。
此外,還有值得注意的是,TCP的ACK號被定義為下一個索要字節的序列號,這在當時實現了一種簡易且完備的字節流水線,節省了協議頭空間,看到這個設計,簡直太帥!雖然它也帶來了很多問題,比如無法精確測準RTT,比如無法進行選擇確認,進而無法進行良好的擁塞控制,但不得不說,在空間重于時間的1970年代,這絕對是創舉,畢竟,擁塞控制在當時是沒有意義的,1988年才被引入。
1974年的互聯網
在1974年那篇論文之后,同樣的作者歸納總結出了RFC675:
《RFC675:SPECIFICATION OF INTERNET TRANSMISSION CONTROL PROGRAM》:https://tools.ietf.org/html/rfc675
這篇劃時代的RFC正式提出了互聯網這個概念,我們常說的Internet就是Internetworking的縮寫。
TCP/IP協議確實不是一個協議棧,最初它們只是一個協議,僅此而已,不多說。
…
那么,接下來?
接下來,skinshoe wu來了,攜帶著他的高級皮鞋,還有高級西裝。








完畢時,堆所對應的二叉樹中序遍歷序列為)
進行一趟歸并后的結果為)











