文章目錄

4、多層感知機（ MLP）
- 4.1、多層感知機
- - 4.1.1、隱層
  - 4.1.2、激活函數 σ
- 4.2、從零實現多層感知機
- 4.3、簡單實現多層感知機
- 4.4、模型選擇、欠擬合、過擬合
- 4.5、權重衰退
- 4.6、丟失法|暫退法（Dropout）
- - 4.6.1、dropout 函數實現
  - 4.6.2、簡潔實現
- 4.7、數值穩定性

4、多層感知機（ MLP）

4.1、多層感知機

加入一個或多個隱藏層+激活函數來克服線性模型的限制，使其能處理更普遍的函數關系類型，這種架構通常稱為多層感知機（multilayer perceptron）。

輸入層不涉及任何計算，因此使用此網絡產生輸出只需要實現隱藏層和輸出層的計算。

在這里插入圖片描述

4.1.1、隱層

通用近似定理

多層感知機可以通過隱藏神經元，捕捉到輸入之間復雜的相互作用，這些神經元依賴于每個輸入的值。多層感知機是通用近似器，即使是網絡只有一個隱藏層，給定足夠的神經元和正確的權重，可以對任意函數建模。

通過使用更深（而不是更廣）的網絡，可以更容易地逼近許多函數。

4.1.2、激活函數 σ

激活函數（activation function）通過計算加權和并加上偏置來確定神經元是否應該被激活，換句話說，激活函數的目的是引入非線性變化。

常見激活函數

ReLU 是絕大多數情況的選擇。原因是它計算簡單，不用跑指數運算，CPU跑指數運算是很費時間的，GPU會好一些。

1）ReLU

$R e LU (x) = ma x (x, 0)$

使用 ReLU 的原因是，它求導表現得特別好：要么讓參數消失，要么讓參數通過。這使得優化表現得更好，并且ReLU減輕了困擾以往神經網絡的梯度消失問題目前還不理解，為什么這樣優化表現更好？

2）Sigmoid

$\frac{1}{1+e^{-x}}$

它將范圍（-inf, inf）中的任意輸入壓縮到區間（0, 1）中的某個值。

3）tanh

$\frac{1-e^{-2x}}{1+e^{-2x}}$

將其輸入壓縮轉換到區間(-1, 1)上。

為什么要引入非線性變換？

非線性變換比線性變換有更強的表達能力。可逼近任意復雜函數，更加貼合真實世界問題，現實世界中單調、線性是極少存在的。

例如，如果我們試圖預測一個人是否會償還貸款。我們可以認為，在其他條件不變的情況下，收入較高的申請人比收入較低的申請人更有可能償還貸款。但是，雖然收入與還款概率存在單調性，但它們不是線性相關的。收入從0增加到5萬，可能比從100萬增加到105萬帶來更大的還款可能性。處理這一問題的一種方法是對我們的數據進行預處理，使線性變得更合理，如使用收入的對數作為我們的特征。(該例來自 DIVE INTO DEEP LEARNING)

softmax 函數與隱層激活函數的區別？

softmax 函數主要用于輸出層，而不是隱藏層。隱藏層的激活函數通常是為了引入非線性，而 softmax 函數則是為了將得分映射為概率，用于多分類問題的輸出。

什么是層數塌陷？

梯度消失。

4.2、從零實現多層感知機

（損失函數、優化算法來自 torch）

import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型參數

num_inputs, num_outputs, num_hiddens = 784, 10, 256
#生成了一個服從標準正態分布（均值為0，方差為1）的隨機張量 大小(num_inputs, num_hiddens)，作為 w 初始值。
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
# 大小為(num_hiddens,)的零張量 ，作為 b 的初始值 
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))params = [W1, b1, W2, b2]

權重為什么要乘 0.01？

乘以0.01的目的是將初始權重縮放到一個較小的范圍，以便更好地初始化網絡。

激活函數

def relu(X):# 創建了一個與輸入張量X具有相同形狀的全零張量aa = torch.zeros_like(X)return torch.max(X, a)

定義模型

def net(X):# -1 表示該維度將根據張量的大小自動計算， 如：784， reshape(-1,28) 會得到28*28X = X.reshape((-1, num_inputs))H = relu(X@W1 + b1)  # 這里“@”代表矩陣乘法return (H@W2 + b2)

損失函數

# reduction='none'：表示不進行降維，張量的形狀通常與輸入的標簽張量的形狀相同。
loss = nn.CrossEntropyLoss(reduction='none')

訓練 & 優化算法

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

評估

d2l.predict_ch3(net, test_iter)

4.3、簡單實現多層感知機

import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),nn.Linear(256, 10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights);

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4.4、模型選擇、欠擬合、過擬合

模型選擇

DL 的核心是，設計一個大的模型，控制它的容量，盡可能地降低泛化誤差。

泛化誤差(test_loss)：模型在新數據上的誤差。

訓練誤差（train_loss）：模型在訓練數據上的誤差，反映了模型在訓練數據上的擬合程度。

模型訓練過程中用到的損失是 train_loss 。

測試集：只用一次的數據集【如競賽提交后才進行測試的無法用于調超參數的不可知數據】。

驗證集：用來評估模型好壞的數據集，根據結果調整超參數。

小數據集上做驗證，通常使用K-則交叉驗證，常用k=5或10。
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42)這種分割之后，哪里涉及到驗證損失？繪制出來的 test_loss 算測試損失還是驗證損失？

沐神提到過，數據集分割中的X_test,y_text 是當作測試集實際上是驗證集（val），不代表模型在新數據上真實泛化能力。
對上方紅字，我的理解：數據集分割的test，在使用時確實是當測試集對待的，對代碼來說他就是測試集，但是在代碼之外，往往會根據這個結果人為地去調整下學習率、隱層節點之類的超參數，那么就更加貼合驗證集的定義，是實際中的驗證集。
所以翻閱書籍看到 test 就應該啊理解為測試集，不要鉆牛角尖說事實上我壓根就沒有測試集，到我手上了的都成為驗證集了，因為我后續會調參，薛定諤的貓。所以書籍教程上談 test為測試集，沒有任何問題（一直糾結很久，所以記錄一下）。

超參數：訓練前預定義好的，訓練中不會變，（lr、epoch、batchsize、正則化參數、隱層節點數）。

參數：權重w、偏移量b之類的。

過擬合&欠擬合

低容量配簡單數據時，高容量模型配復雜數據時，擬合正常。
高容量模型數據少，容易過擬合；低容量模型數據復雜，易欠擬合。
模型容量

擬合各種函數的能力，高容量的模型可以記住所有訓練數據。

如何估計模型容量？
- 參數個數
- 參數值的選擇范圍
VC維（Wapnik-Chervonenkis dimension）是統計學提供的量化模型容量的方法，提供一個為什么一個模型好的理論依據。在DL中使用VC維很困難。

（圖片來自《DIVE INTO DEEP LEARNING》）

數據復雜度

樣本數、沒樣本元素數、時空結構、多樣性。
更多的，模型容量和數據復雜度是直觀感受，不斷積累調參得來的感受。

4.5、權重衰退

權重衰減是最廣泛使用的正則化的技術之一，它通常也被稱為 $L_2正則化$ 。

正則化是處理過擬合常用方法，在訓練集損失函數中加入懲罰項，以降低模型復雜度。保持模型簡單的一個特別的選擇是使用 $L_2懲罰$ 的權重衰減。

常見的正則化方法：

L1 正則化（L1 Regularization）：在損失函數中添加參數的絕對值之和，即 L1 范數。這將導致一些參數變為零，從而實現特征選擇的效果，使得模型更稀疏。
L2 正則化（L2 Regularization）：在損失函數中添加參數的平方和的一半，即 L2 范數。這會使模型的參數更加平滑，防止參數過大，從而減輕過擬合。
Elastic Net 正則化：結合了 L1 和 L2 正則化，同時對參數施加 L1 和 L2 懲罰項。
Dropout 正則化：在訓練過程中，隨機地將一些神經元的輸出設置為零，以降低神經網絡的復雜性。
數據增強（Data Augmentation）：通過對訓練數據進行一系列隨機變換（如翻轉、旋轉、縮放等），增加數據樣本，從而提高模型的泛化能力。

參數更新法則

計算梯度

$\frac{?}{?w}(L(w,b) + \frac{λ}{2}||w||^2) = \frac{?L(w,b)}{?w} + \lambda w$

更新參數（時間t）

$η\frac{?L(w,b)}{?w}$

通常 $η\lambda < 1$ ，深度學習中這個就叫做權重衰減。

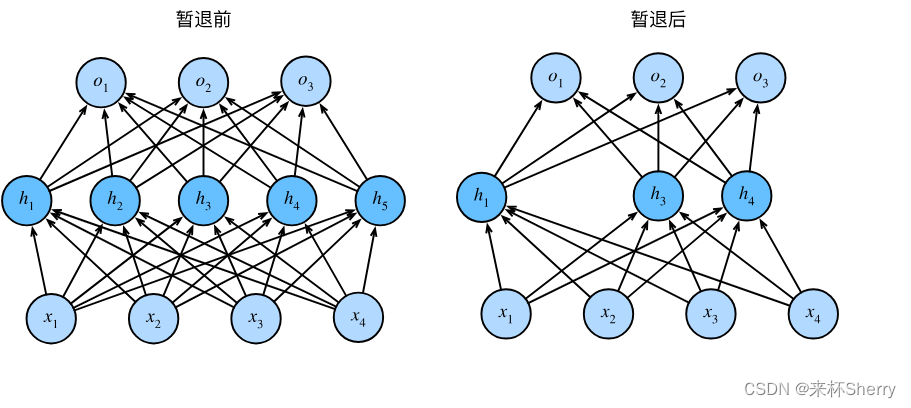
4.6、丟失法|暫退法（Dropout）

Dropout 是一種常用的正則化技術，正則技術就是用于防止神經網絡過擬合。

丟棄法將一些輸出項隨機置0來控制模型復雜度，常作用在多層感知機的隱藏層輸出上，丟棄概率是控制模型復雜度的超參數。

常用 dropout rate = 0.5 or 0.9 or 0.1

無偏差的加入噪音

對 $x$ 加入噪音得到 $x^{'}$ ，我們希望

$E [x^{'}] = x$

丟棄法對每個元素進行如下擾動

$x_i' = \begin{cases} 0& \text{with probability p} \\ \frac{x_i}{1-p} &\text{otherise} \end{cases}$

怎么能看出"加噪音"這個動作，這不是"丟棄"動作嗎？

理論上 dropout 是在做一個隱層之間加噪音的操作，實際上是通過上述 $x$ 轉 $x^{'}$ 實現的。

丟棄法的實際使用

通常將丟棄法作用于隱層的輸出上。

[hidden layers]

? ↓

[dropout layer]

? ↓

[output layer]

$h = σ(W_1x + b_1)$

$h^{'} = d ro p o u t (h)$

$o = W_2h' + b_2$

$y = so f t ma x (o)$

（圖片來自《DIVE INTO DEEP LEARNING》）

4.6.1、dropout 函數實現

import torch 
from torch import nn
from d2l import torch as d2ldef dropout_layer(X,dropout):#dropout只有在合理范圍內，斷言允許繼續執行assert 0 <= dropout <=  1# dropout =1 分母無意義if dropout ==1:return torch.zeros_like(X)if dropout == 0:return Xmask = (torch.rand(X.shape) > dropout ).float()return mask * X / (1.0 - dropout)

4.6.2、簡潔實現

在每個全連接層之后添加一個Dropout層

net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),# 在第一個全連接層之后添加一個dropout層nn.Dropout(dropout1),nn.Linear(256, 256),nn.ReLU(),# 在第二個全連接層之后添加一個dropout層nn.Dropout(dropout2),nn.Linear(256, 10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights);

訓練和測試

trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

4.7、數值穩定性

參數初始化重要性：影響梯度和參數本身的穩定性

梯度計算的是矩陣與梯度向量的乘積，最初矩陣可能具有各種各樣的特征值，他們的乘積可能非常大也可能非常小。

不穩定梯度帶來的風險不止在于數值表示；不穩定梯度也威脅到我們優化算法的穩定性。梯度爆炸，參數更新過大，破壞模型穩定收斂；梯度消失，參數更新過小，模型無法學習。

當網絡有很多層時，sigmoid函數的輸入很大或是很小時，它的梯度都會消失，激活函數會選擇更穩定的ReLU系列函數。

參數對稱性

神經網絡設計中的另一個問題是其參數化所固有的對稱性。假設我們有一個簡單的多層感知機，它有一個隱藏層和兩個隱藏單元。在這種情況下，我們可以對第一層的權重 $W^{(1)}$ 進行重排列，并且同樣對輸出層的權重進行重排列，可以獲得相同的函數。第一個隱藏單元與第二個隱藏單元沒有什么特別的區別。換句話說，我們在每一層的隱藏單元之間具有排列對稱性。