利用蒙特.卡羅方法計算圓周率近似值

什么是蒙特.卡羅方法？
答：蒙特卡羅方法是一種計算方法。原理是通過大量隨機樣本，去了解一個系統，進而得到所要計算的值。
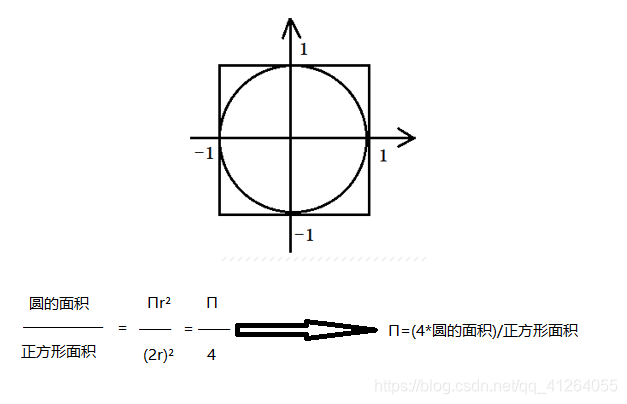
正方形內部有一個相切的圓，它們的面積之比是π/4。
這里假設正方形的邊長為2，也就是[-1,1]之間

from random import randomdef estimatePI(times):hits = 0for i in range(times):x = random()*2 – 1 #random()生成介于0和1之間的小數y = random()*2 - 1 #該數字乘以2再減1，則介于-1和1之間if x*x + y*y <= 1:       #落在圓內或圓周上hits += 1return 4.0 * hits/times
#這里的times為正方形的面積，hits為圓的面積，當正方形的面積越來越大的時候，Π = 4.0 * hits/times的值越精確
print(estimatePI(10000))
print(estimatePI(1000000))