b tree和b+tree

B TREE及其操作簡介 (Introduction to B TREE and its operations)

A B tree is designed to store sorted data and allows search, insertion and deletion operation to be performed in logarithmic time. As In multiway search tree, there are so many nodes which have left subtree but no right subtree. Similarly, they have right subtree but no left subtree. As is known, access time in the tree is totally dependent on the level of the tree. So our aim is to minimize the access time which can be through balance tree only.

B樹設計用于存儲排序的數據，并允許在對數時間內執行搜索，插入和刪除操作。 就像在多路搜索樹中一樣，有許多節點具有左子樹但沒有右子樹。 同樣，它們具有右子樹，但沒有左子樹。 眾所周知，樹中的訪問時間完全取決于樹的級別。 因此，我們的目標是最大程度地減少只能通過平衡樹訪問的時間。

For balancing the tree each node should contain n/2 keys. So the B tree of order n can be defined as:

為了平衡樹，每個節點應包含n / 2個鍵。 因此，n階的B樹可以定義為：

1. All leaf nodes should be at same level.

   所有葉節點應處于同一級別。

2. All leaf nodes can contain maximum n-1 keys.

   所有葉節點最多可以包含n-1個密鑰。

3. The root has at least two children.

   根至少有兩個孩子。

4. The maximum number of children should be n and each node can contain k keys. Where, k<=n-1.

   子代的最大數量應為n，每個節點可以包含k個鍵。 其中，k <= n-1。

5. Each node has at least n/2 and maximum n nonempty children.

   每個節點至少具有n / 2個，最多n個非空子代。

6. Keys in the non-leaf node will divide the left and right sub-tree where the value of left subtree keys will be less and value of right subtree keys will be more than that particular key.

   非葉節點中的鍵將劃分左右子樹，其中左子樹鍵的值將小于該左子樹，而右子樹鍵的值將大于該特定鍵。

Let us take a B-tree of order 5,

讓我們以5階的B樹為例

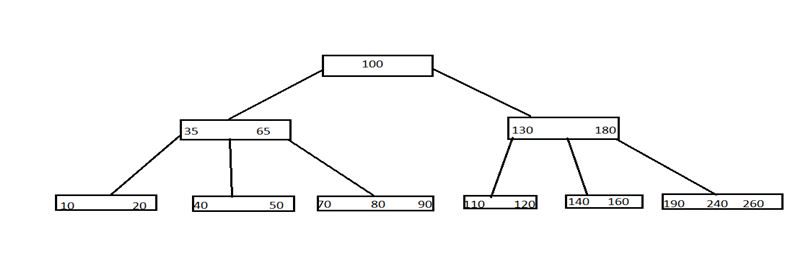
Here, we can see all leaf nodes are at same level. All non-leaf nodes have no empty sub-tree and they have keys 1 less than the number of their children.

在這里，我們可以看到所有葉節點處于同一級別。 所有非葉節點都沒有空的子樹，并且它們的鍵數比其子節點數少1。

B樹上執行的操作 (Operations performed on B Tree)

1. Insertion in B-Tree

   插入B樹

2. Deletion from B-Tree

   從B樹刪除

1)插入B樹 (1) Insertion in B-Tree)

The insertion of a key in a B tree requires the first traversal in B-tree. Through the traversal, it is easy to find that key which needs to be inserted is already existed or not. There are basically two cases for inserting the key that are:

在B樹中插入密鑰需要在B樹中進行第一次遍歷。 通過遍歷，很容易發現需要插入的密鑰已經存在或不存在。 基本上有兩種插入密鑰的情況：

1. Node is not full

   節點未滿

2. Node is already full

   節點已滿

If the leaf node in which the key is to be inserted is not full, then the insertion is done in the node.

如果要插入密鑰的葉節點未滿，則在該節點中完成插入。

If the node were to be full then insert the key in order into existing set of keys in the node, split the node at its median into two nodes at the same level, pushing the median element up by one level.

如果節點已滿，則按順序將密鑰插入節點中現有的密鑰集中，將節點的中值拆分為同一級別的兩個節點，將中值元素向上推一個級別。

Let us take a list of keys and create a B-Tree: 5,9,3,7,1,2,8,6,0,4

讓我們獲取一個鍵列表并創建一個B樹：5,9,3,7,1,2,8,6,0,4

1) Insert 5

1)插入5

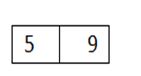
2) Insert 9: B-tree insert simply calls B tree insert non-full, putting 9 to the right of 5.

2)插入9 ：B樹插入簡單地調用B樹插入不完整，將9放在5的右邊。

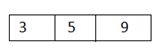
3) Insert 3: Again B-tree insert non-full is called

3)插入3 ：再次調用非完整的B樹插入

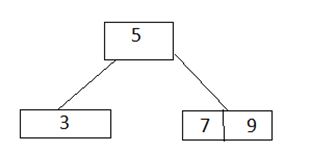
4) Insert 7: Tree is full. We allocate a new empty node, make it the root, split a former root, and then pull 5 into a new root.

4)插入7 ：樹已滿。 我們分配一個新的空節點，將其設為根，拆分先前的根，然后將5拉入新的根。

5) Insert 1: It goes with 3

5)插入1 ：與3對應

6) Insert 2: It goes with 3

6)插入2 ：與3對應

7) Insert 8, 6: As firstly 8 goes with the 9 and then 6 would go with 7, 8, 9 but that node is full. So we split it bring its middle child into the root.

7)插入8、6 ：首先8與9并存，然后6與7、8、9并存，但該節點已滿。 因此，我們將其拆分為中間孩子。

8) Insert 0, 4: 0 would go with the 1, 2, and 3 which are full, so we split it sending the middle child up to the root. Now it would be nice to just stick 4 in with 3, but the B-tree algorithm requires us to split the full root. Now we can insert 4 assured that future insertion will work.

8)插入0、4 ：0將與1、2和3充滿，因此我們將其拆分，將中間子級發送到根。 現在將4和3堅持下去會很好，但是B樹算法要求我們拆分完整的根。 現在我們可以插入4，確保將來的插入將起作用。

2)從B樹刪除 (2) Deletion from B Tree)

Deletion of the key also requires the first traversal in B tree, after reaching on a particular node two cases may be occurred that are:

刪除密鑰還需要在B樹中進行第一次遍歷，到達特定節點后可能會發生兩種情況：

1. Node is leaf node

   節點是葉節點

2. Node is non leaf node

   節點是非葉節點

Example: Let us take a B tree of order 5

示例：讓我們采用5階B樹

1) Delete 190: Here 190 is in leaf node, so delete it from only leaf node.

1)刪除190 ：此處的190位于葉節點中，因此僅從葉節點中將其刪除。

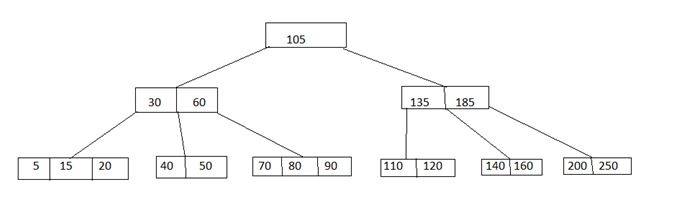
2) Delete 60: Here 60 is in non leaf node. So first it will be deleted from the node and then the element of the right child will come in that node.

2)刪除60 ：這里60在非葉節點中。 因此，首先將其從節點中刪除，然后右子元素將進入該節點。

B樹的應用 (Applications of B Tree)

The main application of a B tree is the organization of a huge collection of a data into a file structure. In this insertion, deletion and modification can be carried out perfectly and efficiently.

B樹的主要應用是將龐大的數據集合組織到文件結構中。 通過這種插入，可以完美而有效地進行刪除和修飾。

Full, so we split it sending the middle child up to the root. Now it would be nice to just stick 4 in with 3, but the B-tree algorithm requires us to split the full root. Now we can insert 4 assured that future insertion will work.

已滿，因此我們將其拆分，將中間孩子發送到根。 現在將4和3堅持下去會很好，但是B樹算法要求我們拆分完整的根。 現在我們可以插入4，確保將來的插入將起作用。

翻譯自: https://www.includehelp.com/data-structure-tutorial/introduction-to-b-tree.aspx

b tree和b+tree