圖像分割-閾值處理詳解(迭代法、Otsu法、平滑改善法、邊緣改進法、分塊處理法、局部特性法、移動平均法)

博主聯系方式：
QQ:1540984562
QQ交流群：892023501
群里會有往屆的smarters和電賽選手，群里也會不時分享一些有用的資料，有問題可以在群里多問問。

閾值處理詳解

    • 基礎：
    • 基于全局的閾值處理
      • 1迭代算法（最小概率誤判）
      • 2基于Otsu最佳全局閾值方法（非常有效）
      • 3用圖像平滑改善全局閾值處理
      • 4利用邊緣改進全局閾值處理
    • 基于局部的閾值處理
      • 1圖像分塊可變閾值處理
      • 2基于局部圖像特性的可變閾值處理
      • 3基于移動平均法的可變閾值

基礎：

首先將灰度圖轉化成灰度直方圖，橫坐標是灰度值（0-255），縱坐標是像素個數。（歸一化之后表征的是像素出現的概率）
如下圖所示：
灰度直方圖性質：
灰度直方圖性質
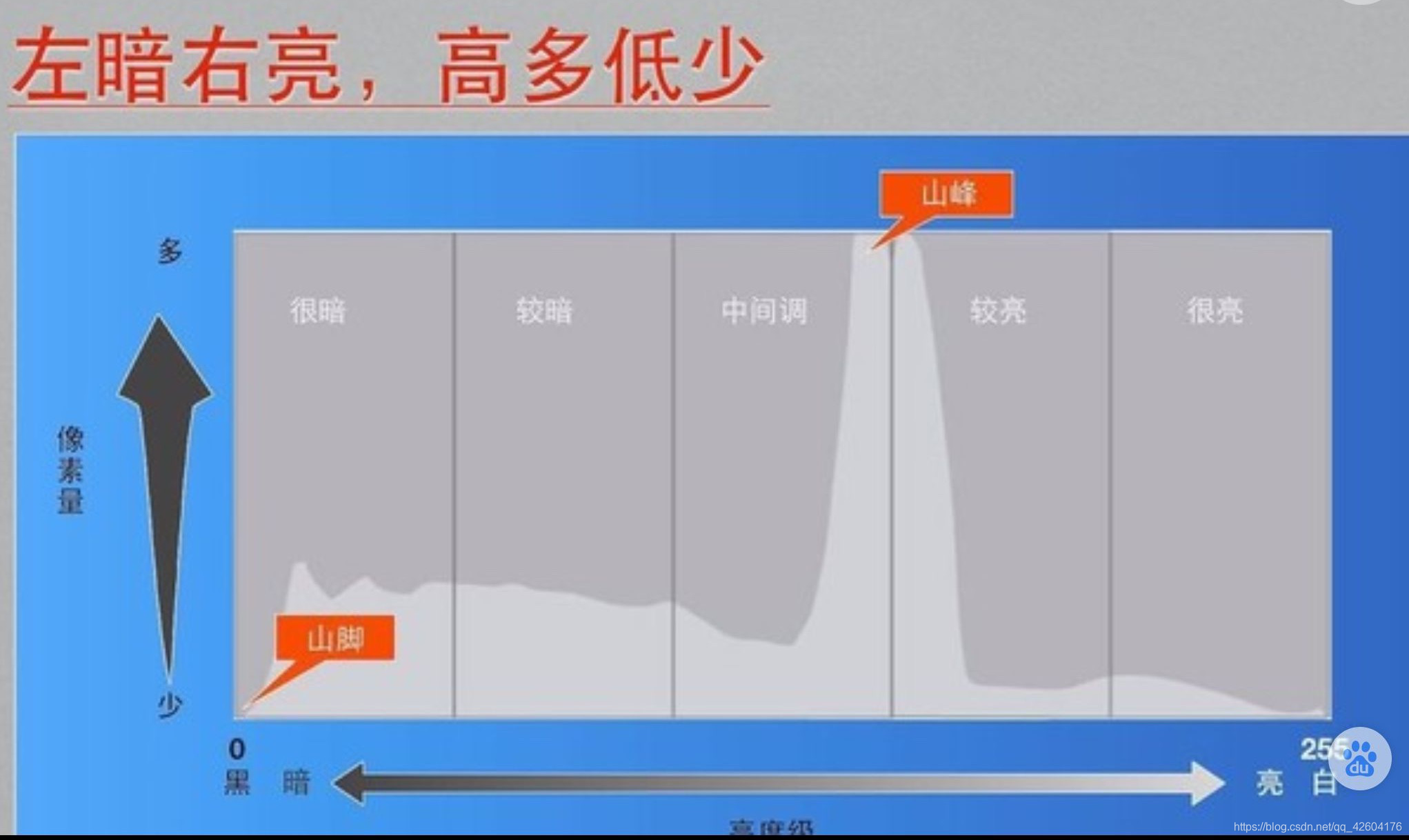
兩幅灰度直方圖兩幅灰度直方圖
如圖，從圖A可以看出，直方圖有兩個明顯的波峰和一個明顯的波谷，表明灰度普遍分為兩個密集區域。此時將門限設置在兩者之間的波谷，則可以很好地分割出背景和物體。
同理，觀察圖B，有三個明顯的波峰和兩個明顯的波谷，此時可以設置雙門限，將圖像分割為三類，如下圖冰山就是很好的例子，分割為暗背景、冰山的明亮區域和陰影區域。
冰山
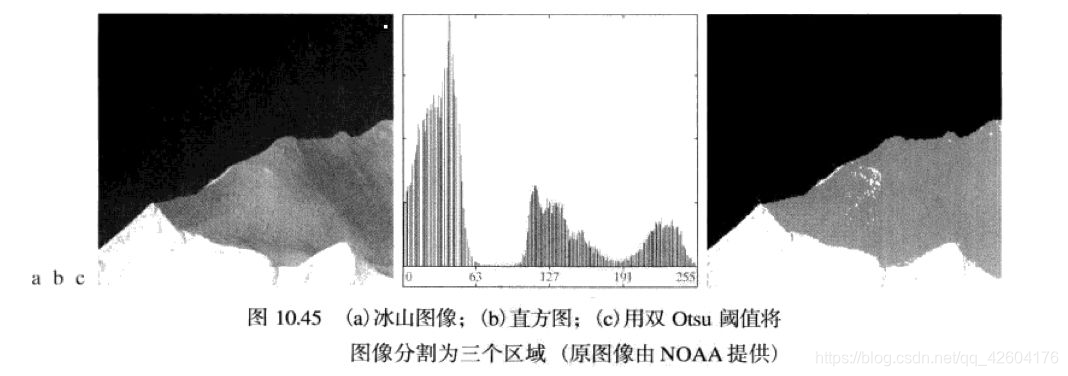
然而并不是所有圖像的直方圖都是有明顯的多個波峰和波谷的。
單峰型：
單峰型

無明顯波谷型
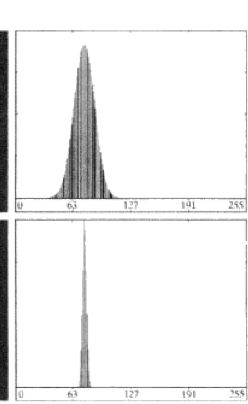
無明顯波谷型

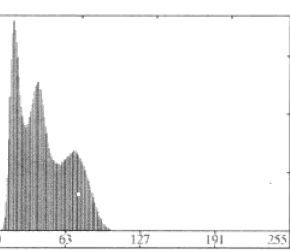
灰度趨于一致型（被噪聲污染過）
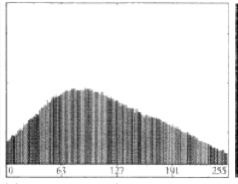
灰度趨于一致型

灰度閾值取決于波谷的寬度和深度，影響波谷特性的關鍵因素有：
1、波峰的間隔（波峰離得越遠，分離這些模式機會越好）
2、圖像中的噪聲內容（模式隨噪聲的增加而展寬）
3、物體和背景的相對尺寸
4、光源的均勻性
5、圖像反射的均勻性

接下來的所有的閾值處理方法，其目的都是：將灰度直方圖變得好處理 并 找到分割背景和物體的門限灰度值。

基于全局的閾值處理

1迭代算法（最小概率誤判）

公式推導：
1
2
3
4
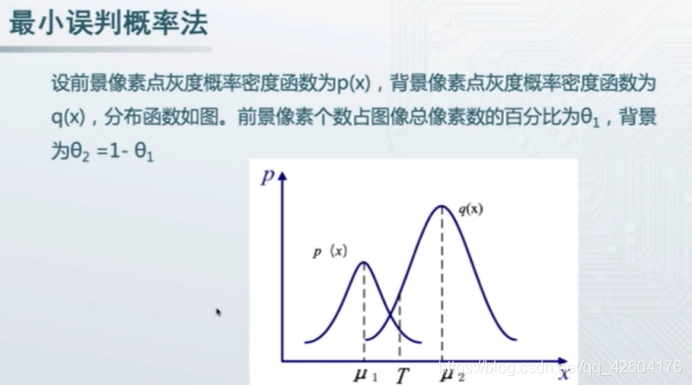
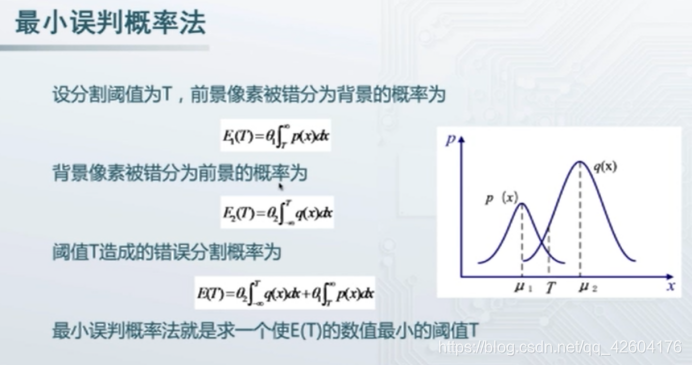
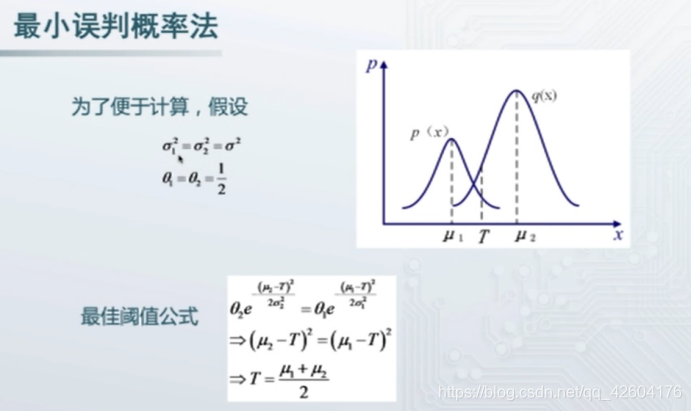
算法步驟：
分割前提基于全局的迭代算法
代碼實現：

void Iteration(Mat* srcImage, Mat* dstImage, float delta_T)
{//【1】求最大灰度和最小灰度byte max_his = 0;byte min_his = 255;int height = (*srcImage).rows;int width = (*srcImage).cols;for (int j = 0;j < height;j++){for (int i = 0;i < width;i++){if ((*srcImage).at<uchar>(j, i) > max_his){max_his = (*srcImage).at<uchar>(j, i);}if ((*srcImage).at<uchar>(j, i) < min_his){min_his = (*srcImage).at<uchar>(j, i);}}}float T = 0.5 * (max_his+ min_his);float m1 = 255;		//當m1 m2都取0時，會有錯誤float m2 = 0;float old_T = T;float new_T = 0.5 * (m1 + m2);int times = 10;//while (times--)while (abs(new_T - old_T) > delta_T){int G1 = 0;int G2 = 0;int timer_G1 = 0;int timer_G2 = 0;for (int j = 0;j < height;j++){for (int i = 0;i < width;i++){if ((*srcImage).at<uchar>(j, i) > old_T){G1 += (*srcImage).at<uchar>(j, i);timer_G1++;}else{G2 += (*srcImage).at<uchar>(j, i);timer_G2++;}}}m1 = G1 * 1.0f / timer_G1;m2 = G2 * 1.0f / timer_G2;old_T = new_T;new_T = 0.5 * (m1 + m2);}cout << "迭代方法閾值為：" << new_T << endl;	//根據得出的閾值二值化圖像for (int j = 0;j < height;j++){for (int i = 0;i < width;i++){if ((*srcImage).at<uchar>(j, i) > new_T){(*dstImage).at<uchar>(j, i) = 255;}else{(*dstImage).at<uchar>(j, i) = 0;}}}
}
int main()
{Mat srcImage = imread("D:\\opencv_picture_test\\新垣結衣\\test2.jpg", 0);	//讀入的時候轉化為灰度圖namedWindow("原始圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("原始圖", srcImage);Mat dstImage;dstImage.create(srcImage.rows, srcImage.cols, CV_8UC1);double time0 = static_cast<double>(getTickCount());	//記錄起始時間//閾值處理+二值化//My_P_tile(&srcImage,&dstImage,20);			//設P為20Iteration(&srcImage, &dstImage,0.02);//一系列處理之后time0 = ((double)getTickCount() - time0) / getTickFrequency();//cout << "此方法運行時間為：" << time0 << "秒" << endl;	//輸出運行時間namedWindow("效果圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("效果圖", dstImage);dstImage = My_Rraw_histogram(&srcImage);namedWindow("一維直方圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("一維直方圖", dstImage);waitKey(0);return 0;
}

當直方圖存在比較明顯的波谷時，這種方法是比較好的。δT控制迭代次數，下面是代碼實現效果
原圖
二值圖
一維直方圖
閾值

2基于Otsu最佳全局閾值方法（非常有效）

大津法又叫最大類間方差法、最大類間閾值法（OTSU）。
它的基本思想是，用一個閾值將圖像中的數據分為兩類，
一類中圖像的像素點的灰度均小于這個閾值，另一類中的圖像的像素點的灰度均大于或者等于該閾值。 //一般來說使用遍歷的方法來求
如果這兩個類中像素點的灰度的方差越大，說明獲取到的閾值就是最佳的閾值
（方差是灰度分布均勻性的一種度量,背景和前景之間的類間方差越大,說明構成圖像的兩部分的差別越大,當部分前景錯分為背景或部分背景錯分為前景都會導致兩部分差別變小。因此,使類間方差最大的分割意味著錯分概率最小。）。
則利用該閾值可以將圖像分為前景和背景兩個部分。
而我們所感興趣的部分一般為前景。
對于灰度分布直方圖有兩個峰值的圖像，大津法求得的Ｔ近似等于兩個峰值之間的低谷。
(這段闡述轉自這里https://www.jianshu.com/p/56b140f9535a)
公式推導
1
2
3
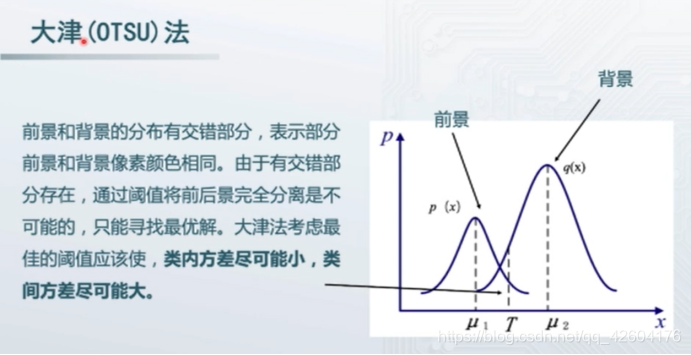
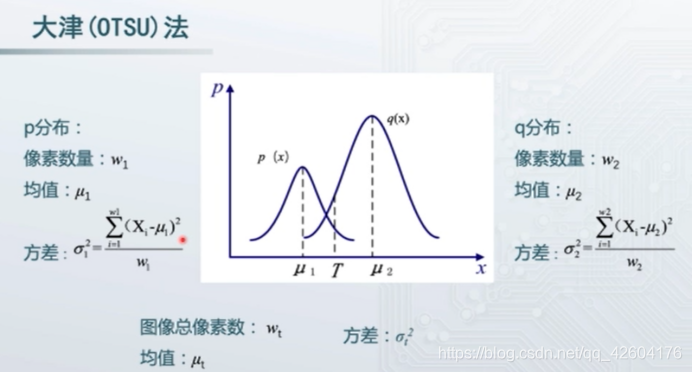
從一篇博客截來的圖，羅列了我們要計算的變量。https://blog.csdn.net/u012198575/article/details/81128799
需要計算的變量

代碼實現

void My_Ostu(Mat* srcImage, Mat* dstImage)
{int height = (*srcImage).rows;int width = (*srcImage).cols;int Ostu_Threshold = 0; //大津閾值int size = height * width;float variance;   //類間方差float maxVariance = 0, w1 = 0, w2 = 0, avgValue = 0;float u0 = 0, u1 = 0, u2 = 0;//生成灰度直方圖int pixels[256];float histgram[256];for (int i = 0; i < 256; i++){pixels[i] = 0;}for (int j = 0; j < height; j++){for (int i = 0; i < width; i++) {pixels[(*srcImage).at<uchar>(j, i)]++;}}for (int i = 0; i < 256; i++){histgram[i] = pixels[i] * 1.0f / size;}//遍歷找出類間方差最大（maxVariance）的閾值（Ostu_Threshold）for (int i = 0;i <= 255;i++){w1 = 0;w2 = 0;u1 = 0;u2 = 0;//計算背景像素占比,平均灰度for (int j = 0;j <= i;j++){w1 += histgram[j];u1 += histgram[j] * j;}u1 = u1 / w1;//計算前景像素占比,平均灰度w2 = 1 - w1;if (i == 255){u2 = 0;}else{for (int j = i + 1;j <= 255;j++){u2 += histgram[j] * j;}}u2 = u2 / w2;//計算類間方差variance = w1 * w2 * (u1 - u2) * (u1 - u2);if (variance > maxVariance){ //找到使灰度差最大的值maxVariance = variance;Ostu_Threshold = i;            //那個值就是閾值}}cout << "大津法閾值為：" << Ostu_Threshold << endl;//【3】二值化for (int j = 0; j < height; j++){for (int i = 0; i < width; i++){if ((*srcImage).at<uchar>(j, i) >= Ostu_Threshold){(*dstImage).at<uchar>(j, i) = 255;}else{(*dstImage).at<uchar>(j, i) = 0;}}}
}
int main()
{Mat srcImage = imread("D:\\opencv_picture_test\\新垣結衣\\test2.jpg", 0);	//讀入的時候轉化為灰度圖namedWindow("原始圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("原始圖", srcImage);Mat dstImage;dstImage.create(srcImage.rows, srcImage.cols, CV_8UC1);double time0 = static_cast<double>(getTickCount());	//記錄起始時間//閾值處理+二值化//My_P_tile(&srcImage,&dstImage,20);			//設P為20//My_Iteration(&srcImage, &dstImage,0.02);My_Ostu(&srcImage, &dstImage);//一系列處理之后time0 = ((double)getTickCount() - time0) / getTickFrequency();cout << "此方法運行時間為：" << time0 << "秒" << endl;	//輸出運行時間namedWindow("效果圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("效果圖", dstImage);dstImage = My_Rraw_histogram(&srcImage);namedWindow("一維直方圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("一維直方圖", dstImage);waitKey(0);return 0;
}

效果：
1
2

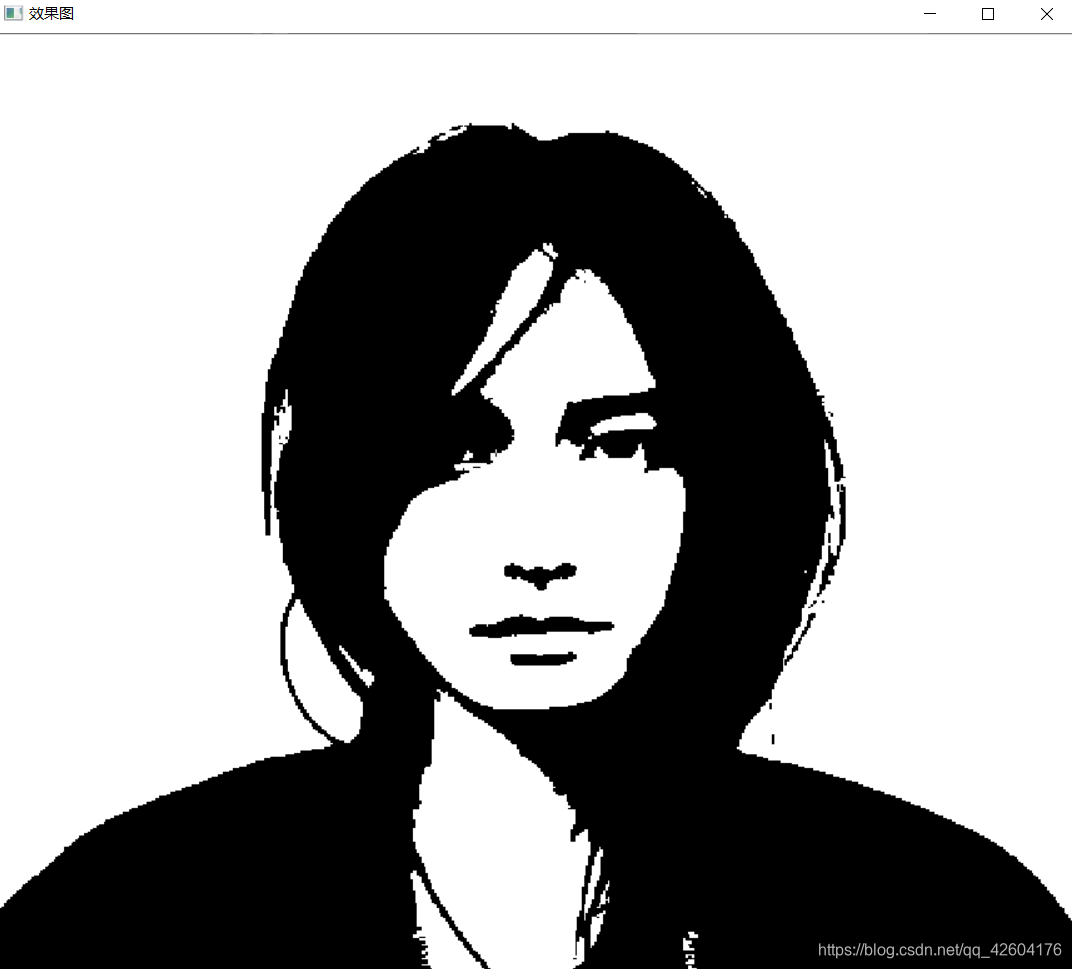
3用圖像平滑改善全局閾值處理

總的來說就是在二值化之前先用33或者55之類的均值模板將整個圖像處理一下。
不過這樣的壞處是使物體與背景的邊界變得有些模糊。侵蝕越多，邊界誤差越大。
在某些極端情況下，這種方法效果并不好。

4利用邊緣改進全局閾值處理

這種方法將關注聚焦于物體與背景的邊緣像素，在邊緣的灰度跳動非常明顯，由此得到的灰度直方圖將會得到很大的改善。
在這里我們求得邊緣的方法主要是梯度算子和拉普拉斯算子。
算法步驟：
算法步驟
一般來說我們確定閾值T是根據，梯度最大值或者拉普拉斯最大值的某百分比來確定的。當有不同需求時，采用不同的占比。

基于局部的閾值處理

這種閾值處理的目的是為了解決光照和反射帶來的問題。

1圖像分塊可變閾值處理

其實就是把一個圖片分割為多塊，分別使用大津閾值。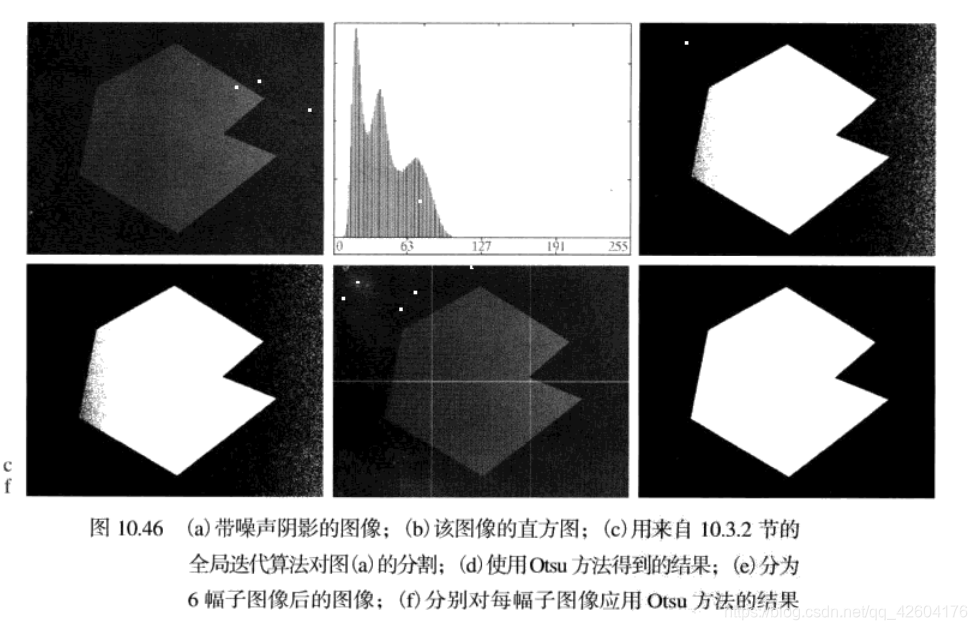分塊處理
分塊處理后的子圖像直方圖
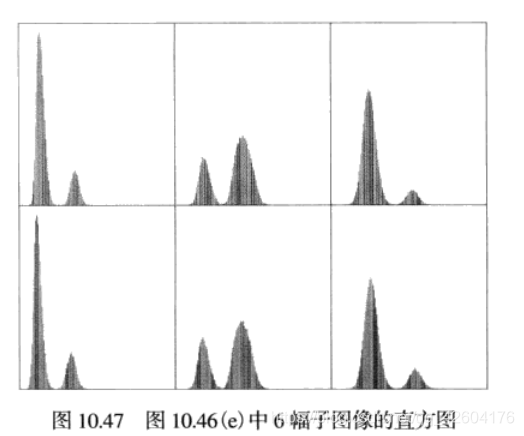
子圖像直方圖
上面的是書上的樣例，我把原圖截下來，試了試自己寫的代碼，效果并不是很好。
代碼實現：

void My_local_adaptive(Mat* srcImage, Mat* dstImage, int areas_of_H, int areas_of_W)		//局部自適應法   基于大津閾值areas_of_H：豎直方向分割的個數  areas_of_W：橫坐標方向分割的個數
{int height = (*srcImage).rows/ areas_of_H;			//每一小塊的heightint width = (*srcImage).cols/ areas_of_W;			//每一小塊的widthint Ostu_Threshold = 0; //大津閾值int size = height * width/ areas_of_H/ areas_of_W;		//每一小塊的size//一行一行地來for (int y = 0; y < areas_of_H; y++)	{for (int x = 0; x < areas_of_W; x++){float variance = 0;   //類間方差float maxVariance = 0, w1 = 0, w2 = 0, avgValue = 0;float u0 = 0, u1 = 0, u2 = 0;//生成areas_of_W*areas_of_H個局部灰度直方圖int pixels[256];float histgram[256];for (int i = 0; i < 256; i++){pixels[i] = 0;}//【處理每個小區域并且二值化】//【計算直方圖】for (int j = y* height; j < ((y + 1 == areas_of_H) ? (*srcImage).rows : (y + 1) * height); j++) //? : 是一個三目運算符，也是唯一的一個三目運算符。？前面表邏輯條件，：前面也就是？后面表示條件成立時的值，：后面表條件不成立時的值。例如，當a > b時，x = 1否則x = 0，可以寫成x = a > b ? 1 : 0。{for (int i = x * width; i < ((x + 1 == areas_of_W) ? (*srcImage).cols : (x + 1) * width); i++){pixels[(*srcImage).at<uchar>(j, i)]++;}}//【直方圖歸一化】for (int i = 0; i < 256; i++){histgram[i] = pixels[i] * 1.0f / size;}//遍歷找出類間方差最大（maxVariance）的閾值（Ostu_Threshold）for (int i = 0;i <= 255;i++){w1 = 0;w2 = 0;u1 = 0;u2 = 0;//計算背景像素占比,平均灰度for (int j = 0;j <= i;j++){w1 += histgram[j];u1 += histgram[j] * j;}u1=u1/w1;//計算前景像素占比,平均灰度w2 = 1 - w1;if (i == 255){u2 = 0;}else{for (int j = i + 1;j <= 255;j++){u2 += histgram[j] * j;}}u2=u2/w2;//計算類間方差variance = w1 * w2 * (u1 - u2) * (u1 - u2);if (variance > maxVariance){ //找到使灰度差最大的值maxVariance = variance;Ostu_Threshold = i;            //那個值就是閾值}}cout << "大津法閾值為：" << Ostu_Threshold << endl;//【3】二值化for (int j = y * height; j < ((y + 1 == areas_of_H) ? (*srcImage).rows : (y + 1) * height); j++) //? : 是一個三目運算符，也是唯一的一個三目運算符。？前面表邏輯條件，：前面也就是？后面表示條件成立時的值，：后面表條件不成立時的值。例如，當a > b時，x = 1否則x = 0，可以寫成x = a > b ? 1 : 0。{for (int i = x * width; i < ((x + 1 == areas_of_W) ? (*srcImage).cols : (x + 1) * width); i++){if ((*srcImage).at<uchar>(j, i) >= Ostu_Threshold){(*dstImage).at<uchar>(j, i) = 255;}else{(*dstImage).at<uchar>(j, i) = 0;}}}}}
}
int main()
{//Mat srcImage = imread("D:\\opencv_picture_test\\新垣結衣\\test2.jpg", 0);	//讀入的時候轉化為灰度圖//Mat srcImage = imread("D:\\opencv_picture_test\\miku\\miku2.jpg", 0);	//讀入的時候轉化為灰度圖Mat srcImage = imread("D:\\opencv_picture_test\\閾值處理\\帶噪聲陰影的圖.png", 0);	//讀入的時候轉化為灰度圖namedWindow("原始圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("原始圖", srcImage);Mat dstImage;dstImage.create(srcImage.rows, srcImage.cols, CV_8UC1);double time0 = static_cast<double>(getTickCount());	//記錄起始時間//閾值處理+二值化//My_P_tile(&srcImage,&dstImage,20);			//設P為20//My_Iteration(&srcImage, &dstImage,0.01);//My_Ostu(&srcImage, &dstImage);My_local_adaptive(&srcImage, &dstImage, 1, 2);//一系列處理之后time0 = ((double)getTickCount() - time0) / getTickFrequency();cout << "此方法運行時間為：" << time0 << "秒" << endl;	//輸出運行時間namedWindow("效果圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("效果圖", dstImage);dstImage = My_Rraw_histogram(&srcImage);namedWindow("一維直方圖", WINDOW_NORMAL);//WINDOW_NORMAL允許用戶自由伸縮窗口imshow("一維直方圖", dstImage);waitKey(0);return 0;
}

全局大津閾值效果
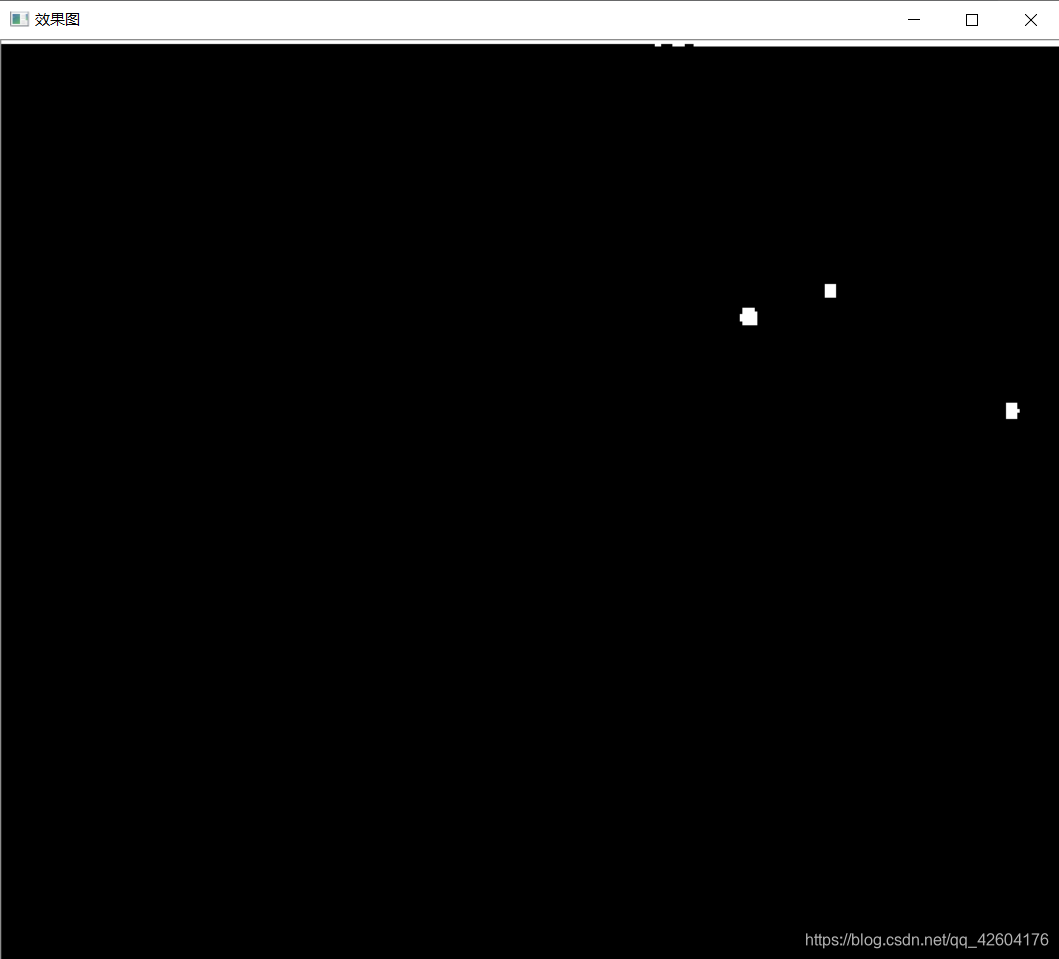
all black
2
局部閾值法：1*2分割
2
![2](https://img-blog.csdnimg.cn/202003
迭代閾值法：
1
2
看來仍然需要改進

2基于局部圖像特性的可變閾值處理

算法步驟：
1、計算以某一像素為中心的鄰域的灰度標準差和均值
計算所需變量
2、設定可變閾值算法步驟
3、觀察是否滿足閾值條件算法步驟
4、二值化
閾值處理

其中a和b都是需要人工整定。
效果圖：
效果圖

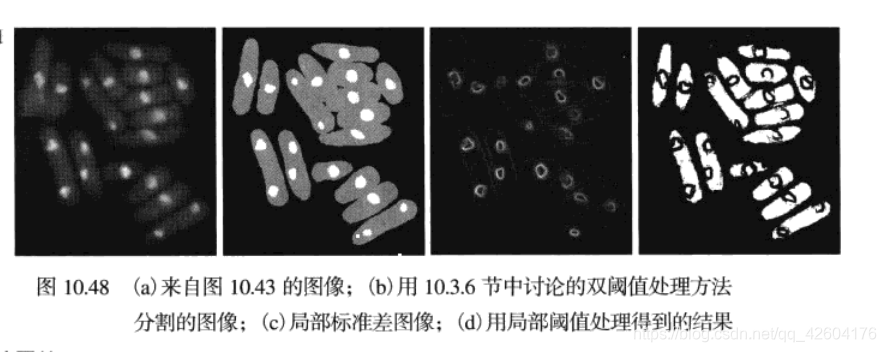
3基于移動平均法的可變閾值

算法描述
有關的鏈接：（這個算法我還沒有理解，等我理解了再來補充）
https://blog.csdn.net/qq_34510308/article/details/93162142

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/378771.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/378771.shtml
英文地址，請注明出處：http://en.pswp.cn/news/378771.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

java 用戶控件_C#自定義控件VS用戶控件

java 用戶控件_C#自定義控件VS用戶控件

C#中自定義控件VS用戶控件大比拼1 自定義控件與用戶控件區別WinForm中&#xff0c;用戶控件(User Control)&#xff1a;繼承自 UserControl&#xff0c;主要用于開發 Container 控件&#xff0c;Container控件可以添加其他Controls控件自定義控件(Custom Control)&#xff1a;繼…
閱讀更多...
Java FileDescriptor sync（）方法與示例

Java FileDescriptor sync（）方法與示例

FileDescriptor類sync()方法 (FileDescriptor Class sync() method) sync() method is available in java.io package. sync()方法在java.io包中可用。 sync() method is used to synchronize all the system buffer with the underlying device. sync()方法用于將所有系統緩沖…
閱讀更多...
windows 7資源管理器崩潰解決方法

windows 7資源管理器崩潰解決方法

最近被頻繁的資源管理器explorer崩潰搞得幾乎生活不能處理&#xff0c;一打開帶有視頻的文件夾&#xff0c;就explorer崩潰&#xff0c;要瘋了。 日志中含有mpc_mtcontrol.dll 查來查去&#xff0c;沒有一個確定的答案&#xff0c;baidu&#xff0c;google都沒用&#xff0c;最…
閱讀更多...
03-對圖像進行數值計算和加權融合

03-對圖像進行數值計算和加權融合

數值計算 import cv2img_1 cv2.imread(E:\Jupyter_workspace\study\data/beyond.png) img_2 cv2.imread(E:\Jupyter_workspace\study\data/water2.png)img_1_1 img_1 10 img_1[:2,:,0]#輸出前兩行就行 img_1_1[:2,:,0]#[h,w,c] img_2[:2,:,0]#[h,w,c](img_1 img_2)[:2,:,…
閱讀更多...
SQL Server存儲過程(procedure)應用

SQL Server存儲過程(procedure)應用

用戶反映&#xff0c;系統操作日志會使用數據庫快速增大&#xff0c;情況可參考下圖&#xff0c; 問題分析&#xff0c;整個系統每個頁面&#xff0c;都有寫記錄用戶操作代碼&#xff0c;修改或禁用這個代碼&#xff0c;看來是不可能的。 在原有系統參數表添加一個選項&#xf…
閱讀更多...
Opencv一維直方圖的繪制

Opencv一維直方圖的繪制

下面是我參考《opencv3編程入門》寫的繪制一維直方圖的代碼 using namespace cv; using namespace std; #define byte uchar #define TYEPE_GRAY 0 #define TYEPE_RGB 1 /*--------------------------繪制RGB三色一維直方圖-------------------------------------*/ Mat My_R…
閱讀更多...
Java類class forName（）方法及示例

Java類class forName（）方法及示例

類類forName()方法 (Class class forName() method) forName() method is available in java.lang package. forName()方法在java.lang包中可用。 forName() method is used to return the class object for the Class with the given class_name. forName()方法用于返回具有給…
閱讀更多...
04-圖像的閾值操作

04-圖像的閾值操作

對圖像的閾值操作 import cv2 import matplotlib.pyplot as pltimg cv2.imread(E:/Jupyter_workspace/study/data/cat.png,1) ret, thresh1 cv2.threshold(img,127,255,cv2.THRESH_BINARY) ret, thresh2 cv2.threshold(img,127,255,cv2.THRESH_BINARY_INV) ret, thresh3 c…
閱讀更多...
java虛擬機內存監控_深入理解JVM虛擬機9：JVM監控工具與診斷實踐

java虛擬機內存監控_深入理解JVM虛擬機9：JVM監控工具與診斷實踐

本文轉自&#xff1a;https://juejin.im/post/59e6c1f26fb9a0451c397a8c本系列文章將整理到我在GitHub上的《Java面試指南》倉庫&#xff0c;更多精彩內容請到我的倉庫里查看https://github.com/h3pl/Java-Tutorial喜歡的話麻煩點下Star哈文章將同步到我的個人博客&#xff1a;…
閱讀更多...
詳解:數據庫名、實例名、ORACLE_SID、數據庫域名、全局數據庫名、服務名

詳解:數據庫名、實例名、ORACLE_SID、數據庫域名、全局數據庫名、服務名

數據庫名、實例名、數據庫域名、全局數據庫名、服務名&#xff0c;這是幾個令很多初學者容易混淆的概念。相信很多初學者都與我一樣被標題上這些個概念搞得一頭霧水。我們現在就來把它們弄個明白。 一、數據庫名什么是數據庫名&#xff1f;數據庫名就是一個數據庫的標識&#…
閱讀更多...
顏色縮減 -利用指針、迭代器、動態地址實現訪問像素

顏色縮減 -利用指針、迭代器、動態地址實現訪問像素

為什么要使用顏色縮減 在對單通道圖像進行處理時&#xff0c;像素的可能值為256個&#xff0c;但處理多通道時&#xff0c;像素的處理就會相當麻煩&#xff0c;其實用這些顏色中具有代表性的一小部分就可以達到同樣的效果&#xff0c;所以顏色空間縮減就可以派上用場了。一個信…
閱讀更多...
setlenient_Java日歷setLenient（）方法與示例

setlenient_Java日歷setLenient（）方法與示例

setlenient日歷類setLenient()方法 (Calendar Class setLenient() method) setLenient() method is available in java.util package. setLenient()方法在java.util包中可用。 setLenient() method is used to set or unset lenient status of date or time interpretations. s…
閱讀更多...
PowerShell_9_零基礎自學課程_9_高級主題：靜態類和類的操作

PowerShell_9_零基礎自學課程_9_高級主題：靜態類和類的操作

哈哈&#xff0c;昨天弄了個ubuntu 11.10在虛擬機上運行&#xff0c;發現11.10界面非常絢麗&#xff0c;但是其需要的系統資源非常多&#xff0c;我虛擬機設定內存為512M&#xff0c;1個CPU4個核心&#xff0c; 進入以后發現根本動不了&#xff0c;因此今天我就下載了一個Fedor…
閱讀更多...
05-圖像的平滑處理（不同的濾波操作）

05-圖像的平滑處理（不同的濾波操作）

對圖像進行平滑處理實則就是對圖像進行濾波操作罷了 每張圖片都有若干個像素點所構成&#xff0c;濾波操作上就是將照片上的某些部分像素點進行修改從而達到平滑的效果 先展示一下原圖 import cv2 img cv2.imread(E:\Jupyter_workspace\study\data/test1.png)cv2.imshow(te…
閱讀更多...
js刪除mysql記錄_（DELETEUPDATE）修改、刪除數據記錄_MySQL

js刪除mysql記錄_（DELETEUPDATE）修改、刪除數據記錄_MySQL

有時&#xff0c;希望除去某些記錄或更改它們的內容。DELETE 和 UPDATE 語句令我們能做到這一點。用update修改記錄UPDATE tbl_name SET 要更改的列WHERE 要更新的記錄這里的 WHERE 子句是可選的&#xff0c;因此如果不指定的話&#xff0c;表中的每個記錄都被更新。例如&#…
閱讀更多...
C++設計模式之Abstract Factory模式

C++設計模式之Abstract Factory模式

一、功能 　　提供一個創建一系列相關或相互依賴對象的接口&#xff0c;而無需指定它們具體的類。 二、結構圖類廠最基本的結構示意圖如下&#xff1a; 在實際應用中&#xff0c;類廠模式可以擴充到很復雜的情況&#xff0c;如下圖所示&#xff1a; 三、優缺點 優點&#xff1…
閱讀更多...
數字圖像處理小練習存檔1

數字圖像處理小練習存檔1

小練習的題目&#xff1a; 1、讀取一張圖&#xff0c;分解RGB三個通道 /************練習1**********************/ int main() {Mat img1 imread("D:\\opencv_picture_test\\miku2.jpg",2|4); //灰度圖if (img1.empty()){printf("Could not find the imag…
閱讀更多...
UIImage 壓縮

UIImage 壓縮

1.改變圖片大小 -(UIImage*)imageWithImage:(UIImage*)image scaledToSize:(CGSize)newSize {// Create a graphics image contextUIGraphicsBeginImageContext(newSize);// Tell the old image to draw in this new context, with the desired// new size[image drawInRect:CG…
閱讀更多...
06-對圖像進行腐蝕操作

06-對圖像進行腐蝕操作

形態學中的腐蝕操作一般處理的圖像數據為二值的 cv2.erode(img,kernel,iterations 1) kernel表示拿多大的卷積核去腐蝕 iterations表示迭代次數 可以將一些帶有毛毛的圖像去毛毛化 原圖 import cv2 import numpy as npdef show_photo(name,picture):cv2.imshow(name,picture)…
閱讀更多...
Java BufferedReader skip（）方法與示例

Java BufferedReader skip（）方法與示例

BufferedReader類skip()方法 (BufferedReader Class skip() method) skip() method is available in java.io package. skip()方法在java.io包中可用。 skip() method is used to skip the given number of bytes of characters (n_bytes_of_char) from this BufferedReader. s…
閱讀更多...
最新文章

Copyright @ 2022~2023