目錄
- 【1】解析法實現一元線性回歸
- python列表實現
- 利用Numpy實現
- 利用TensorFlow實現
- 數據和模型可視化
- 【2】解析法實現多元線性回歸
- 利用Numpy實現
- 需要用到的NumPy數組運算函數
- 數據和模型可視化
- 繪制空間點集:
- 繪制空間平面圖:
- 繪制線框圖并且與散點圖對比:
【1】解析法實現一元線性回歸
公式:
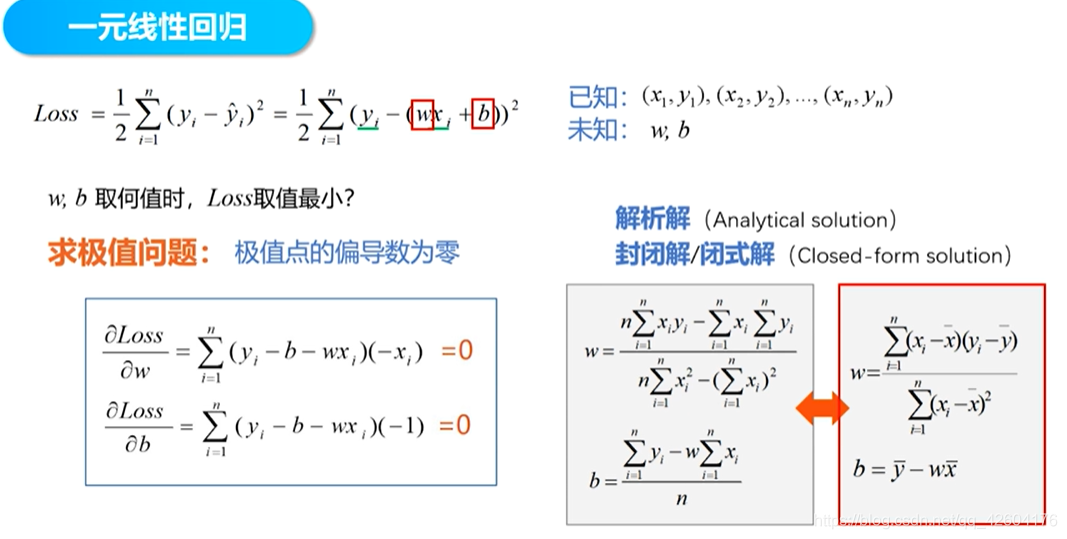
代碼:
python列表實現
#加載樣本數據
x=[137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21]
y=[145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30]
meanX=sum(x)/len(x)
meanY=sum(y)/len(y)
sumXY=0.0
sumX=0.0
for i in range(len(x)):sumXY+=(x[i]-meanX)*(y[i]-meanY)sumX+=(x[i]-meanX)*(x[i]-meanX)
w=sumXY/sumX
b=meanY-w*meanX
print("w=",w)
print("b=",b)
x_test=[128.15,45.00,141.43,106.27,99.00,53.84,85.36,70.00]
print("面積\t估計房價")
for i in range(len(x_test)):print(x_test[i],"\t",round(w*x_test[i]+b,2))
結果:
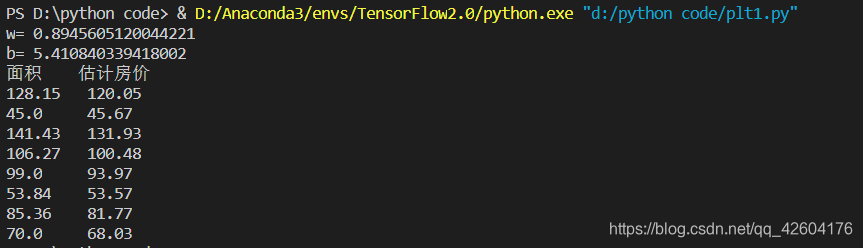
利用Numpy實現
import numpy as np
x=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
meanX=np.mean(x)
meanY=np.mean(y)
sumXY=np.sum((x-meanX)*(y-meanY))
sumX=np.sum((x-meanX)*(x-meanX))
w=sumXY/sumX
b=meanY-w*meanX
print("w=",w)
print("b=",b)
x_test=np.array([128.15,45.00,141.43,106.27,99.00,53.84,85.36,70.00])
y_pred = w*x_test+b
print("面積\t估計房價")
for i in range(y_pred.size):print(x_test[i],"\t",np.round(y_pred[i],2))
利用TensorFlow實現
import tensorflow as tf
x=tf.constant([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y=tf.constant([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
meanX=tf.reduce_mean(x)
meanY=tf.reduce_mean(y)
sumXY=tf.reduce_sum((x-meanX)*(y-meanY))
sumX=tf.reduce_sum((x-meanX)*(x-meanX))
w=sumXY/sumX
b=meanY-w*meanX
print("w=",w)
print("b=",b)
x_test=tf.constant([128.15,45.00,141.43,106.27,99.00,53.84,85.36,70.00])
y_pred = w*x_test+b
print(y_pred)
數據和模型可視化
#解析法實現一元線性回歸
# #Realization of one variable linear regression by analytic method
#導入庫
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#設置字體
plt.rcParams['font.sans-serif'] =['SimHei']
#加載樣本數據
x=tf.constant([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
y=tf.constant([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
#學習模型-計算w,b
meanX=tf.reduce_mean(x)
meanY=tf.reduce_mean(y)
sumXY=tf.reduce_sum((x-meanX)*(y-meanY))
sumX=tf.reduce_sum((x-meanX)*(x-meanX))
w=sumXY/sumX
b=meanY-w*meanX
print("權值w=",w.numpy())
print("偏置b=",b.numpy())
print("線性模型:y=",w.numpy(),"*x+",b.numpy())
#預測房價
x_test=np.array([128.15,45.00,141.43,106.27,99.00,53.84,85.36,70.00])
y_pred = (w*x_test+b).numpy()#將張量類型轉化為numpy數組類型
print("面積\t估計房價")
n=len(x_test)
for i in range(n):print(x_test[i],"\t",round(y_pred[i],2))
#模型和數據可視化
plt.figure()
#繪制散點圖
#張量和數組都可以作為散點函數的輸入提供點坐標
plt.scatter(x,y,color="red",label="銷售記錄")
plt.scatter(x_test,y_pred,color="blue",label="預測房價")
plt.plot(x_test,y_pred,color="green",label="擬合直線",linewidth=2)
#設置坐標軸的標簽文字和字號
plt.xlabel("面積(平方米)",fontsize=14)
plt.xlabel("價格(萬元)",fontsize=14)
#設置坐標軸的范圍
plt.xlim((40,150))
plt.ylim((40,150))
#設置標題文字和字號
plt.suptitle("商品房銷售價格評估系統v1.0",fontsize=20)
#在左上方顯示圖例
plt.legend(loc="upper left")
#顯示整個繪圖
plt.show()
結果:
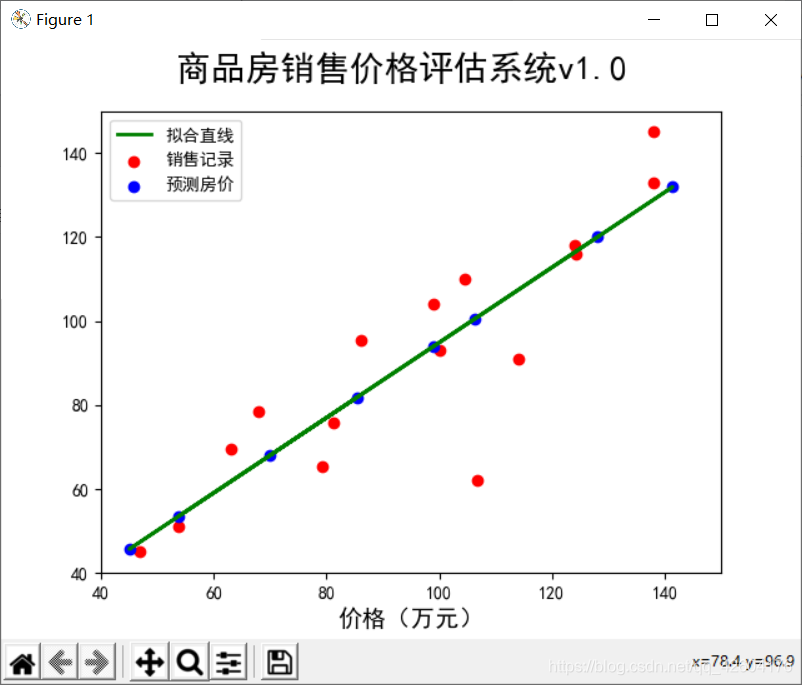 | 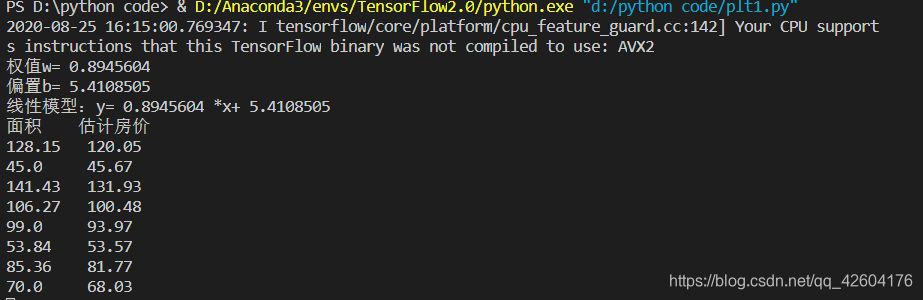 |
【2】解析法實現多元線性回歸
利用Numpy實現
需要用到的NumPy數組運算函數
| 功能 | 函數 |
|---|---|
| 數組堆疊 | np.stack( ) |
| 改變數組形狀 | np.reshape( ) |
| 矩陣相乘 | np.matmul( ) |
| 矩陣轉置 | np.transpose( ) |
| 矩陣求逆 | np.linalg.inv( ) |
公式:

代碼:
#解析法實現多元線性回歸
#Realization of multiple linear regression by analytic method
#導入庫
import numpy as np
#=======================【1】加載樣本數據===============================================
x1=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
x2=np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
#=======================【2】數據處理===============================================
x0=np.ones(len(x1))
#堆疊屬性數組,構造屬性矩陣
#從(16,)到(16,3),因為新出現的軸是第二個軸所以axis為1
X=np.stack((x0,x1,x2),axis=1)
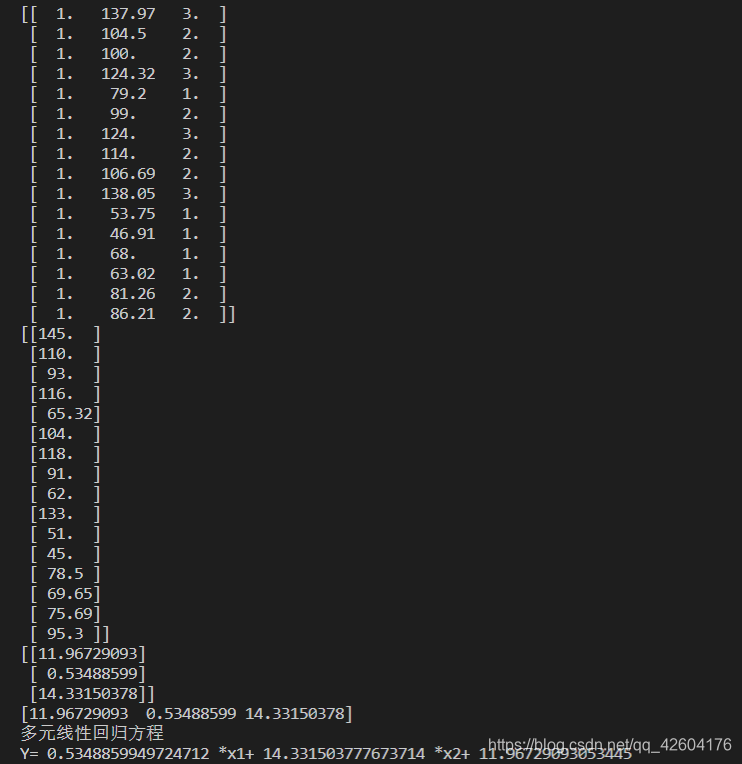
print(X)
#得到形狀為一列的數組
Y=np.array(y).reshape(-1,1)
print(Y)
#=======================【3】求解模型參數===============================================
Xt=np.transpose(X) #計算X'
XtX_1=np.linalg.inv(np.matmul(Xt,X)) #計算(X'X)-1
XtX_1_Xt=np.matmul(XtX_1,Xt) #計算(X'X)-1X'
W=np.matmul(XtX_1_Xt,Y) #W=((X'X)-1)X'Y
print(W)
W=W.reshape(-1)
print(W)
print("多元線性回歸方程")
print("Y=",W[1],"*x1+",W[2],"*x2+",W[0])
#=======================【4】預測房價===============================================
print("請輸入房屋面積和房間數,預測房屋銷售價格")
x1_test=float(input("商品房面積:"))
x2_test=int(input("房間數:"))
y_pred=W[1]*x1_test+W[2]*x2_test+W[0]
print("預測價格:",round(y_pred,2),"萬元")
效果:
 |  |  |
數據和模型可視化
繪制空間點集:
#解析法實現多元線性回歸
#Realization of multiple linear regression by analytic method
#導入庫與模塊
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#=======================【1】加載樣本數據===============================================
x1=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
x2=np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
#=======================【2】數據處理===============================================
x0=np.ones(len(x1))
#堆疊屬性數組,構造屬性矩陣
#從(16,)到(16,3),因為新出現的軸是第二個軸所以axis為1
X=np.stack((x0,x1,x2),axis=1)
print(X)
#得到形狀為一列的數組
Y=np.array(y).reshape(-1,1)
print(Y)
#=======================【3】求解模型參數===============================================
Xt=np.transpose(X) #計算X'
XtX_1=np.linalg.inv(np.matmul(Xt,X)) #計算(X'X)-1
XtX_1_Xt=np.matmul(XtX_1,Xt) #計算(X'X)-1X'
W=np.matmul(XtX_1_Xt,Y) #W=((X'X)-1)X'Y
print(W)
W=W.reshape(-1)
print(W)
print("多元線性回歸方程")
print("Y=",W[1],"*x1+",W[2],"*x2+",W[0])
#模型和數據可視化
fig=plt.figure(figsize=(8,6))
#創建3D繪圖對象
ax3d=Axes3D(fig)
#用來改變視角的函數
#elev:視角的水平高度 水平旋轉的角度
#ax3d.view_init(elev=0,azim=-90)
#繪制散點圖
#張量和數組都可以作為散點函數的輸入提供點坐標
ax3d.scatter(x1,x2,y,color="b",marker="*")
ax3d.set_xlabel('Area',color='r',fontsize=16)
ax3d.set_ylabel('Room',color='r',fontsize=16)
ax3d.set_zlabel('Price',color='r',fontsize=16)
#設置y軸坐標值刻度
ax3d.set_yticks([1,2,3])
ax3d.set_zlim3d(30,160)
plt.show()
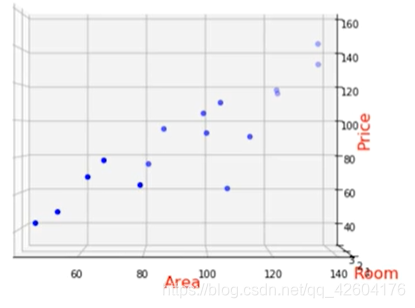 ax3d.view_init(elev=0,azim=-90) ax3d.view_init(elev=0,azim=-90) | 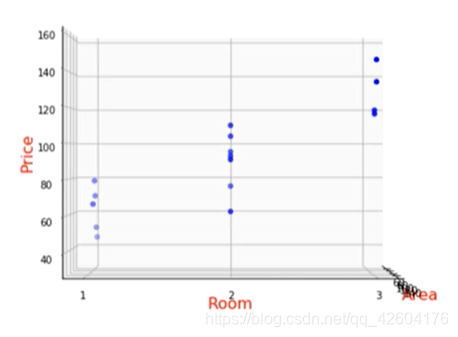 ax3d.view_init(elev=0,azim=0) ax3d.view_init(elev=0,azim=0) |
繪制空間平面圖:
#解析法實現多元線性回歸
#Realization of multiple linear regression by analytic method
#導入庫與模塊
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#=======================【1】加載樣本數據===============================================
x1=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
x2=np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
#=======================【2】數據處理===============================================
x0=np.ones(len(x1))
#堆疊屬性數組,構造屬性矩陣
#從(16,)到(16,3),因為新出現的軸是第二個軸所以axis為1
X=np.stack((x0,x1,x2),axis=1)
print(X)
#得到形狀為一列的數組
Y=np.array(y).reshape(-1,1)
print(Y)
#=======================【3】求解模型參數===============================================
Xt=np.transpose(X) #計算X'
XtX_1=np.linalg.inv(np.matmul(Xt,X)) #計算(X'X)-1
XtX_1_Xt=np.matmul(XtX_1,Xt) #計算(X'X)-1X'
W=np.matmul(XtX_1_Xt,Y) #W=((X'X)-1)X'Y
print(W)
W=W.reshape(-1)
print(W)
print("多元線性回歸方程")
print("Y=",W[1],"*x1+",W[2],"*x2+",W[0])
#模型和數據可視化
X1,X2=np.meshgrid(x1,x2)
#平面方程
Y_PRED=W[0]+W[1]*X1+W[2]*X2
#創建3D繪圖對象
fig=plt.figure()
ax3d=Axes3D(fig)
#繪制空間平面圖
ax3d.plot_surface(X1,X2,Y_PRED,cmap="coolwarm")
ax3d.set_xlabel('Area',color='r',fontsize=14)
ax3d.set_ylabel('Room',color='r',fontsize=14)
ax3d.set_zlabel('Price',color='r',fontsize=14)
ax3d.set_yticks([1,2,3])
plt.show()
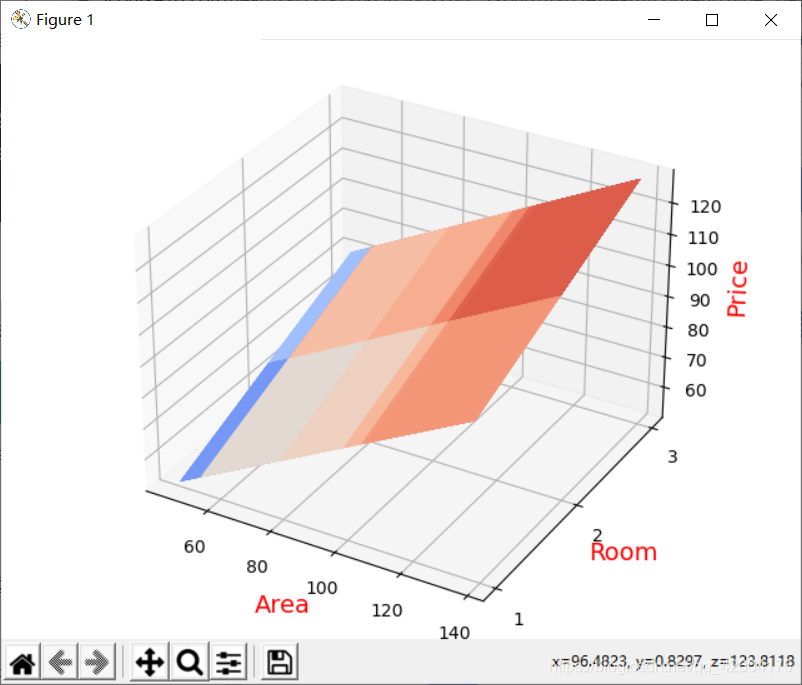
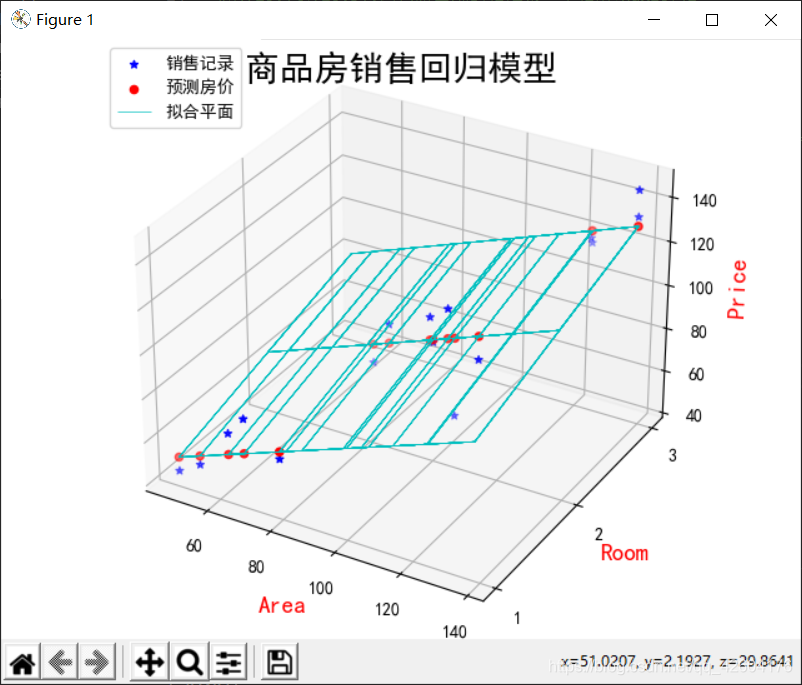
繪制線框圖并且與散點圖對比:
#解析法實現多元線性回歸
#Realization of multiple linear regression by analytic method
#導入庫與模塊
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#=======================【1】加載樣本數據===============================================
x1=np.array([137.97,104.50,100.00,124.32,79.20,99.00,124.00,114.00,106.69,138.05,53.75,46.91,68.00,63.02,81.26,86.21])
x2=np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])
y=np.array([145.00,110.00,93.00,116.00,65.32,104.00,118.00,91.00,62.00,133.00,51.00,45.00,78.50,69.65,75.69,95.30])
#=======================【2】數據處理===============================================
x0=np.ones(len(x1))
#堆疊屬性數組,構造屬性矩陣
#從(16,)到(16,3),因為新出現的軸是第二個軸所以axis為1
X=np.stack((x0,x1,x2),axis=1)
print(X)
#得到形狀為一列的數組
Y=np.array(y).reshape(-1,1)
print(Y)
#=======================【3】求解模型參數===============================================
Xt=np.transpose(X) #計算X'
XtX_1=np.linalg.inv(np.matmul(Xt,X)) #計算(X'X)-1
XtX_1_Xt=np.matmul(XtX_1,Xt) #計算(X'X)-1X'
W=np.matmul(XtX_1_Xt,Y) #W=((X'X)-1)X'Y
print(W)
W=W.reshape(-1)
print(W)
print("多元線性回歸方程")
print("Y=",W[1],"*x1+",W[2],"*x2+",W[0])
y_pred=W[0]+W[1]*x1+W[2]*x2
#設置字體
plt.rcParams['font.sans-serif'] =['SimHei']
#模型和數據可視化
X1,X2=np.meshgrid(x1,x2)
#平面方程
Y_PRED=W[0]+W[1]*X1+W[2]*X2
#創建3D繪圖對象
fig=plt.figure()
ax3d=Axes3D(fig)
#繪制散點圖與線框圖
ax3d.scatter(x1,x2,y,color='b',marker="*",label="銷售記錄")
ax3d.scatter(x1,x2,y_pred,color='r',label="預測房價")
ax3d.plot_wireframe(X1,X2,Y_PRED,color='c',linewidth=0.5,label="擬合平面")ax3d.set_xlabel('Area',color='r',fontsize=14)
ax3d.set_ylabel('Room',color='r',fontsize=14)
ax3d.set_zlabel('Price',color='r',fontsize=14)
ax3d.set_yticks([1,2,3])
plt.suptitle("商品房銷售回歸模型",fontsize=20)
plt.legend(loc="upper left")
plt.show()
方法)



)


方法)



——系統調用和參數傳遞)
)
方法與示例)


以及NCC的思考整理)

方法與示例)
