一、張量

張量表示由一個數值組成的數組，這個數組可能有多個維度

import torch

x = torch.arange(15)
x # tensor([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])

1，shape

shape屬性可以訪問張量的形狀

x.shape # torch.Size([15])

2，numel()

numel()函數可以訪問張量中元素的總數

x.numel() # 15

3，reshape()

可以調用reshape()函數，改變一個張量的形狀而不改變元素數量和元素值

x = x.reshape(3,5)
x
"""
tensor([[ 0,  1,  2,  3,  4],[ 5,  6,  7,  8,  9],[10, 11, 12, 13, 14]])
"""

4，使用全0、全1、其他常量或者從特定分布中隨機采樣的數字

torch.zeros((2, 3, 4))
"""
tensor([[[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]],[[0., 0., 0., 0.],[0., 0., 0., 0.],[0., 0., 0., 0.]]])
"""

torch.ones((2, 3, 4))
"""
tensor([[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]],[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]]])
"""

torch.ones((3,4,5))*8
"""
tensor([[[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.]],[[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.]],[[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.],[8., 8., 8., 8., 8.]]])
"""

torch.randn(3, 4)
"""
tensor([[-2.9078,  0.4283, -0.7296,  0.0575],[-1.3947,  0.5494,  0.9782, -0.3510],[-0.2191, -3.2434, -1.6111,  2.0091]])
"""

5，為所需張量中的每個元素賦予確定值

通過提供包含數值的 Python 列表（或嵌套列表）來為所需張量中的每個元素賦予確定值

torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
"""
tensor([[2, 1, 4, 3],[1, 2, 3, 4],[4, 3, 2, 1]])
"""

6，標準算術運算

+、-、*、/、**、^

a1 = torch.tensor([1,2,4,8],dtype=torch.float32)
a2 = torch.tensor([2,2,2,2])
a1 + a2, a1 - a2, a1 * a2, a1 / a2, a1 ** a2 , torch.exp(a2)
"""
(tensor([ 3.,  4.,  6., 10.]),tensor([-1.,  0.,  2.,  6.]),tensor([ 2.,  4.,  8., 16.]),tensor([0.5000, 1.0000, 2.0000, 4.0000]),tensor([ 1.,  4., 16., 64.]),tensor([7.3891, 7.3891, 7.3891, 7.3891]))"""

7，cat()

可以調用cat()函數，把多個張量連結(concatenate)在一起
dim=0張量列連接
dim=1張量行連接

X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X, Y, torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)
"""
(tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.]]),tensor([[2., 1., 4., 3.],[1., 2., 3., 4.],[4., 3., 2., 1.]]),tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[ 2.,  1.,  4.,  3.],[ 1.,  2.,  3.,  4.],[ 4.,  3.,  2.,  1.]]),tensor([[ 0.,  1.,  2.,  3.,  2.,  1.,  4.,  3.],[ 4.,  5.,  6.,  7.,  1.,  2.,  3.,  4.],[ 8.,  9., 10., 11.,  4.,  3.,  2.,  1.]]))
"""

8，sum()

對張量中的所有元素進行求和，產生一個只有一個元素的張量

X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
X, X.sum()
"""
(tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.]]),tensor(66.))
"""

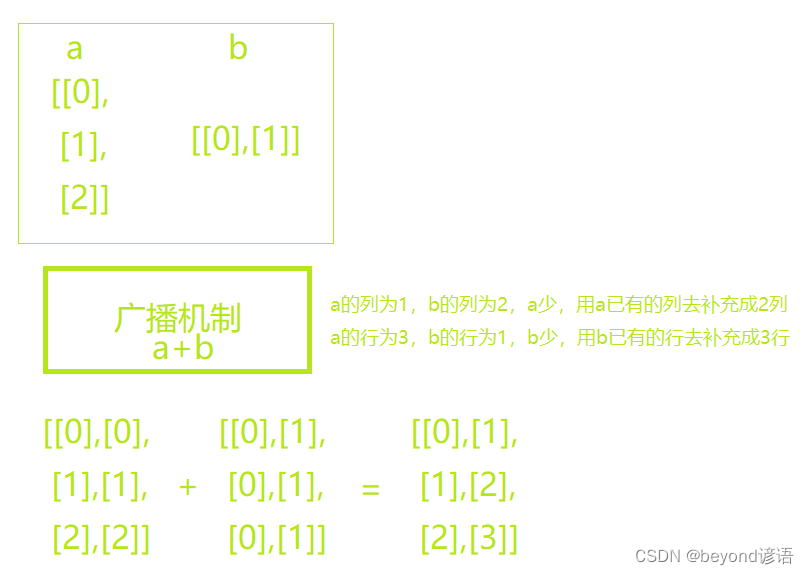
9，廣播機制

即使形狀不同，仍然可以通過調用廣播機制(broadcasting mechanism)來執行按元素操作
例如：a和b形狀不同，相加不報錯，為啥捏？系統會通過廣播機制將a和b自動擴充，進行相加

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a, b, a + b
"""
(tensor([[0],[1],[2]]),tensor([[0, 1]]),tensor([[0, 1],[1, 2],[2, 3]]))
"""

在這里插入圖片描述

10，內存分配

Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(id(Y))
Y = Y + X
print(id(Y))
"""
1426209183608
1426209185448
"""

Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
Z = torch.zeros_like(Y)
print(id(Z))
Z = X + Y
print(id(Z))
"""
1426207453976
1426198282056
"""

如果在后續計算中沒有重復使用 X，可以使用 X[:] = X + Y 或 X += Y 來減少操作的內存開銷

Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(id(Y))
Y += X
print(id(Y))
"""
1426209185608
1426209185608
"""

Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
Z = torch.zeros_like(Y)
print(id(Z))
Z[:] = X + Y
print(id(Z))
"""
1426198282056
1426198282056
"""

11，NumPy張量

X = torch.arange(12, dtype=torch.float32).reshape((3, 4))
A = X.numpy()
B = torch.tensor(A)
type(X), type(A), type(B)
"""
(torch.Tensor, numpy.ndarray, torch.Tensor)
"""

12，Python 標量

a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
"""
(tensor([3.5000]), 3.5, 3.5, 3)
"""

二、數據預處理

1，創建數據集

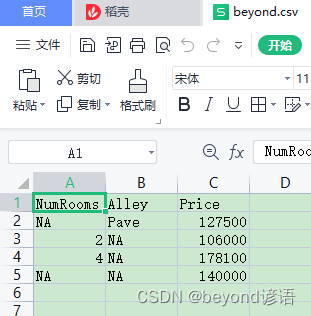
首先創建一個人工數據集，并存儲在CSV（逗號分隔值）文件 ../data/beyond.csv中

import osos.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:f.write('NumRooms,Alley,Price\n')  # 列名f.write('NA,Pave,127500\n')  # 每行表示一個數據樣本f.write('2,NA,106000\n')f.write('4,NA,178100\n')f.write('NA,NA,140000\n')

在這里插入圖片描述
房間數量（“NumRooms”）、巷子類型（“Alley”）、房屋價格（“Price”）

2，加載原始數據集

導入pandas包并調用read_csv函數
“NaN”項代表缺失值

import pandas as pddata = pd.read_csv(data_file)
print(data)
"""NumRooms Alley   Price
0       NaN  Pave  127500
1       2.0   NaN  106000
2       4.0   NaN  178100
3       NaN   NaN  140000
"""

3，處理缺失值

為了處理缺失的數據，典型的方法包括插值法和刪除法
插值法用一個替代值彌補缺失值
刪除法則直接忽略缺失值

在這里，考慮插值法
通過位置索引iloc，將data分成inputs和outputs，其中前者為data的前兩列，而后者為data的最后一列

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
inputs, outputs
"""
(   NumRooms Alley0       NaN  Pave1       2.0   NaN2       4.0   NaN3       NaN   NaN,0    1275001    1060002    1781003    140000Name: Price, dtype: int64)
"""

對于inputs中缺少的數值，用同一列的均值替換“NaN”項

inputs = inputs.fillna(inputs.mean())
print(inputs)
"""NumRooms Alley
0       3.0  Pave
1       2.0   NaN
2       4.0   NaN
3       3.0   NaN
"""

對于inputs中的類別值或離散值，將“NaN”視為一個類別。
由于“巷子類型”（“Alley”）列只接受兩種類型的類別值“Pave”和“NaN”， pandas可以自動將此列轉換為兩列“Alley_Pave”和“Alley_nan”。
巷子類型為“Pave”的行會將“Alley_Pave”的值設置為1，“Alley_nan”的值設置為0。
缺少巷子類型的行會將“Alley_Pave”和“Alley_nan”分別設置為0和1。

inputs = pd.get_dummies(inputs, dummy_na=True)
print(inputs)
"""NumRooms  Alley_Pave  Alley_nan
0       3.0           1          0
1       2.0           0          1
2       4.0           0          1
3       3.0           0          1
"""

4，轉換為張量格式

import torchx, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
x, y
"""
(tensor([[3., 1., 0.],[2., 0., 1.],[4., 0., 1.],[3., 0., 1.]], dtype=torch.float64),tensor([127500, 106000, 178100, 140000]))
"""

三、線性代數

1，標量

標量由只有一個元素的張量表示

from mxnet import np, npx
import torchnpx.set_np()x = np.array(3.0)
y = np.array(2.0)x + y, x * y, x / y, x ** y
"""
(array(5.), array(6.), array(1.5), array(9.))
"""

2，向量

可以將向量視為標量值組成的列表，這些標量值稱為向量的元素（element）或分量（component）

通過一維張量處理向量

x = torch.arange(4)
x
"""
x = torch.arange(4)
x
1
x = torch.arange(4)
2
x
tensor([0, 1, 2, 3])
"""

使用下標來引用向量的任一元素

x[2]
"""
tensor(2)
"""

2.1，len()

通過調用Python的內置len()函數來訪問張量的長度

len(x)
"""
4
"""

2.2，shape

當用張量表示一個向量（只有一個軸）時，可以通過.shape屬性訪問向量的長度
形狀（shape）是一個元素組，列出了張量沿每個軸的長度（維數）
對于只有一個軸的張量，形狀只有一個元素。

x.shape
"""
torch.Size([4])
"""

向量或軸的維度被用來表示向量或軸的長度，即向量或軸的元素數量。
然而，張量的維度用來表示張量具有的軸數。
在這個意義上，張量的某個軸的維數就是這個軸的長度。

3，矩陣

矩陣，在代碼中表示為具有兩個軸的張量。

指定兩個分量和來創建一個形狀為m×n的矩陣

A = torch.arange(20).reshape(5, 4)
A
"""
tensor([[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11],[12, 13, 14, 15],[16, 17, 18, 19]])
"""

矩陣的轉置T

A.T
"""
tensor([[ 0,  4,  8, 12, 16],[ 1,  5,  9, 13, 17],[ 2,  6, 10, 14, 18],[ 3,  7, 11, 15, 19]])
"""

4，張量

向量是標量的推廣，矩陣是向量的推廣
向量是一階張量，矩陣是二階張量
張量用特殊字體的大寫字母表示(例如：X、Y、Z)

X = torch.arange(24).reshape(2, 3, 4)
X
"""
tensor([[[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]],[[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]]])
"""

5，張量算法的基本性質

將兩個相同形狀的矩陣相加，會在這兩個矩陣上執行元素加法

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通過分配新內存，將A的一個副本分配給B
A, A + B
"""
(tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),tensor([[ 0.,  2.,  4.,  6.],[ 8., 10., 12., 14.],[16., 18., 20., 22.],[24., 26., 28., 30.],[32., 34., 36., 38.]]))
"""

兩個矩陣的按元素乘法稱為Hadamard積（Hadamard product）
即，對應元素相乘

A * B
"""
tensor([[  0.,   1.,   4.,   9.],[ 16.,  25.,  36.,  49.],[ 64.,  81., 100., 121.],[144., 169., 196., 225.],[256., 289., 324., 361.]])
"""

將張量乘以或加上一個標量不會改變張量的形狀，其中張量的每個元素都將與標量相加或相乘。

a = 2
X = torch.arange(24).reshape(2, 3, 4)
X, a + X, (a * X).shape
"""
(tensor([[[ 0,  1,  2,  3],[ 4,  5,  6,  7],[ 8,  9, 10, 11]],[[12, 13, 14, 15],[16, 17, 18, 19],[20, 21, 22, 23]]]),tensor([[[ 2,  3,  4,  5],[ 6,  7,  8,  9],[10, 11, 12, 13]],[[14, 15, 16, 17],[18, 19, 20, 21],[22, 23, 24, 25]]]),torch.Size([2, 3, 4]))"""

6，降維

6.1，sum()

計算任意張量元素的和

x = torch.arange(5, dtype=torch.float32)
x, x.sum()
"""
(tensor([0., 1., 2., 3., 4.]), tensor(10.))
"""

也可以表示任意形狀張量的元素和

A = torch.arange(6).reshape(2, 3)
A, A.shape, A.sum()
"""
(tensor([[0, 1, 2],[3, 4, 5]]),torch.Size([2, 3]),tensor(15))
"""

默認情況下，調用求和函數會沿所有的軸降低張量的維度，使它變為一個標量
也可以指定張量沿哪一個軸來通過求和降低維度
axis=0，同一列所在的所有行元素相加
axis=1，同一行所在的所有列元素相加

A_sum_axis0 = A.sum(axis)#同一列所在的所有行元素相加
A_sum_axis0, A_sum_axis0.shape
"""
(tensor([3, 5, 7]), torch.Size([3]))
"""

指定axis=1將通過匯總所有列的元素降維（軸1）
因此，輸入軸1的維數在輸出形狀中消失

A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
"""
(tensor([ 3, 12]), torch.Size([2]))
"""

沿著行和列對矩陣求和，等價于對矩陣的所有元素進行求和

A.sum(axis=[0, 1]), A.sum()
"""
(tensor(15), tensor(15))
"""

6.2，mean()

總和除以元素總數來計算平均值
也可以調用函數來計算任意形狀張量的平均值

A = torch.arange(6,dtype=torch.float32).reshape(2, 3)
A, A.mean(), A.sum() / A.numel()
"""
(tensor([[0., 1., 2.],[3., 4., 5.]]),tensor(2.5000),tensor(2.5000))
"""

計算平均值的函數也可以沿指定軸降低張量的維度

A.mean(axis=0), A.sum(axis=0) / A.shape[0]
"""
(tensor([1.5000, 2.5000, 3.5000]), tensor([1.5000, 2.5000, 3.5000]))
"""

6.3，非降維求和

調用函數來計算總和或均值時保持軸數不變會很有用
也就是keepdims=True，不會因為axis而把某個維度給去掉，而是置為一

A = torch.arange(6,dtype=torch.float32).reshape(2, 3)
sum_A = A.sum(axis=1, keepdims=True)
A, sum_A
"""
(tensor([[0., 1., 2.],[3., 4., 5.]]),tensor([[ 3.],[12.]]))
"""

keepdims默認為False，axis=1

a = torch.ones((2,5,4))
a.shape # torch.Size([2, 5, 4])
a.sum(axis=1).shape # torch.Size([2, 4])
a.sum(axis=1)
"""
tensor([[5., 5., 5., 5.],[5., 5., 5., 5.]])
"""
a
"""
tensor([[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]],[[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]]])
"""

keepdims默認為True，axis=1

a.sum(axis=1,keepdims=True).shape # torch.Size([2, 1, 4])
a.sum(axis=1,keepdims=True)
"""
tensor([[[5., 5., 5., 5.]],[[5., 5., 5., 5.]]])
"""

keepdims默認為False，axis=[0,2]

a.sum(axis=[0,2]).shape # torch.Size([5])
a.sum(axis=[0,2]) # tensor([8., 8., 8., 8., 8.])

keepdims默認為True，axis=[0,2]

a.sum(axis=[0,2],keepdims=True).shape # torch.Size([1, 5, 1])
a.sum(axis=[0,2],keepdims=True)
"""
tensor([[[8.],[8.],[8.],[8.],[8.]]])
"""

由于sum_A在對每行進行求和后仍保持兩個軸，我們可以通過廣播將A除以sum_A

A / sum_A
"""
tensor([[0.0000, 0.3333, 0.6667],[0.2500, 0.3333, 0.4167]])
"""

6.4，cumsum()

如果想沿某個軸計算A元素的累積總和，比如axis=0（按行計算）
可以調用cumsum函數。此函數不會沿任何軸降低輸入張量的維度

A = torch.arange(6,dtype=torch.float32).reshape(2, 3)
A, A.cumsum(axis=0)
"""
(tensor([[0., 1., 2.],[3., 4., 5.]]),tensor([[0., 1., 2.],[3., 5., 7.]]))
"""

7，點積

相同位置的按元素乘積的和
按元素乘法，然后進行求和來表示兩個向量的點積

x = torch.arange(4, dtype=torch.float32)
y = torch.tensor([2.0, 1, 4, 3])
x, y, torch.dot(x, y), torch.sum(x * y)
"""
(tensor([0., 1., 2., 3.]), tensor([2., 1., 4., 3.]), tensor(18.), tensor(18.))
"""

8，向量積

矩陣A和向量x調用torch.mv(A, x)時，會執行矩陣-向量積
A的列維數（沿軸1的長度）必須與x的維數（其長度）相同

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
x = torch.arange(4, dtype=torch.float32)
A, x, A.shape, x.shape, torch.mv(A, x)
"""
(tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),tensor([0., 1., 2., 3.]),torch.Size([5, 4]),torch.Size([4]),tensor([ 14.,  38.,  62.,  86., 110.]))
"""

9，矩陣乘法

矩陣A和矩陣B調用torch.mm(A, B)時，會執行矩陣乘法操作
前行成后列
A是一個5行4列的矩陣，B是一個4行3列的矩陣，兩者相乘后，得到了一個5行3列的矩陣

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = torch.tensor([[2,3,4],[1,5,9],[7,5,3],[4,5,6]],dtype=torch.float32)
A, B, torch.mm(A, B)
"""
(tensor([[ 0.,  1.,  2.,  3.],[ 4.,  5.,  6.,  7.],[ 8.,  9., 10., 11.],[12., 13., 14., 15.],[16., 17., 18., 19.]]),tensor([[2., 3., 4.],[1., 5., 9.],[7., 5., 3.],[4., 5., 6.]]),tensor([[ 27.,  30.,  33.],[ 83., 102., 121.],[139., 174., 209.],[195., 246., 297.],[251., 318., 385.]]))
"""

10，范數

一個向量的范數告訴我們一個向量有多大，這里考慮的大小（size）概念不涉及維度，而是分量的大小。

有Lp范數衍生出了L1、L2等范數，這些都是針對的向量
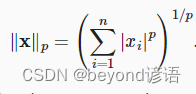
在這里插入圖片描述

10.1，L1范數

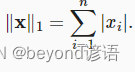
在這里插入圖片描述
L1范數：向量元素的絕對值之和
先通過絕對值函數，然后按元素求和

q = torch.tensor([10.0,14.0])
q, torch.abs(q).sum()
"""
(tensor([10., 14.]), tensor(24.))
"""

10.2，L2范數

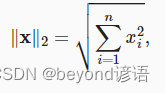
在這里插入圖片描述
L2范數：向量元素平方和的平方根
norm()函數進行求解

q = torch.tensor([3.0,4.0])
q, torch.norm(q)
"""
(tensor([3., 4.]), tensor(5.))
"""

10.3，Frobenius范數

Frobenius范數：矩陣元素平方和的平方根
norm()函數進行求解
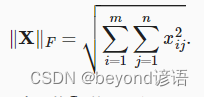
在這里插入圖片描述
Frobenius范數滿足向量范數的所有性質，它就像是矩陣形向量的L2范數

q = torch.tensor([[1.0,2.0],[3.0,4.0]])
q ,torch.norm(q)
"""
(tensor([[1., 2.],[3., 4.]]),tensor(5.4772))
"""

在深度學習中，經常試圖解決優化問題：最大化分配給觀測數據的概率; 最小化預測和真實觀測之間的距離。
用向量表示物品（如單詞、產品或新聞文章），以便最小化相似項目之間的距離，最大化不同項目之間的距離。
目標，或許是深度學習算法最重要的組成部分（除了數據），通常被表達為范數。

二、線性代數