最長公共子序列求序列模板提
Description:
描述：
This question has been featured in interview rounds of Amazon, MakeMyTrip, VMWare etc.
這個問題在亞馬遜，MakeMyTrip，VMWare等訪談輪次中都有介紹。
Problem statement:
問題陳述：
Given two strings str1 and str2, find length of the longest common sub-sequence between them
給定兩個字符串str1和str2 ，找到它們之間最長的公共子序列的長度
Let the strings be
str1="includehelp"
str2="letsinclude"
Output will be:
Longest common sub-sequence length is 7
The longest common sub-sequence is: "include"
The output is given above where the longest common sub-sequences is in same colour.
上面給出了最長公共子序列為相同顏色的輸出。
Solution Approach:
解決方法：
The problem can be solved in a brute-force way. By generating all sub-sequences and checking them whether equal or not. Finally taking the longest common subsequence. But undoubtedly this is not at all computable since generating all sub-sequence is itself exponential and then permutations for checking any two sub-sequences.
這個問題可以用蠻力解決。 通過生成所有子序列并檢查它們是否相等。 最后取最長的公共子序列。 但是毫無疑問，這根本不是可計算的，因為生成所有子序列本身就是指數的，然后進行排列以檢查任意兩個子序列。
The recursive way to solve is
遞歸的解決方法是
Let,
讓，
l1 = Length of the first string,str1
l2 = Length of the second string,str2
f(l1,l2) = Longest common subsequence length for string lengths l1 & l2
Now,
現在，
Think of the following example,
考慮以下示例，
Say first string is: x1 x2 ... xl1
假設第一個字符串是： x 1 x 2 ... x l 1
And the second string is: y1 y2 ... yl2
第二個字符串是： y 1 y 2 ... y l 2
Say,
說，
Then obviously we need to find LCS for the remaining part of string
那么顯然我們需要為字符串的其余部分找到LCS
Else
其他
Maximum of two case
最多兩種情況
LCS of the first string leaving character
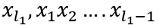and second string 第一個字符串離開字符的LCS
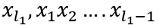和第二個字符串 LCS of the first string
and second string leaving character
第一個字符串的LCS
Now, we need to recur down to 0. So,
現在，我們需要遞歸降至0。因此，
Where base cases are,
在基本情況下，
If you generate this recursion tree, it will generate many overlapping sub-problems and thus, we need to reduce the re-computing. That’s why we need to convert it into dynamic programming where we will store the output of the sub-problems and we will use it to compute bigger sub-problems.
如果生成此遞歸樹，它將生成許多重疊的子問題，因此，我們需要減少重新計算。 這就是為什么我們需要將其轉換為動態編程，以便在其中存儲子問題的輸出，并使用它來計算更大的子問題。
轉換為動態編程 (Converting to Dynamic programing)
1) Initialize dp[l1+1][l2+1] to 0
2) Convert the base case of recursion:
for i=0 to l1
dp[i][0]=0;
for i=0 to l2
dp[0][i]=0;
3) Fill the DP table as per recursion.
for i=1 to l1 //i be the subproblem length for str1
for j=1 to l2 //j be the subproblem length for str2
if(str1[i-1]==str2[j-1]) //xl1==yl2
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
end for
end for
4) The final output will be dp[l1][l2]
C++ Implementation:
C ++實現：
#include <bits/stdc++.h>
using namespace std;
int max(int a, int b)
{
return (a > b) ? a : b;
}
int LCS(string str1, string str2)
{
int l1 = str1.length();
int l2 = str2.length();
int dp[l1 + 1][l2 + 1];
for (int i = 0; i <= l1; i++)
dp[i][0] = 0;
for (int i = 0; i <= l2; i++)
dp[0][i] = 0;
for (int i = 1; i <= l1; i++) {
for (int j = 1; j <= l2; j++) {
if (str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[l1][l2];
}
int main()
{
string str1, str2;
cout << "Enter first string\n";
cin >> str1;
cout << "Enter Second string\n";
cin >> str2;
cout << "Longest Common sub-sequence length is: " << LCS(str1, str2) << endl;
return 0;
}
Output
輸出量
Enter first string
includehelp
Enter Second string
letsincludeus
Longest Common sub-sequence length is: 7
翻譯自: https://www.includehelp.com/icp/longest-common-subsequence.aspx
最長公共子序列求序列模板提
)
