目錄
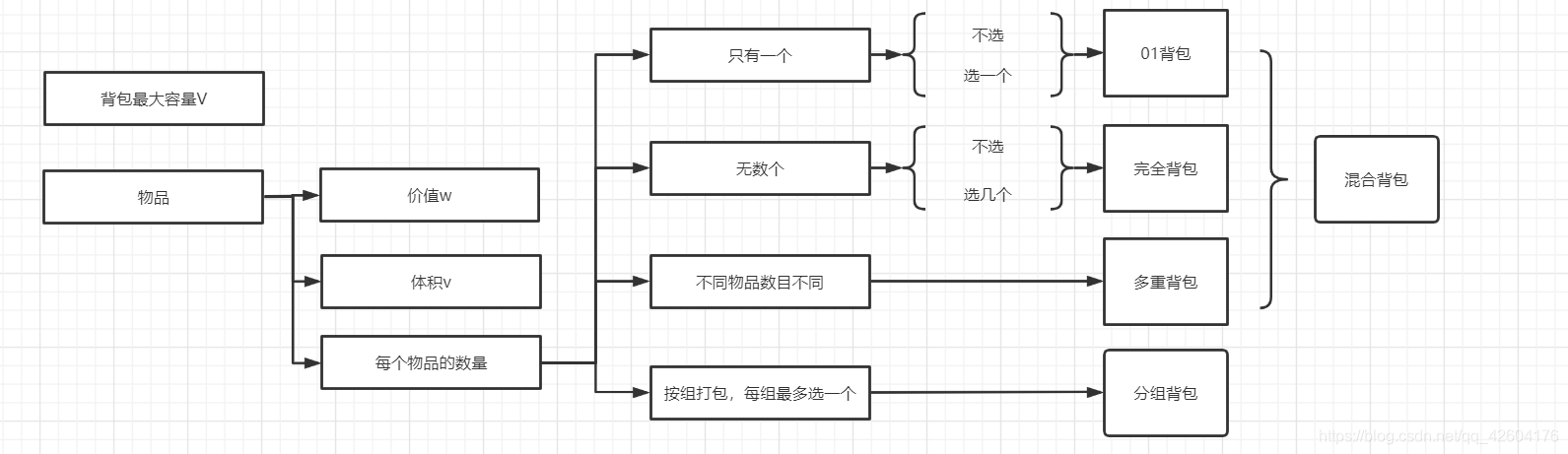
- 01背包
- [416. 分割等和子集](https://leetcode-cn.com/problems/partition-equal-subset-sum/)
- [1049. 最后一塊石頭的重量 II](https://leetcode-cn.com/problems/last-stone-weight-ii/)
- [494. 目標和](https://leetcode-cn.com/problems/target-sum/)
01背包
1、dp數組以及下標含義
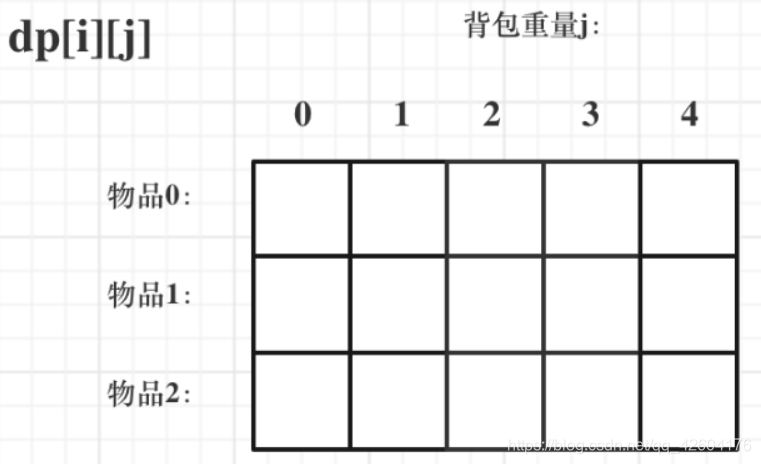
dp[i][j]標識從下標為[0,1]的物品里任意取,放進容量為j的背包,價值總和最大是多少?
2、確定遞推公式
dp[i][j]可以由兩個方向推出:
1、dp[i-1][j],背包容量為j,里面不放入物品i的最大價值,此時dp[i][j] = dp[i-1][j]
2、dp[i-1][i-weight[i]]推出,背包容量為i-weight[i]的時候此時dp[i][j] = dp[i-1][j-weight[i]]+valuep[i];
所以遞推公式為:
dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
3、dp數組如何初始化
關于初始化,一定要和dp數組的定義吻合。
如果背包容量j為0的話,dp[i][0]無論是選取哪些物品,背包價值總和一定為0。
由遞推可知i是由i-1推出來的,那么i為0時一定要初始化。
dp[0][j]存放編號為0的物品時,各個容量的背包能存放的最大價值:
for(int j = bagWeight; j >= weight[0]; j--)
{dp[0][j] = dp[0][j-weight[0]] + value[0];
}
這里需要注意,初始化是倒序遍歷。
dp[0][j]表示容量為j的背包存放物品0時候的最大價值。由于每個物品只有1個,如果dp[0][j]必須為初值,正序遍歷,物品0會被重復加入多次。
dp[i][j]在推導的時候一定是取價值最大的數,如果題目給的價值都是正整數,那么下標初始化為0.如果價值里面有負數,初始化為負無窮。只要保證dp數組在遞推公式的過程中取最大的價值,而不是被初始值覆蓋。
所以dp數組初始化如下:
vector<vector<int>> dp(weight.size() + 1,vector<int>(bagWeight + 1,0));
for(int j = bagWeight; j >= weight[0]; j--)
{dp[0][j] = dp[0][j-weight[0]] + value[0];
}
4、確定遍歷順序
有兩個遍歷維度:物品與背包重量,先遍歷物品更好理解。
for(int i = 1; i < weight.size(); i++) //遍歷物品
{for(int j = 0; j <= bagWeight; j++) //遍歷背包容量 { if(j < weight[i]) dp[i][j] = dp[i-1][j]; //else dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+values[i])}
}
滾動數組優化
1、確定dp數組的定義
dp[j]:容量為j的背包,所背的物品價值可以最大為dp[j]。
2、一維dp遞推公式
dp[j]可以通過dp[j-weight[i]]推導,其表示容量為j-weight[i]的背包所背的最大價值。
dp[j-weight[i]]+value[i]表示容量為j-物品i重量的背包加上物品i的價值。(即容量為j的背包放入物品i之后的價值)此時dp[j]有兩個選擇,一個是取自己dp[j],一個是取dp[j-weight[i]]+value[i].
所以遞推公式為:
dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);
3、初始化
假設物品價值都是大于0的,dp數組初始化的時候都初始化為0
4、確定遍歷順序
for(int i = 0; i < weight.size(); i++) //遍歷物品
{for(int j = bagWeight; j >= weight[i]; j--) //遍歷背包容量{dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);}
}二維遍歷時,背包容量從小到大,一維遍歷,背包容量從大到小。
這是因為倒序遍歷是為了保證物品i只被放入一次。二維dp,dp[i][j]是通過上一層dp[i-1][j]計算得到的,所以本層的dp[i][j]并不會產生覆蓋。
一維01背包測試代碼:
void test_one_dim_01bag()
{vector<int> weight = {1,3,4};vector<int> value = {15,20,30};int bagWeight = 4;//初始化vector<int> dp(bagWeight+1,0);for(int i = 0; i < weight[i]; i++) //遍歷物品{for(int j = bagWeight; j >= weight[i]; j--) //遍歷背包容量{dp[j] = max(dp[j],dp[j-weight[i]] + value[i]);}}cout << dp[bagWeight] << endl;
}
416. 分割等和子集
求集合里是否出現總和為sum/2的子集。
背包體積為sum/2
背包放入的商品的重量為元素的數值,價值也為元素的數值
背包如何正好被裝滿,說明找到了總和為sum/2的子集
背包中每個元素都是不可重復放入的。
1、確定dp數組以及下標含義
dp[j]表示容量為j的背包,所背物品價值可以最大為dp[j]。
dp[j]表示背包總容量為j,最大可以湊成j的子集總和為dp[j]。
2、確定遞推公式
dp[j] = max(dp[j],dp[j-nums[i]] + nums[i]);
3、初始化
vector<int> dp(target+1,0); //target為背包容量
4、確定遍歷順序
for(int i = 0; i < nums.size(); i++)
{for(int j = target; j >= nums[i]; j--){dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);}
}
AC代碼:
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for(int num : nums){sum += num;}if(sum % 2 != 0) return false;int target = sum / 2;vector<int> dp(target+1,0);for(int i = 0; i < nums.size(); i++){for(int j = target; j >= nums[i]; j--){dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);if(dp[j] == target) return true;}}if(dp[target] == target) return true;else return false;}
};
1049. 最后一塊石頭的重量 II
將石頭盡量分成兩堆相同重量,然后相撞。分成兩堆的思路與上一題一致。
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for(int stone : stones){sum += stone;}int target = sum / 2;//dp[target],容量為target的背包最多能背多重的石頭vector<int> dp(target+1,0);for(int i = 0; i < stones.size(); i++){for(int j = target; j >= stones[i]; j--){dp[j] = max(dp[j],dp[j-stones[i]] + stones[i]);}}return sum - dp[target]*2;}
};
494. 目標和
所有數字可以分為兩堆,一堆符號為正,一堆符號為負。
pos + neg = S 且 pos - neg = sum
所以pos = (S+sum)/2,問題轉化為集合nums中找出和為pos的組合。
此時問題就轉化為,裝滿容量為pos背包,有幾種方法。
這次和之前遇到的背包問題不一樣了,之前都是求容量為j的背包,最多能裝多少。
本題則是裝滿有幾種方法。其實這就是一個組合問題了。
1、確定dp數組以及下標
dp[j]表示,填滿體積為j的背包,有dp[j]種方法。
2、確定遞推公式
不考慮nums[i],填滿容量為j-nums[i]的背包,有dp[j-nums[i]]種方法,
如果能搞到nums[i],則填滿容量為j-nums[i]的背包,就有dp[j]+dp[j-nums[i]]種方法。
dp[j] += dp[j-nums[i]]
3、初始化dp數組
dp[0] = 1,裝滿容量為0的背包,有1種方法。其他dp[i]均設置為0,在不知道nums[i]的情況下,沒有方法。
4、確定遍歷順序
nums外循環,j內循環倒序。
AC代碼:
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for(int num : nums)sum += num;//如果絕對值和比targetabs小,說明都用同一個符號也不能湊成if(sum < abs(target)) return 0;//如果不能完整的分成兩組,那么說明沒有方法if((target + sum) % 2 == 1) return 0;int bagWeight = (target + sum)/2;vector<int> dp(bagWeight+1,0);dp[0] = 1;for(int i = 0; i < nums.size(); i++){for(int j = bagWeight; j >= nums[i]; j--){dp[j] += dp[j-nums[i]];}}return dp[bagWeight];}
};





? ACK代表什么?)




--為沙盒解決方案創建自定義活動...)



![[LeetCode] Maximal Rectangle](http://pic.xiahunao.cn/[LeetCode] Maximal Rectangle)


)

