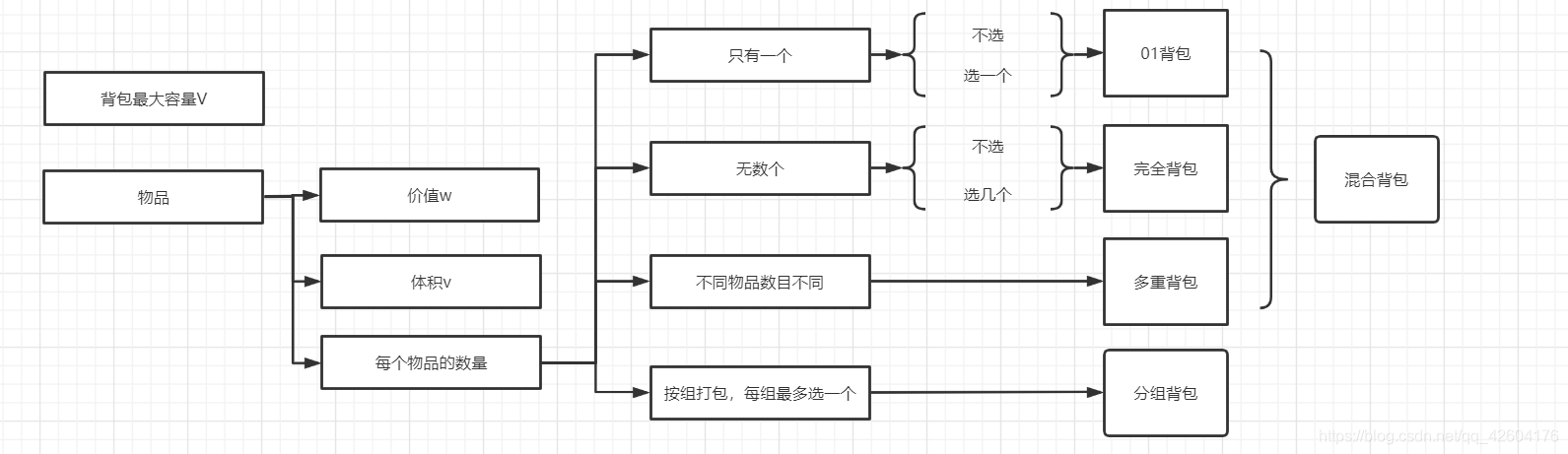
N件物品和一個最多能背重量為W的背包。第i件物品的重量為weight[i],得到的價值是value[i]。每件物品都有無限個(可以放入背包多次),求解將哪些物品裝入背包里物品價值總和最大。
01背包和完全背包唯一不同在于遍歷順序上。
01背包的核心代碼:
for(int i = 0; i < weight.size(); i++) //遍歷物品
{for(int j = bagWeight; j >= weight[i]; j--) //遍歷背包容量{dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);}
}
內嵌的循環是從大到小遍歷,為了保證每個物品僅僅被添加一次。而完全背包的物品是可以添加多次的,所以要從小到大去遍歷。
for(int i = 0; i < weight.size(); i++) //遍歷物品
{for(int j = weight[i]; j <= bagWeight; j++) //遍歷背包容量{dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);}
}
leetcode題目
- [518. 零錢兌換 II](https://leetcode-cn.com/problems/coin-change-2/)
- [377. 組合總和 Ⅳ](https://leetcode-cn.com/problems/combination-sum-iv/)
- 爬樓梯變形
- [322. 零錢兌換](https://leetcode-cn.com/problems/coin-change/)
- [279. 完全平方數](https://leetcode-cn.com/problems/perfect-squares/)
- [139. 單詞拆分](https://leetcode-cn.com/problems/word-break/)
518. 零錢兌換 II
這一題與https://blog.csdn.net/qq_42604176/article/details/116051902?spm=1001.2014.3001.550101背包中的組合問題有相似之處。只需要把遍歷順序修改就行了。
step1: dp[j]:湊成總金額j的貨幣組合數為dp[j]
step2: dp[j] += dp[j - coins[i]];
step3: 湊成總金額0的貨幣組合數為1。
step4:使用完全背包的遍歷方式,注意由于是求組合數,內外嵌套需要注意。
AC代碼如下:
class Solution {
public:int change(int amount, vector<int>& coins) {int sum = 0;vector<int> dp(amount+1,0);dp[0]=1;for(int i = 0; i < coins.size(); i++){for(int j = coins[i]; j <= amount; j++){dp[j] += dp[j-coins[i]];}}return dp[amount];}
};
代碼隨想錄公眾號做出的這個總結很好,雖然現在還沒有完全理解是為什么:
如果求組合數就是外層for循環遍歷物品,內層for遍歷背包。
如果求排列數就是外層for遍歷背包,內層for循環遍歷物品。
377. 組合總和 Ⅳ
如果本題要把排列都列出來的話,只能使用回溯算法爆搜。
但是它只要求我們得到排列方法的數目。由于可以重復取,所以使用完全背包。由于是求排列數,外層for循環遍歷背包,內層for循環遍歷元素。
最內層需要對兩個數相加小于INT_MAX進行限制。
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target+1,0);dp[0] = 1;for(int i = 0; i <= target; i++) //遍歷背包容量{for(int j = 0; j < nums.size(); j++) //遍歷物品{if(i >= nums[j] && dp[i] < INT_MAX - dp[i-nums[j]])dp[i] += dp[i-nums[j]]; }}return dp[target];}
};
爬樓梯變形
假設你正在爬樓梯。需要 n 階你才能到達樓頂。每次可以爬 1 、 2或者m 個臺階。問有多少種不同的方法可以爬到樓頂呢?
分析:1階,2階,m階就是物品,樓頂就是背包。每一階可以重復使用,例如跳了1階,還可以繼續跳1階。所以這是一個完全背包問題。
step1 : dp[i]爬到有i個臺階的樓頂,有dp[i]種方法。
step2: dp[i] += dp[i-j];
step3: dp[0] = 1,dp[…]=0;
step4:遍歷順序,由于是排列問題,1、2與2、1是不一樣的,所以將背包容量放在外層循環,將物品放到內層循環。又因為是完全背包問題,所以從前向后遍歷。
int climbStairs(int n,int m)
{vector<int> dp(n+1,0);dp[0]=1;for(int i = 0; i <= n; i++){for(int j = 0; j <= m; j++)if(i -j >= 0) dp[i] += dp[i-j];}return dp[n];
}
322. 零錢兌換
step1:dp[j]湊足金額為j所需要的錢幣的最少個數為dp[j]
step2:dp[j] = min(dp[j-coins[i]]+1,dp[j]);
step3:湊足金額為0的所需金幣個數為0,即dp[0]=0;其他初值為INT_MAX。
湊足金額為j-coins[i]的最少個數為dp[j-coins[i]],那么只需要加上一個錢幣coins[i]即dp[j-coins[i]]+1就是dp[j].
step4:求最小個數,錢幣有順序無順序都可以,都不影響錢幣的最小個數。
求組合數,for外層遍歷物體,for內層遍歷背包。求排列,外層for遍歷背包,內層for循環遍歷物品。
本題兩者均可。
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,INT_MAX);dp[0] = 0;for(int i = 0; i < coins.size(); i++) //物品{for(int j = coins[i]; j <= amount; j++) //背包容量{//如果為初值,跳過,沒有必要計算,而且計算會溢出if(dp[j-coins[i]] == INT_MAX) continue;dp[j] = min(dp[j-coins[i]]+1,dp[j]);}}//如果沒有被賦值,那么說明沒有解,返回-1if(dp[amount] == INT_MAX) return -1;return dp[amount];}
};
279. 完全平方數
完全平方數就是物品(無限使用),湊成的正整數n就是背包。問湊滿背包最少有多少個物品。
step1:dp[j],湊滿容量為j的背包最少物品數目。
step2:dp[j] = min(dp[j-i*i] +1,dp[j]);
step3: dp[0] = 0;雖然0符合完全平方數要求,但是題目要求是從1開始找完全平方數。其余下標的dp初始值為INT_MAX
step4:對于求最小方法數的,內外層不需要管循環。
class Solution {
public:int numSquares(int n) {vector<int> dp(n+1,INT_MAX);dp[0] = 0;for(int i = 1; i <= n; i++){for(int j = i*i; j <= n; j++){if(dp[j-i*i] == INT_MAX) continue;dp[j] = min(dp[j-i*i]+1,dp[j]);}}return dp[n];}
};
139. 單詞拆分
物品:wordDict中的string,可以重復取
背包:s字符串
step1: dp[i]:字符串長度為i,dp[i]為true,表示可以拆分一個或者多個在字典中出現的單詞。
step2: 如果dp[j]為true,則[j,i]這個區間的子串出現在字典里,那么dp[i]一定為true。
所以遞推公式為;
if(wordSet.find(s.substr(j,i-j)) != wordSet.end() && dp[j]) dp[i] = true;
step3:dp[0]字符串為0,為了方便推導公式,我們只好給他true,不然公式推導下去全為false。
step4:由于是求最小方法數,所以內外層遍歷順序無需在意
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {//將vector放入set中,加快查詢unordered_set<string> wordSet(wordDict.begin(),wordDict.end());vector<bool> dp(s.size()+1,false);dp[0] = true;for(int i = 0; i <= s.size(); i++) //背包容量{for(int j = 0; j <= i; j++) //物品{string str = s.substr(j,i-j); if(wordSet.find(str) != wordSet.end() && dp[j] == true){dp[i] = true;}}}return dp[s.size()];}
};



? ACK代表什么?)




--為沙盒解決方案創建自定義活動...)



![[LeetCode] Maximal Rectangle](http://pic.xiahunao.cn/[LeetCode] Maximal Rectangle)


)



