多重背包簡介：
有N種物品和一個容量為V的背包。第i種物品最多有Mi件可用，每件耗費的空間為Ci，價值為Wi。求解將哪些物品裝入背包可使得這些物品耗費的空間總和不超過背包容量，且價值總和最大。
將Mi件攤開，就是一個01背包問題。
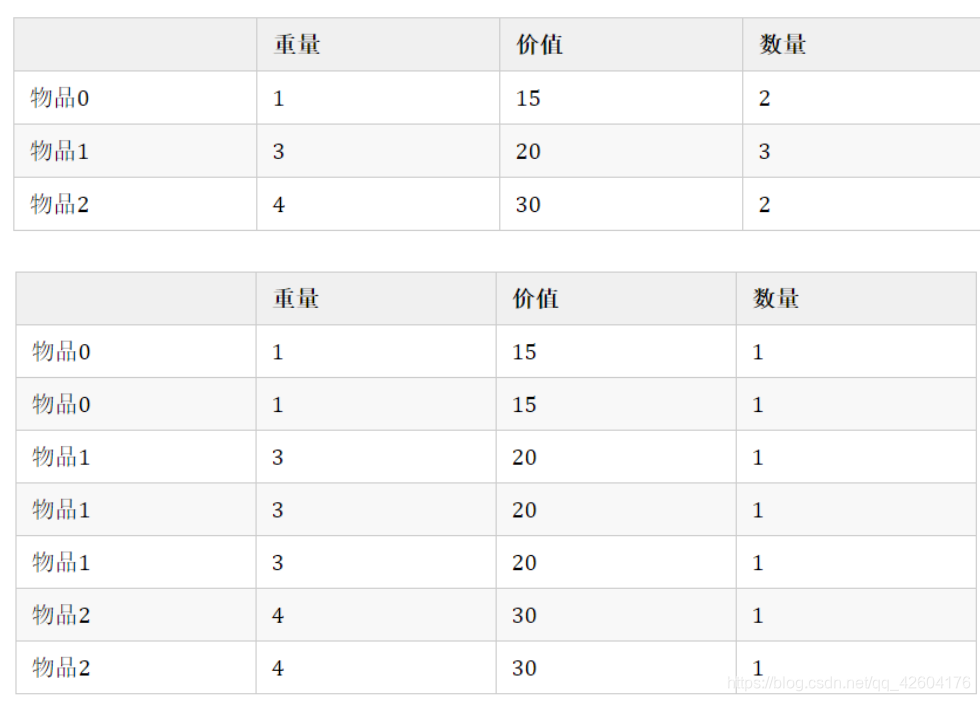
如下列兩表就是等價的，圖來源于代碼隨想錄。

void test_multi_pack() 
{vector<int> weight = {1,3,4};vector<int> value = {15,20,30};vector<int> nums = {2,3,2};int bagWeight = 10;//進行展開，轉化為01背包問題for(int i = 0; i < nums.size(); i++){while(nums[i] > 1)	{//nums[i]保留到1，把其他的多余的個數展開weight.push_back(weight[i]);value.push_back(value[i]);nums[i]--;}}vector<int> dp(bagWeight + 1, 0);for(int i = 0; i < weight.size(); i++)	//遍歷物品{for(int j = bagWeight; j >= weight[i]; j--)	//遍歷背包容量{dp[j] = max(dp[j],dp[j-weight[i]] + values[i])}}cout << dp[bagWeight] << endl;
}