本系列筆記為方便日后自己查閱而寫,更多的是個人見解,也算一種學習的復習與總結,望善始善終吧~
一階常系數微分方程
Au=dudt
將一階常系數微分方程轉換為線性代數問題的關鍵在于常系數微分方程的解一定是指數形式的。那么我們的需要求解的東西就是指數的系數和指數的冪,而這可以轉換為線性代數問題。
解的指數形式通常是自然常數e的指數(猜測是因為時域信號可以轉到頻域,傅里葉變換,這方面學識淺薄)
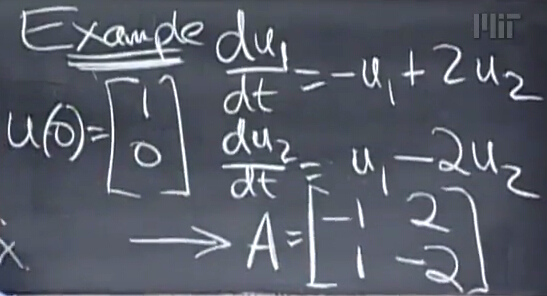
這個形式很容易讓我們聯想到之前對于矩陣A的冪的求解,這里看一個例子:
這里問題被轉換為了求解Au=dudt
特征值與特征向量
先找A的特征值和特征向量
求解特征值
兩個小技巧:
- 行列式determinant為特征值的積
- 矩陣的跡trace為特征值的和
當然可以直接求解determinant=0得到特征值:
由于老師直接劇透e的冪系數中為矩陣A的特征值,那么對于特征值-3來說,隨著t的增加,最終這一項為0;而對于特征值0來說,隨著t增加,最終這一項為某一個確定值(解會收斂);舉一反三:對于特征值大于0,隨著t增加,解發散。
求解特征向量
兩個小技巧:
- 對于特征值為0,特征向量即為null space,free variable自由變量置1很容易求得
- 對于另一個特征值-3,利用A?λI特征向量不變,也可以轉換為求解null space
解的形式
解會是上面這樣的形式,證明:
帶入之前的公式dudt=Au
?λ1eλ1tx1=Aeλ1tx1
?λ1x1=Ax1
于是,我們可以將剛才求解出的特征值與特征向量帶入式子:
現在,我們只需要求解c1,c2,這可以通過初值u(0)求解,在t=0時:
口算都能得出答案是c1=c2=13
得到最終的解
所以,當時間趨于無窮時,進入穩態steady state(自動控制的名詞都來了,汗)
首先是關于穩定,我們已經知道的是特征值小于0時,隨著時間增加,相關項變為0,所以當特征值都小于0時,隨著時間增加最終趨近于0;現在我們想要知道當特征值有復數的時候會怎么樣?
對于復數,其虛數部分的模norm為1,影響忽略不計,所以現在我們知道要想穩定,則特征值的實數部分應當小于0,虛數部分無所謂。很明顯:當其中一個特征值為0時,有一個穩態值steady state;當存在特征值大于0時,隨著時間增加,值發散。
看一下這樣的結論對于我們比較關注的2x2矩陣有什么指導意義:
要想最終穩定,要有特征值都小于0,所以矩陣的跡trace大于0,矩陣的行列式determinant小于0
特征分解
我們的方程表明兩個變量相互耦合,特征值和特征向量的作用就在于可以實現解耦(又稱對角化)。
如何實現呢?先看我們的特征分解A=SΛS?1
要實現解耦的關鍵在于將u=Sv帶入原方程
dudt=Au
?Sdvdt=ASv
?dvdt=S?1ASv
?dvdt=Λv
?dv1dt=Λv1
這樣的方程用之前的結論求解,得:
老師的目的是得到結論以引出下一個環節(于是這里果斷沒看懂):
關于eAt
要了解自然常數的矩陣次冪,我們最好把它展開。
泰勒級數展開:
其對于的矩陣形式:
下面的式子可以在t很小時求解矩陣的逆,當可以注意到,上面的式子最終總會收斂,而下面的式子只有當At的特征值的絕對值小于1才能收斂。這里我們只關注上面的式子。
帶入特征分解的公式:
將I=SS?1,化簡得eAt=SeλtS?1,這些公式成立的前提是A可以對角化.
從這個角度來觀察我們之前的情況:
u(t)=SeΛtS?1u(0)
我們可以得到一樣的結論,這里的結論比之前更為一般化,為了直觀了解,畫出來:
左半平面,特征值的實數部分小于0,最終會有一個穩態值steady state;什么時候穩態值為0?特征值的絕對值都小于1時(之前泰勒展開的結論),這張圖很像根軌跡圖有木有?!
關于二階微分方程
利用一些小技巧,換成我們熟悉的樣子,現在關鍵在于找到矩陣A:
手寫可以寫出來啦:
推廣到N階(這里以5階為例):
矩陣A第一行為原方程的系數,底下類似單位矩陣。
這樣就可以轉化為我們熟悉的一階微分方程了、
PS:另一位仁兄的筆記
http://blog.csdn.net/suqier1314520/article/details/14053183
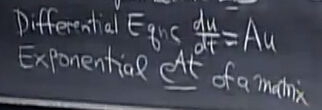

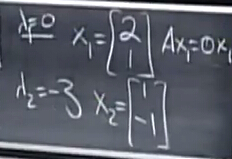
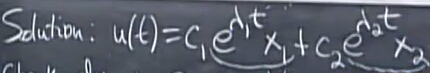
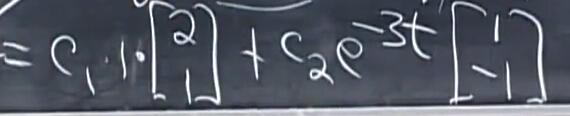
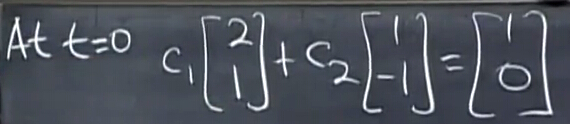
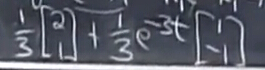
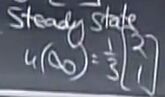
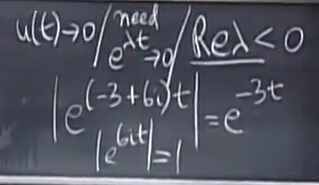
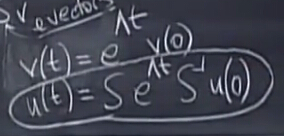
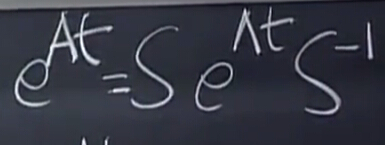
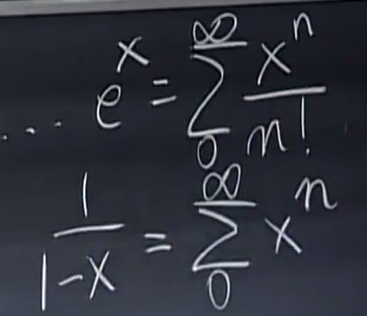
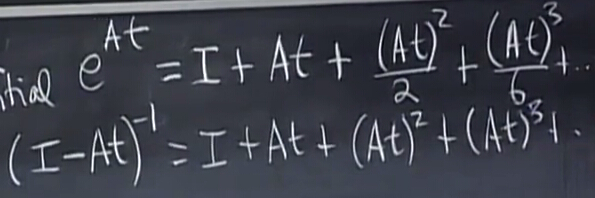
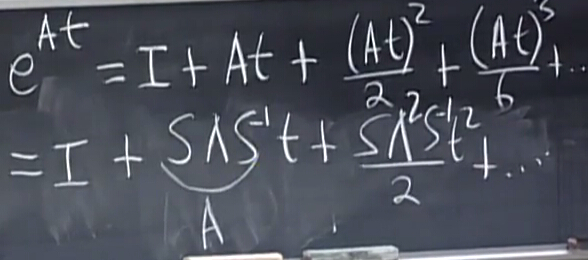
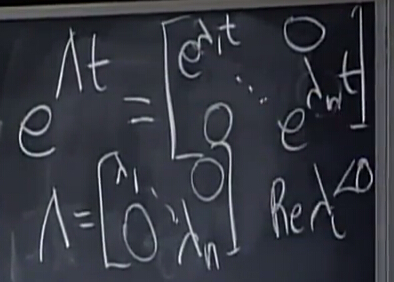
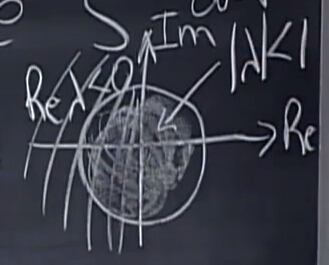
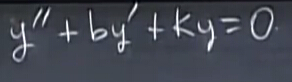
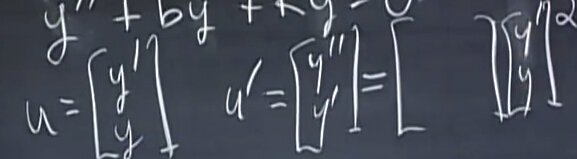
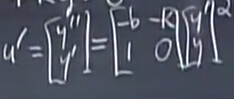
![Win32ASM學習[21]:宏匯編(1)](http://pic.xiahunao.cn/Win32ASM學習[21]:宏匯編(1))





)



![Win32ASM學習[23]:RadASM快捷鍵](http://pic.xiahunao.cn/Win32ASM學習[23]:RadASM快捷鍵)








![Win32ASM-進程學習[3]-讀寫進程空間](http://pic.xiahunao.cn/Win32ASM-進程學習[3]-讀寫進程空間)