[回歸分析][10]--相關誤差的問題
? 這一篇文章還是來分析相關誤差的問題。
?
?1.游程數
? 定義:游程數--殘差穿過x-軸的次數
? 用這個可以檢查如殘差有一塊在x軸上面,一塊在x軸下面的情形。
?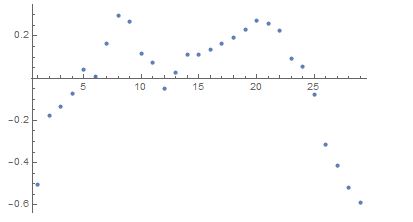
如上面這樣的殘差
下面構造兩個統計量:
?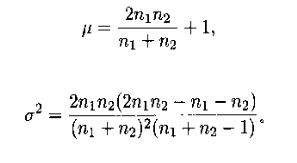
其中 n1=殘差為正的個數?? n2=殘差為負的個數,可以用上面的公式計算出當n1,n2為給定數時的均值與方差

2.D-W統計量
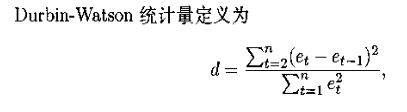
上面是定義

這是d與p的關系,p代表相關系數,則由這個表達式可以看出d越接近2是越不相關的,即p==0.
如何修改的話,要根據情況而定,可能還需要增加變量個數。
以上,所有
2016/11/28
?
?1.游程數
? 定義:游程數--殘差穿過x-軸的次數
? 用這個可以檢查如殘差有一塊在x軸上面,一塊在x軸下面的情形。
?

如上面這樣的殘差
下面構造兩個統計量:
?
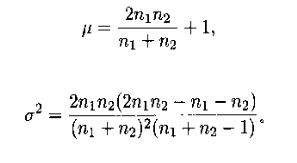
其中 n1=殘差為正的個數?? n2=殘差為負的個數,可以用上面的公式計算出當n1,n2為給定數時的均值與方差
cancha = lm["StandardizedResiduals"];
RunLength[cancha_List] := Block[{n1, n2, u, v2, youcheng, ycn},n1 = Length[Select[cancha, # >= 0 &]];n2 = Length[Select[cancha, # < 0 &]];u = (2.*n1*n2/(n1 + n2)) + 1;v2 = (2.*n1*n2*(2*n1*n2 - n1 - n2))/((n1 + n2)^2*(n1 + n2 - 1));youcheng = {};For[i = 1, i <= Length[cancha], i++,If[cancha[[i]] >= 0, youcheng = AppendTo[youcheng, 1], youcheng = AppendTo[youcheng, -1]];];ycn = 0;For[i = 1, i <= Length[youcheng] - 1, i++,If[youcheng[[i + 1]] - youcheng[[i]] != 0, ycn = ycn + 1];];Grid[{{"期望", " | ", "方差", " | ", "游程數"}, {u, " | ", v2, " | ", ycn}}, Frame -> True]]
{{0.09, 2.2}, {0.09, 2.22}, {0.1, 2.24}, {0.1, 2.27}, {0.1,2.28}, {0.1, 2.29}, {0.11, 2.29}, {0.11, 2.29}, {0.11, 2.3}, {0.11, 2.3}, {0.11, 2.3}, {0.11, 2.34}, {0.11, 2.39}, {0.12, 2.43}, {0.12,2.48}, {0.12, 2.53}, {0.12, 2.58}, {0.12, 2.61}, {0.12, 2.63}, {0.13, 2.66}, {0.13,2.68}, {0.13,2.71}, {0.13,2.74}, {0.14, 2.77}, {0.14, 2.79}}
2.D-W統計量
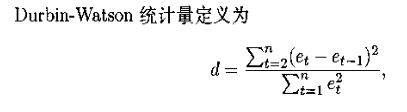
上面是定義

這是d與p的關系,p代表相關系數,則由這個表達式可以看出d越接近2是越不相關的,即p==0.
lm["DurbinWatsonD"]如何修改的話,要根據情況而定,可能還需要增加變量個數。
以上,所有
2016/11/28






)

)





)
詳解)
)


