1. 裝配線平衡模型
一個裝配線含有一系列的工作站。在終于產品的加工過程中每一個工作站運行一種或者是幾種特定的任務。裝配線周期是指全部工作站完畢分配給他們各自任務所花費時間的最大值。平衡裝配線的目標是為每一個工作站分配加工任務。盡可能使每一個工作站運行同樣數量的任務。其終于標準是轉配線周期最短。
不適當的平衡裝配線將會產生瓶頸——有較少任務的工作站將被迫等待前面分配了較多任務的工作站。
這個模型的目標是最小化裝配線周期。有兩類約束:
(1)要保證每件任務僅僅能也必須分配至一個工作站來加工;
(2)要保證滿足任務件的全部優先關系。
例? 有1件任務(A-K)分配到四個工作站(1-4),任務按次序例如以下。每件任務所花時間例如以下
| 任務 | 時間 |
| A | 45 |
| B | 11 |
| C | 9 |
| D | 50 |
| E | 15 |
| F | 12 |
| G | 12 |
| H | 12 |
| I | 12 |
| J | 8 |
| K | 9 |
?
這里給出求解模型
model:!裝配平衡模型;
sets:!任務集合,有一個完畢時間屬性T;TASK/A B C D E F G H I J K/:T;!人物之間的優先關系集合;PRED(TASK,TASK)/A,B B,C C,F C,G F,J G,J J,KD,E E,H E,I H,J I,J/;!工作站集合;STATION/1..4/;TXS(TASK,STATION):X;!X是派生集TXS的一個屬性。假設X(I,K)=I,則表示第I個任務指派給第K個工作站完畢; endsets data: !任務A B C D E F G H I J K的完畢時間預計例如以下; enddata !當任務超過15個時,模型求解將變的非常慢: !每個作業必須指派到一個工作站中; @for(TASK(I):@SUM(STATION(K):X(I,K))=1); !對于每個存在有限關系的作業來說。前者相應的工作站I必須小于后者相應的工作站J; @for(PRED(I,J):@sum(STATION(K):K*X(J,K)-K*X(I,K))>=0); !對于每個工作站來說,其花費時間不應大于裝配線周期; @for(STATION(K): @SUM(TXS(I,K):T(I)*X(I,K))<+CYCTIME); !目標函數時最小化轉配線周期; min=CYCTIME; !指定X(I,J)為0/1變量; @for(TXS:@BIN(X)); end
?
?
2.旅行售貨員問題,又稱貨郎擔問題
有一個銷售員,從城市1出發。要遍訪城市2,3,。。
。,n個一次。最后返回城市1.已知從城市i到j的旅費為Cij,問他該按如何的次序訪問這些城市,是得總旅費最少?能夠用多中方方法把TSP表示成整數規劃模型。把該問題的每個解看做時一個巡回。
在上述意義下,引入0-1整數變量
?
經過若干證明。這里就不在闡述了,我們能夠把TSP轉化為一個混合整數規劃問題
?
?
?這里我們能夠利用這個問題來求解一個詳細問題
?問題1? 現須要一臺機器上加工n個零件。這些零件能夠依照隨意先后順序在機器上進行加工。我們希望加工完畢全部零件的總時間最小。因為加工工藝的要求,加工零件j時機器不許處在對應的狀態Sj(如爐溫)。設起始未加工不論什么零件時機器處于狀態S0。且當全部零件加工完畢后需回復到S0狀態。已知從狀態Si調整到Sj須要時間Cij。零件j本身加工時間為Pj。
為方便起見,引入一個徐零件0,當中加工時間為0。要求狀態為S0。則{0,1,2,。。
。
,n}的一個圈置轉換pi就表示對全部零件的一個加工順序。則完畢全部加工所需時間為
?
這里給出一個解決該模型的一個簡單的代碼。就是套用上面的模型
!旅行售貨員問題;
model:
sets:city/1..5/:u;link(city,city):dist,x;
endsetsn=@size(city);
data:dist=@qrand(1);!隨即產生。這里能夠改為你要解決的問題的數據;
enddata!目標函數;
min=@sum(link:dist*x);
@for(city(K):@sum(city(I)|I#ne#K:x(I,K))=1;@sum(city(J)|J#ne#K:x(K,J))=1;
);!保證不出圈子;
@for(city(I)|I#gt#1:@for(city(J)|J#gt#1 #and# I#ne#j:u(I)-u(J)+n*x(I,J)<=n-1);
);
!定義X為0/1變量;
@for(link:@bin(x));
end
3.最短路問題
給定N個點Pi組成集合{Pi}。由集合中任一點Pi到還有一點Pj的距離用Cij表示,假設Pi到Pj沒有弧連接,則規定Cij=正無窮大,有規定Cii=0,指定一個終點PN。要求從Pi到PN的最短路線。這里我們用動態規劃的方法來做。
?
?又LINGO我們能夠非常方便的求解上述的模型
!最短路問題;
model:
data:n=10;
enddata
sets:cities/1..n/:F;roads(cities,cities)/1,2 1,32,4 2,5 2,63,4 3,5 3,64,7 4,85,7 5,8 5,96,8 6,97,108,109,10
/:D,P;
endsets
data:
D=6 5 !該矩陣即為傳說中的權重矩陣3 6 97 5 119 18 7 54 10579;
enddata
F(n)=0;
@for(cities(i)|i#lt#n:F(i)=@min(roads(i,j):D(i,j)+F(j));
);
!顯然。假設P(i,j)=1,則點i到點n的最短路徑的第一步是i——j,否則就不是
由此,我們就可方便的確定出最短路徑;
@for(roads(i,j):P(i,j)=@if(F(i)#eq#D(i,j)+F(j),1,0)
);
end?
4.分配問題或稱指派問題
這是給n個人分配n項工作以或得摸個最高效果的問題。
第i個人完畢第j項工作須要的平均時間為Cij。
要求給每一個人分配一項工作。并要求分配完這些工作,以使完畢所有任務的總時間最小。該問題能夠表演示樣例如以下
?
?這個模型能夠用LINGO非常方便的求解
model:!7個工人,7個工作的分配問題;
sets:workers/w1..w7/;jobs/j1..j7/;links(workers,jobs):cost,volume;
endsets!目標函數;min=@sum(links:cost*volume);!每一個人僅僅能有一份工作;@for(workers(I):@sum(jobs(J):volume(I,J))=1;);
data:cost=6 2 6 7 4 2 54 9 5 3 8 5 85 2 1 9 7 4 37 6 7 3 9 2 72 3 9 5 7 2 65 5 2 2 8 11 49 2 3 12 4 5 10;
enddata
end ?
5.二次分配問題
這個問題與上面的分配問題?。大致相同。相同要引入0-1變量,并且和上述問題有相同的約束?。可是本問題又比約束問題要復雜。我們得到價格系數Cijkl,其解釋是:在i(S上網一個元素)分配給j(T的一個元素)的同一時候把k(s的一個元素)分配給l(T的一個元素)所應承擔的費用。顯然僅僅有當xij=1且xkl=1時,才承擔這樣的費用。
這時我們的模型要變成這樣
?為了理解這個模型。我們在這里增加這個樣例。
首先覺得S是一個工廠的集合。T是n個城市的集合。本問題就是要在每個城市設置一個工廠,并要使工廠之間的總得通訊費用最少。通訊費用取決于:(1)每對工廠之間通訊的次數tik;(2)每對工廠所在兩個城市之間的距離djl。所以就有cijkl=tik*djl(各位大仙湊活的看啊。。。)。
因此總費用能夠用上述的目標函數來表示。
這里給出一個非常經典的題目,也是我遇到的第一道建模問題。想當年不知道lingo的優點。硬是憑著對C++的執拗,用了一堆棧啊。鏈表向量什么的用窮舉給退出來啊,當時多么的自豪。哈哈哈
?
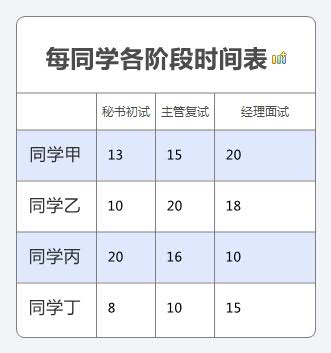
例:有四名同學到一家公司去參加三個階段的面試:公司要求每一個同學必須先找秘書初試,然后到部門主管去復制。最后到經理處去面試,而且不同意插隊。因為四名同學的專業背景不同,所以沒人在三個階段的面試時間也不一樣,例如以下表。
這四名同學約定他們所有面試完畢以后一起離開公司,問他們最快用多長時間完畢面試?
?
這里給出求解的代碼
?
!三階段面試模型;
model:
sets:students;!學生集三階段面試模型;phases;!階段集;sp(students,phases):t,x;ss(students,students)|&1 #lt# &2:y;
endsets
data:students=s1..s4;phases=p1..p3;t=13 15 2010 20 1820 16 108 10 15;
enddatans=@size(students);!學生數;np=@size(phases);!階段數!單個學生面試時間先后順序的約束;@for(sp(I,J)|J#LT#np:x(I,J)+t(I,J)<=x(I,J+1));!學生間的面試先后次序保持不變的約束;@for(ss(I,K):@for(phases(J):x(I,J)+t(I,J)-x(K,J)<=200*y(I,K);x(K,J)+t(K,J)-x(I,J)<=200*(1-y(I,K));));min=TMAX;@for(students(I):x(I,3)+t(I,3)<=TMAX);!把Y定義0-1變量;!把Y定義0-1變量;@for(ss:@bin(y));
end?以后假設遇到對應的更好的模型是,我會有選擇的加上的。
?
?
?
?
?
















)





)

)
