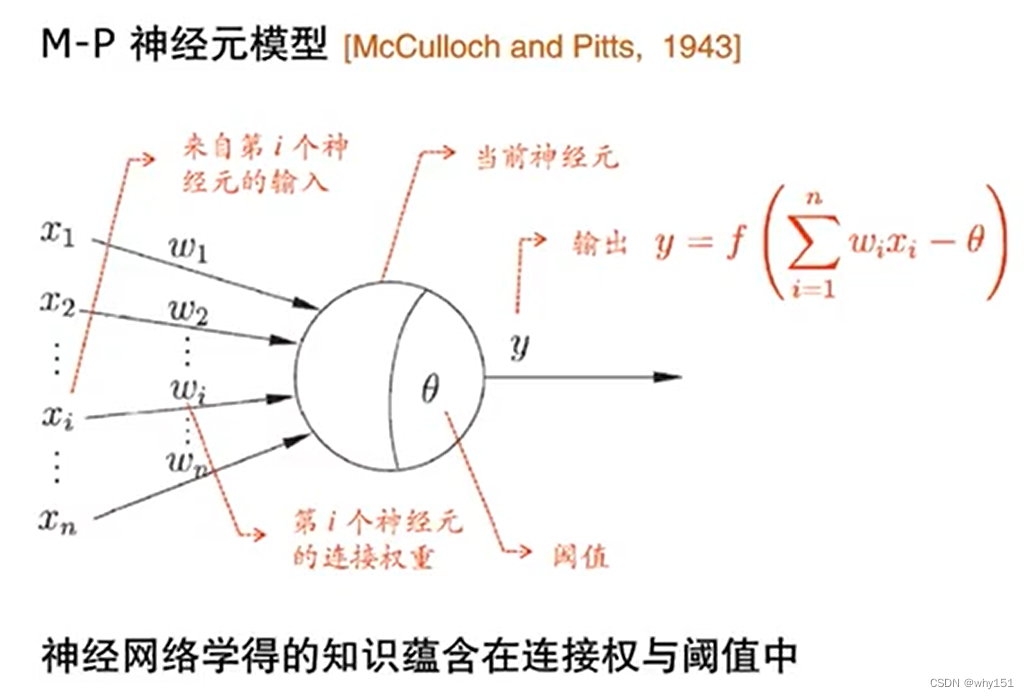
神經元模型

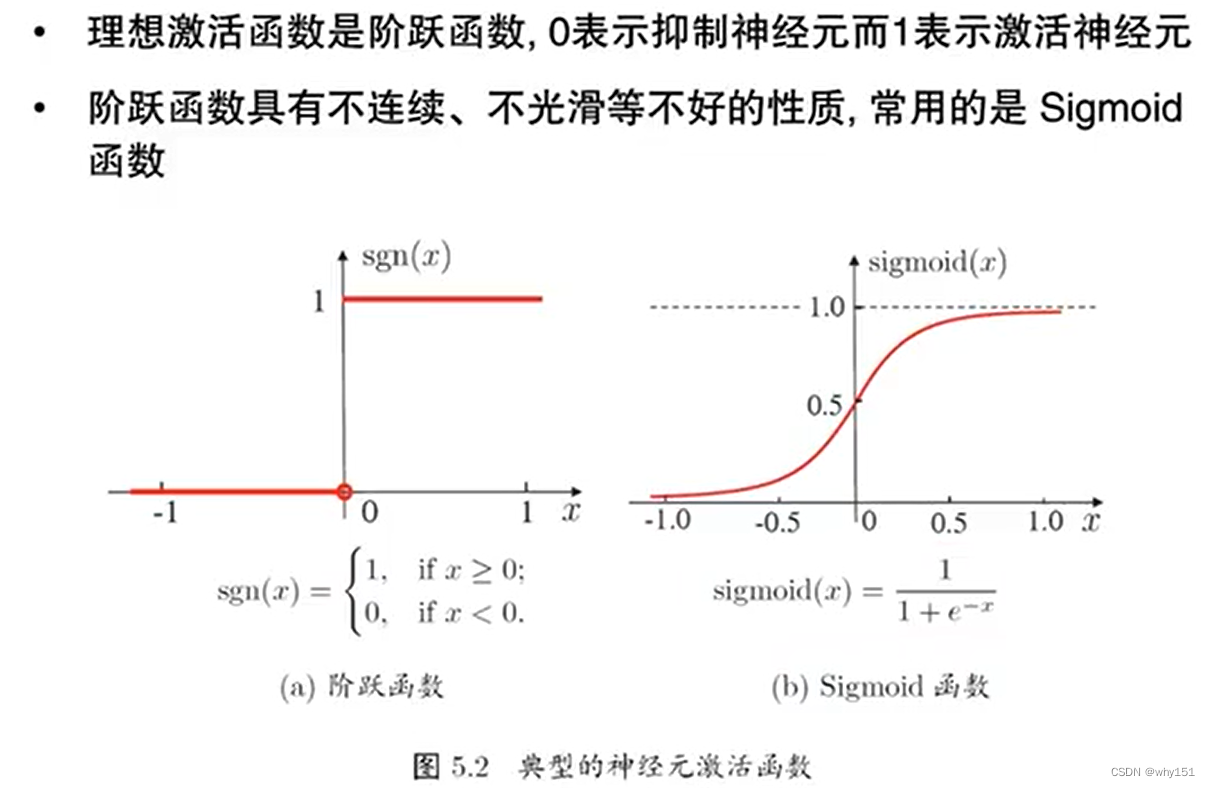
上述定義的簡單單元即為神經元模型。

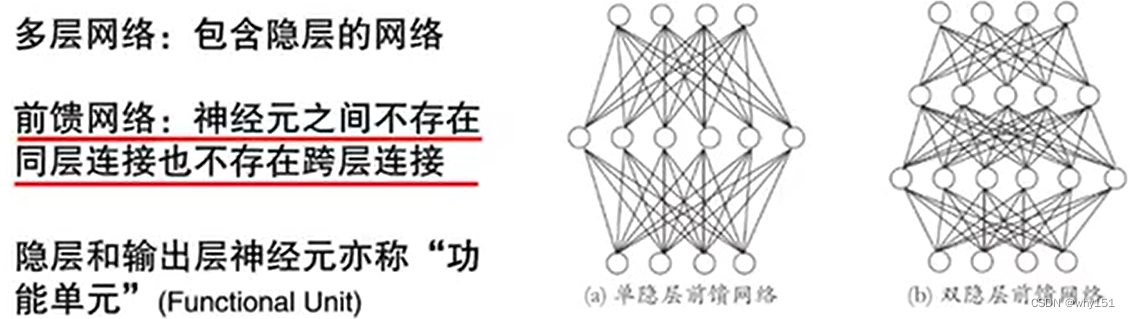
多層網絡

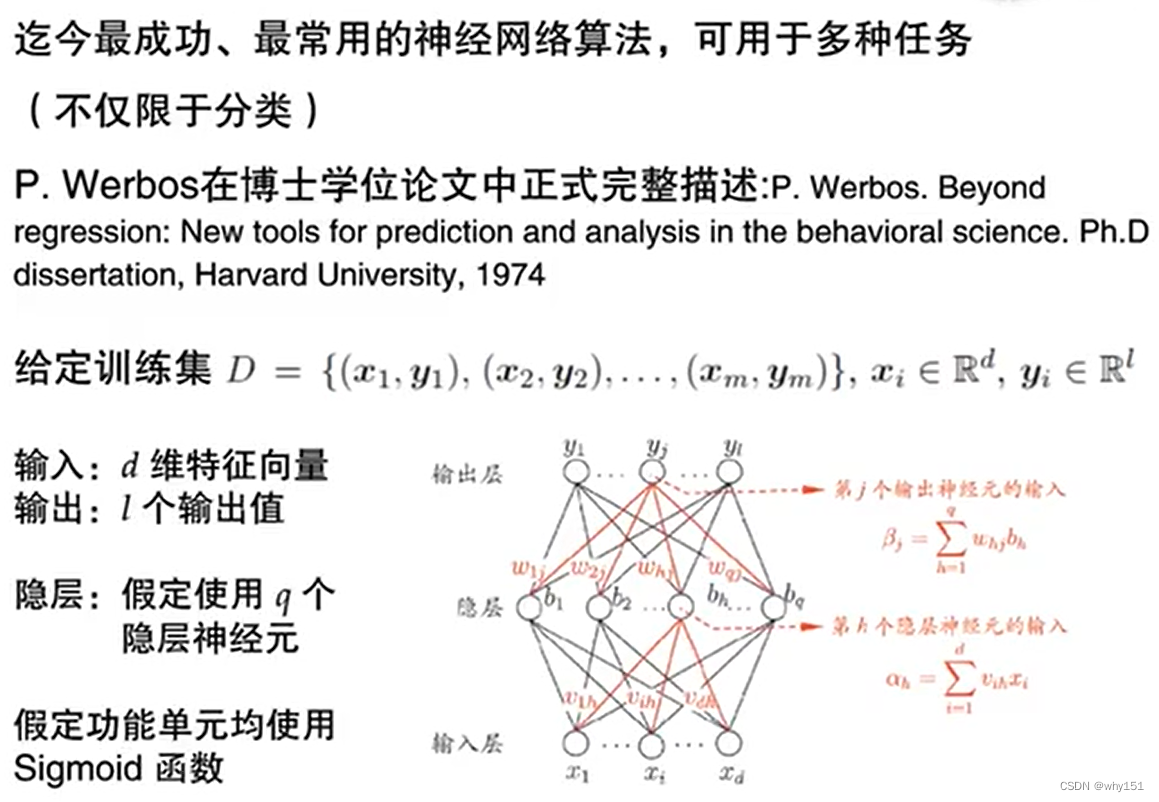
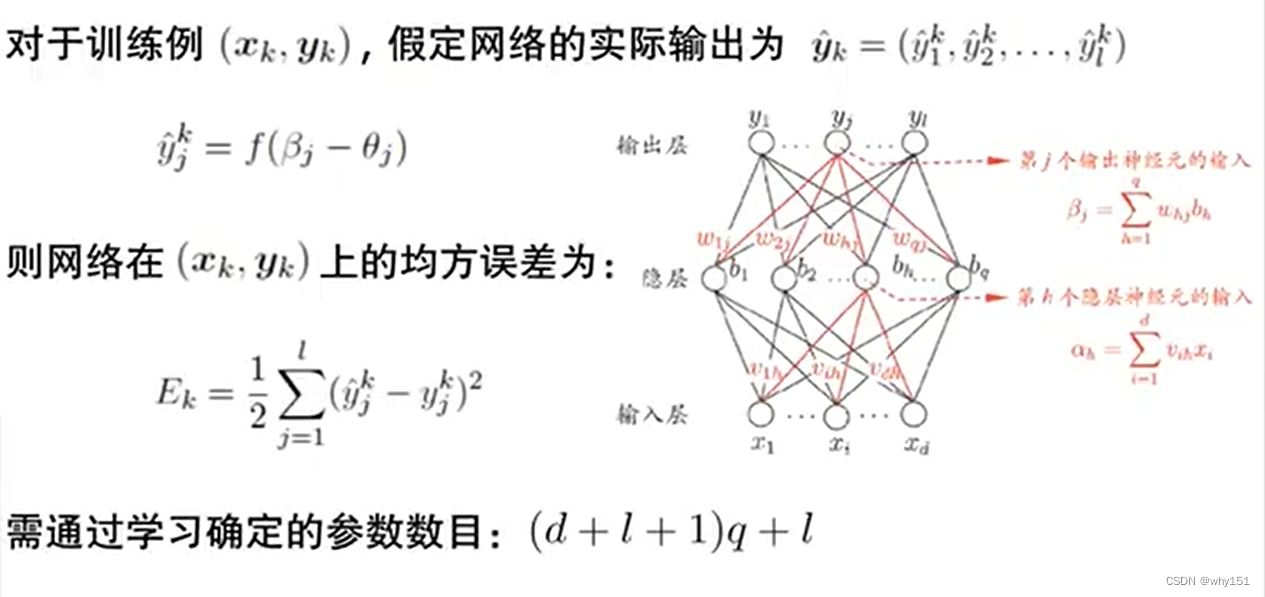
誤差逆傳播算法

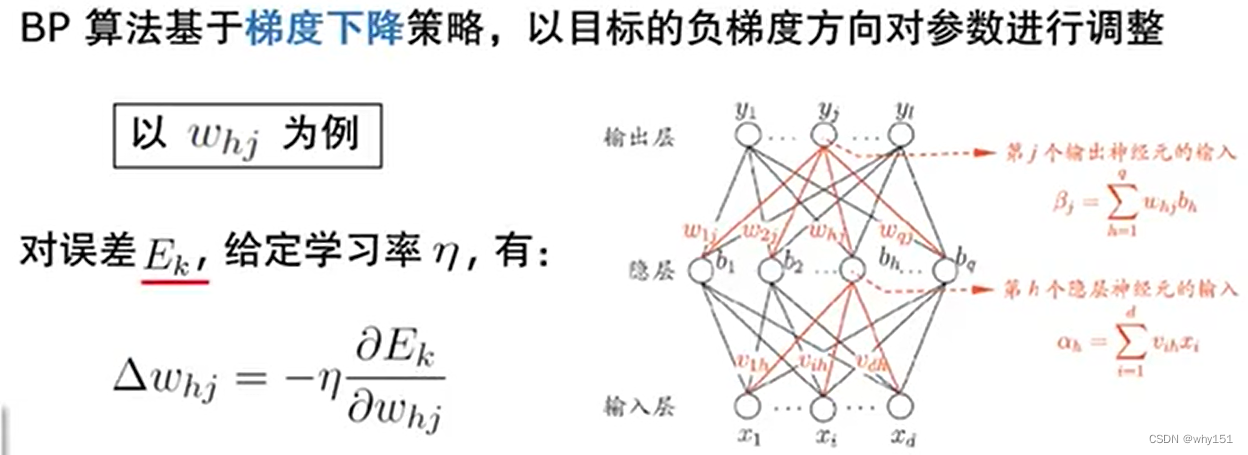
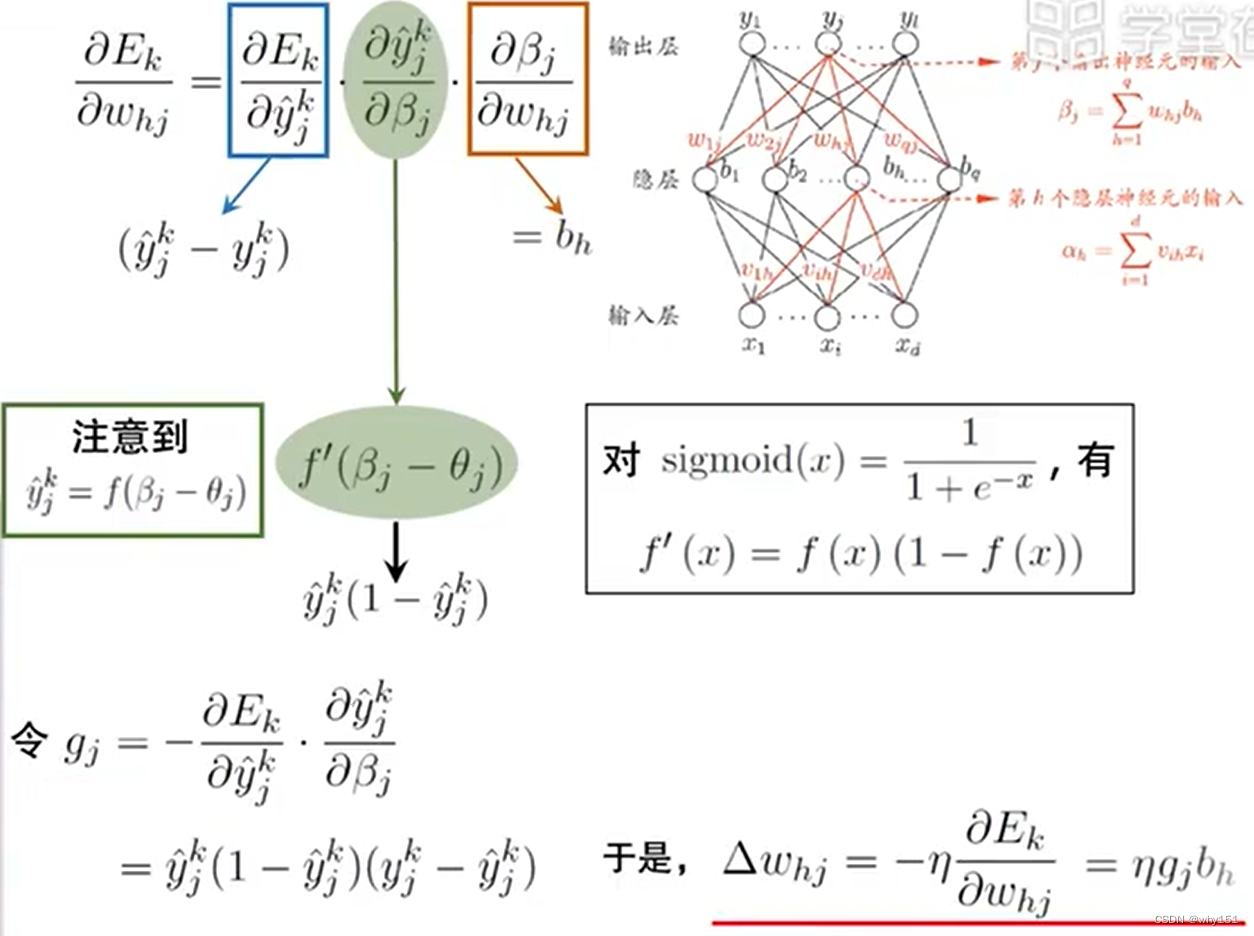
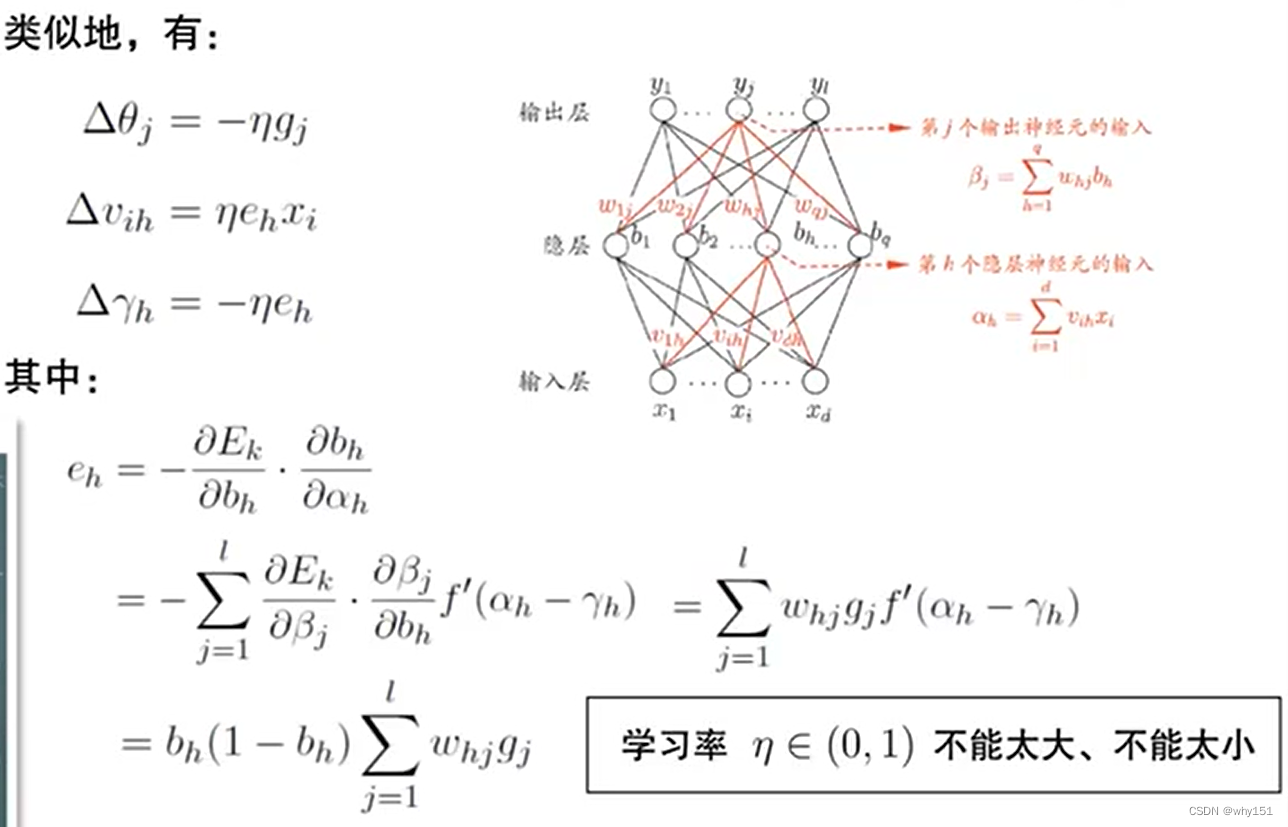
• 標準BP算法：參數更新非常頻繁，可能出現抵消現象。
• 積累BP算法：下降到一定程度上，進行下一步會非常緩慢。

過擬合

• 早停：劃分訓練集和驗證集，若訓練集誤差降低而驗證集升高則停止訓練。
• 正則化：在誤差目標函數中加入一個用于描述網絡復雜度的部分，$E=\lambda \frac{1}{m}{\sum }_{k=1}^m{E}_k+(1?\lambda ){\sum }_i{w}_i^2$

全局最小與局部極小

• 局部極小解：是參數空間的某個點，其鄰域點的誤差函數值均不小于該點的誤差函數值，可能存在多個。
• 全局極小解：是指參數空間中所有點的誤差函數值均不小于該點的誤差函數值，只存在一個。

如何跳出局部極小值點？

• 以多組不同參數值初始化多個神經網絡，取誤差最小的解。
• 使用模擬退火，在每一步都有一定概率接受比當前解更差的算法。
• 使用隨機梯度下，即便陷入局部極小點，它計算出來的梯度仍然可能不為0。