原文鏈接：

拓端數據科技 / Welcome to tecdat?tecdat.cn

在保險業中，由于分散投資，通常會在合法的大型投資組合中提及大數定律。在一定時期內，損失“可預測”。當然，在標準的統計假設下，即有限的期望值和獨立性。由于在保險業中，災難通常很少發生，而且代價非常高昂，精算師可能有興趣對少量事件的發生進行建模。背后的定理有時也被稱為小數定律。

泊松分布

所謂的泊松分布（請參閱http://en.wikipedia.org/…）由SiméonPoisson于1837年進行了介紹。亞伯拉罕·德·莫伊夫（Abraham De Moivre）于1711年在De Mensura Sortis seu對其進行了定義。

讓

表示一個計數隨機變量，然后它是服從泊松分布，如果有

這

De Moivre從二項式分布的近似值獲得了該分布。回想一下，二項式分布是精算科學中的標準分布，例如，用來模擬

被保險人死亡人數 。如果單個死亡概率相同，例如

，并且如果死亡是獨立事件，則

而如果

和

，然后

再次，這是一個漸近定理，當我們有很多觀察值時（

）成立，它也成立，而且出現的可能性應該非常小（因為

），這就是為什么要使用術語“ 小數”的原因。SiméonPoisson對數學近似值不感興趣：他的主要觀點是針對他正在處理的數據獲得具有良好擬合優度的分布。

小數定律

與Poisson分布有關的主要定理的啟發式如下：

表示iid隨機變量采用值

（一般情況下，一個分量可以是時間，另一分量可以是感興趣的上部區域，其中某些隨機過程是可能）。讓

。如果

作為假設

（或

更具體地假設），則

表示事件的（隨機變量表征）計數

，則

可以通過帶有參數的泊松分布來近似

。
啟發式方法是，如果考慮大量觀察值，并且計算給定（小）區域中有多少觀察值，則此類觀察值的數量就是泊松分布。

1. 
   n=1000
8. 
   polygon(c(u,rev(u)),c(v,rev(-v)),col="yellow",border=NA)
9. 
   I=(X^2+Y^2)<1
10. 
    points(X[I],Y[I],cex=.6,pch=19,col="red")

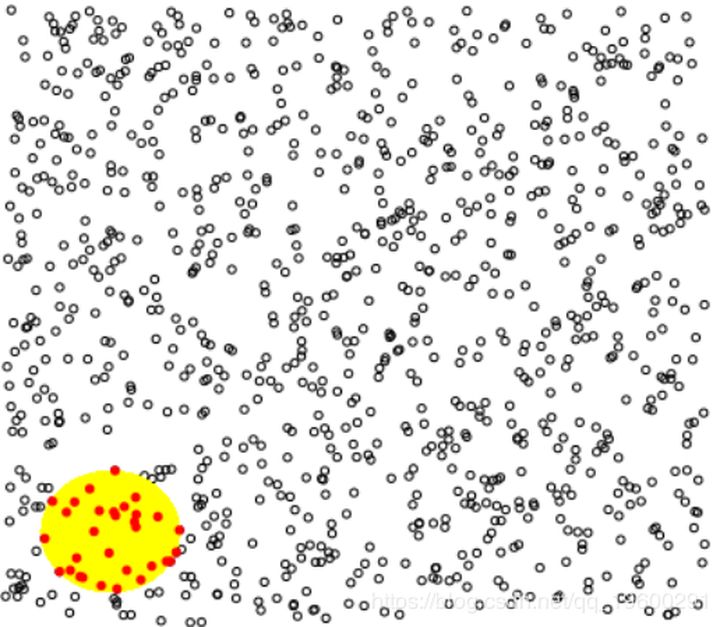
如果我們進行一些模擬

1. 
   > n=1000
2. 
   > ns=100000
3. 
   > N=rep(NA,ns)
4. 
   >
5. 
   +
6. 
   +
7. 
   +
8. 
   +
9. 
   +
10. 
    >
11. 
    > mean(N)
12. 
    [1] 31.41257

泊松分布的參數是黃色圓盤的面積，即正方形的面積，即

2. 
   > lines(0:60-.5,dpois(0:60,lambda),type="b",col="red")

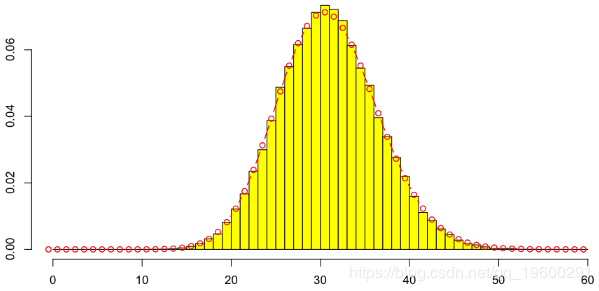
為了獲得與保險模型有關的解釋，讓我們

在再保險合同中表示上層，即

某些可扣除額

。讓我們

來表示個人損失。然后，可以使用泊松分布對到達該上層的索賠的數量進行建模。更準確地說，如果自付額

變得非常大（和

），我們將獲得極值理論中的閾值點以上模型：如果

有一個泊松分布，并在有條件的

，

是獨立同分布的廣義帕累托隨機變量，然后

具有廣義的極值分布。因此，超出模型（針對罕見事件）與泊松過程密切相關。

泊松過程

如上所述，當事件以某種方式隨機且獨立地隨時間發生時，就會出現泊松分布。然后很自然地研究兩次事件之間的時間（或在保險范圍內兩次索賠）。

泊松分布和索賠發生

既不是SiméonPoisson也不是De Moivre，而是Ladislaus Von Bortkiewicz首先提到了Poisson分布是小數定律。1898年，他研究了1875年至1894年間被馬踢倒殺死的士兵的人數，其中有200個兵團。

他確實獲得了以下分布（此處，泊松分布的參數為0.61，即每年的平均死亡人數）

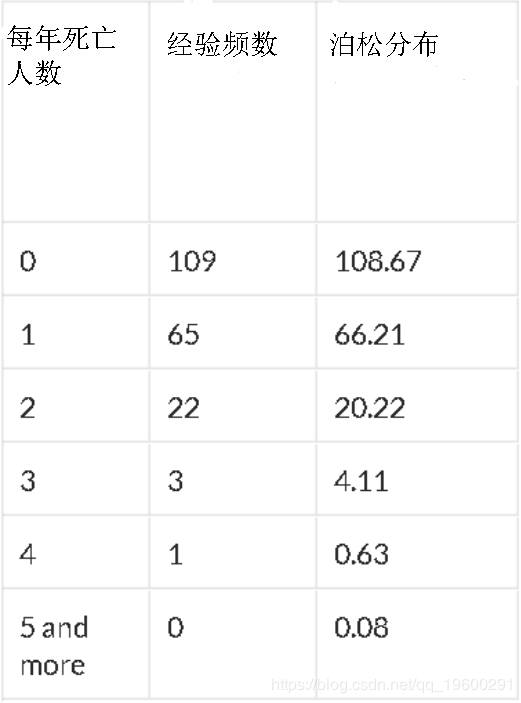
在很多情況下，泊松分布都非常適合。例如，如果我們考慮1850年后在佛羅里達州的颶風數量，

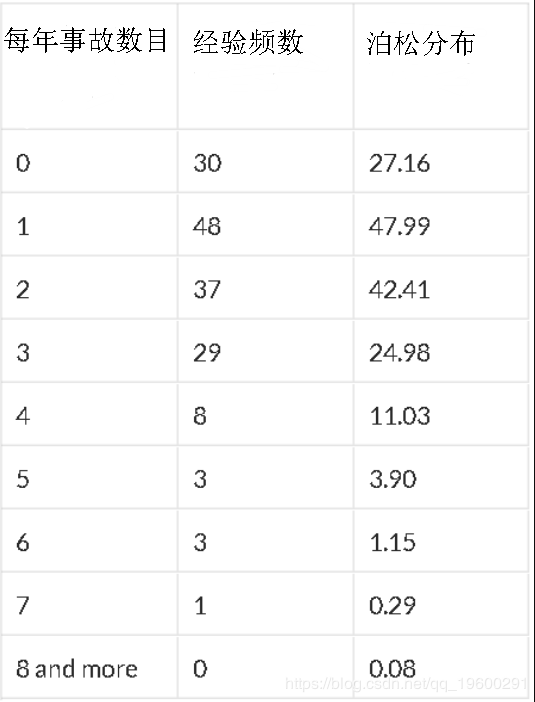
泊松分布和回歸期

返回期是由Emil Gumbel在水文學中介紹的，用于鏈接概率和持續時間。十年事件的發生概率為1/10。那么10是發生之前的平均等待時間。這并不意味著該事件不會在10年之前發生，或者必須在10年之前發生。考慮一個返回期

（以年為單位），則每年不出現的概率為

。

則

多年未發生的概率為

。通常用下表來總結此屬性，

上表中的對角線非常有趣。似乎在某種程度上趨向極限值（此處為63.2％）。在n年內觀察到的事件數量具有二項式分布，其概率為

，將收斂到參數為1的泊松分布。那么

，沒有災難的概率為，等于0.632。

稀有概率與泊松分布

計算稀有事件的概率時，泊松分布不斷出現。例如，在50年的時間里，至少有一次在核電廠發生事故的可能性。假設在反應堆中發生事故的年概率

很小，例如0.05％。進一步假設反應堆在時間上相互獨立。在50年內發生超過80個反應堆的事件的概率是

當然，線性近似是不正確的

另一方面

1. 
   >
2. 
   >
3. 
   [1] 0.1812733
4. 
   >
5. 
   [1] 0.1812692

這是具有參數為的泊松分布

時為零 的概率 。我們在這里清楚地看到近似在風險管理中的應用。

解決這個問題的另一種方法是基于以下思想：鑒于在對全球450座反應堆進行的45年觀察中（，觀察到了三起重大事故，包括“三哩島”（1979年）和“福島”（2011年），即兩次事故之間的平均時間估計為16年。對于單個反應堆，我們可假設事件發生之前等待的平均時間是16年的450倍，即7200年。或者，一個反應堆在一年內發生一次事件的概率是7200以上的事件之一（這是“返還期”概念背后的想法）。如果我們假設事故的到來是隨機且彼此獨立發生的（如上定義），則在50年內觀察到的重大事故數量遵循參數為50 /（7200/80）的泊松分布。也，

即

1. 
   >
2. 
   [1] 0.4262466

---

參考文獻
1.R語言泊松Poisson回歸模型分析案例
2.R語言進行數值模擬：模擬泊松回歸模型
3.r語言泊松回歸分析
4.R語言對布豐投針（蒲豐投針）實驗進行模擬和動態可視化
5.用R語言模擬混合制排隊隨機服務排隊系統
6.GARCH（1,1），MA以及歷史模擬法的VaR比較
7.R語言做復雜金融產品的幾何布朗運動的模擬
8.R語言進行數值模擬：模擬泊松回歸模型
9.R語言對巨災風險下的再保險合同定價研究案例：廣義線性模型和帕累托分布Pareto distributions