(建議閱讀全文)
預備知識 萬有引力, 彈簧振子受迫運動的簡單數值計算 下面我們來用一種極其簡單的算法對單個天體在中心天體的萬有引力作用下的運動進行數值計算. 事實上該問題存在解析解(見開普勒三定律), 所以以下的算法只是用于演示數值解常微分方程的大致原理. 這種方法可以輕易地拓展到多個天體的情況, 而多體情況沒有一般的解析解. 一種效率更高的常見常微分方程數值算法可參考 “四階龍格庫塔法”. 直角坐標系中, 設中心天體質量為
其中
用
假設已知初值條件
2.設經過一段極微小的時間步長
3.把
% 參數設定
GM = 1; % 萬有引力常數乘以中心天體質量
x0 = 1; y0 = 0; % 初始位置
vx0 = 0; vy0 = 0.7; % 初始速度
T = 4; Nstep = 4000; % 總時間和步數
dt = T/Nstep; % 步長% 矩陣預賦值
x = nan(Nstep,1); y = x;
x1 = x; y1 = x;
x2 = x; y2 = x;% 初始位置,速度,加速度
x(1) = x0; y(1) = y0; % 初位置
x1(1) = vx0; y1(1) = vy0; % 初速度
x2(1) = -GM*x(1)/(x(1)^2+y(1)^2)^(3/2); % 代入方程得到 x''(0)
y2(1) = -GM*y(1)/(x(1)^2+y(1)^2)^(3/2); % 代入方程得到 y''(0)% 迭代循環
for ii = 2:Nstepx(ii) = x(ii-1)+x1(ii-1)*dt; % x的微分y(ii) = y(ii-1)+y1(ii-1)*dt; % y的微分x1(ii) = x1(ii-1)+x2(ii-1)*dt; % x' 的微分y1(ii) = y1(ii-1)+y2(ii-1)*dt; % y' 的微分x2(ii) = -GM*x(ii)/(x(ii)^2+y(ii)^2)^(3/2); % 代入微分方程求出 x''y2(ii) = -GM*y(ii)/(x(ii)^2+y(ii)^2)^(3/2); % 代入微分方程求出 y''
end% 畫圖
plot(x,y); % 畫行星軌道
axis equal; % xy坐標長度一致
hold on; % 繼續畫圖
scatter(0,0); % 標出中心天體程序運行結果如圖 1 所示. 注意行星軌道并不是一個閉合的橢圓, 這是由于這種算法誤差較大, 為了減小誤差, 可以增加程序中 Nstep 的值. 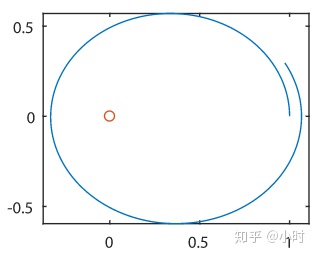



![php cpu mac,PHP 獲得計算機的唯一標識[CPU,網卡 MAC地址]](http://pic.xiahunao.cn/php cpu mac,PHP 獲得計算機的唯一標識[CPU,網卡 MAC地址])








![二分+樹的直徑 [Sdoi2011]消防](http://pic.xiahunao.cn/二分+樹的直徑 [Sdoi2011]消防)






