- 論文作者簡介
本論文第一作者Matt J. Kusner是牛津大學的副教授,致力于設計適應現實世界問題需求的新機器學習模型(例如,fair algorithms, discrete generative models, document distances, privacy, dataset compression, budgeted learning, and Bayesian optimization)。
- 論文摘要
論文中作者提出了一個度量文本文檔之間距離的新指標,即詞移距離WMD(Word Mover's Distance)。該成果基于Mikolov等人提出的詞嵌入(word embeddings),一種語義上有意義的詞匯表征。具體來說,將每個單詞標記編碼為某個向量,該向量表示為某種“單詞”空間中的一個點(該空間的維數遠遠小于詞匯表的大小|V|),每個維度都會編碼某個含義。WMD距離衡量的是兩個文本文檔之間的差異性,即一篇文檔的詞匯需要對應到另一篇文檔的某一個相近詞匯,取該過程中所生成距離的最小值作為文檔距離。該距離度量可以視為Earth Mover's Distance的一個特例。作者在8個現實世界的文檔分類數據集上,與當時7個state-of-the-art的基準算法相比較,WMD度量取得了前所未有的較低的K最近鄰文檔分類錯誤率。
- 論文內容介紹
準確地表示兩個文檔之間的距離在文檔檢索、新聞分類和聚類、歌曲識別和多語言文檔匹配中具有廣泛的應用。早先通過詞袋模型BOW(bag of words)或詞頻-逆向文件頻率TF-IDF(term frequency-inverse document frequency)表示文檔的方式,由于它們頻繁的接近正交的特性,故不適用于文檔距離。這些表示方式的另一個顯著缺點是他們沒有捕獲到單詞之間的距離。作者利用Mikolov等人提出的word2vec模型構建了新的文檔距離度量指標Word Mover's Distance (WMD),將文本文檔表示為詞嵌入向量的加權點云,每個詞嵌入向量對應高維空間中的一個點。兩篇文本文檔A和B之間的距離是一個最小累積距離,該距離是來自文檔A的單詞需要travel來精確匹配文檔B的點云。見下方新度量指標的略圖。

作者還比較了幾個下限方法,這些下限方法可以用作近似計算或者修剪掉被證明不在一個查詢的k個最近鄰中的文檔。WMD距離具有幾個有趣的特性:(1) 沒有超參數,易于理解和使用; (2)高度可解釋的,兩個文檔之間的距離可以分解并解釋為少數幾個單詞之間的稀疏距離;(3)它自然地融入了word2vec空間中的編碼知識并獲得高檢索準確率。作者是首次將高質量的詞嵌入和EMD檢索算法關聯起來進行文檔距離研究的。
- 詞嵌入向量(word embedding vector)
比如,針對300維的詞嵌入向量,每個維度表示某個特定的含義。詞匯表中所有詞匯構成的詞嵌入矩陣(word embedding matrix)如下圖所示(圖中的每一列表示該詞匯對應的詞嵌入向量,例如單詞man表示的詞嵌入向量為
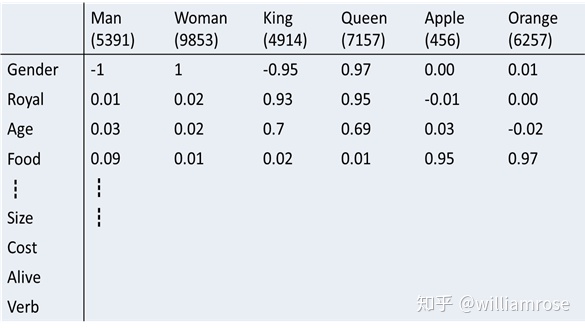
- Word Mover's Distance
nBOW:假設有n個單詞的詞匯表的word2vec嵌入矩陣
Word travel cost:我們的目標是將每個單詞對(例如,President and Obama)之間的語義相似度包含進文檔距離度量中。單詞
Document distance:兩個詞之間的“travel cost”是一個自然的構建塊用以創建兩個文檔之間的距離。令
Transportation problem:在給定約束條件下,將文檔
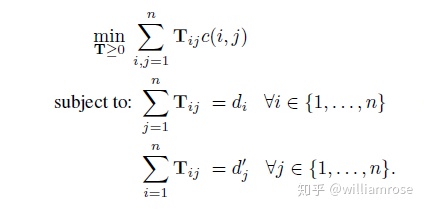
上述優化問題可以看做是earth mover's distance metric(EMD)的一個特例。
Visualization:考慮WMD度量文檔距離的一個例子,

- Fast Distance Computation
由于解決WMD優化問題的最佳平均時間復雜度為
下限方法1(Word centroid distance):質心距離
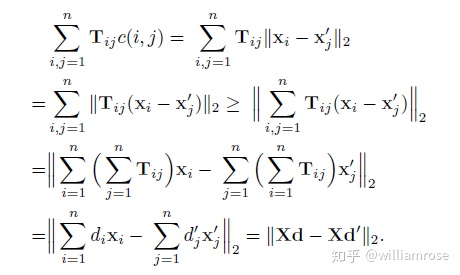
note:矩陣向量乘法的第二種形式
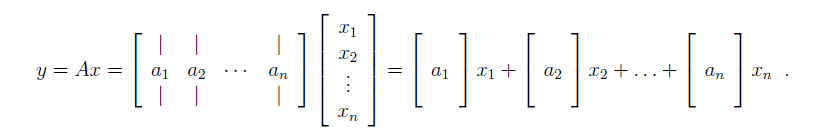
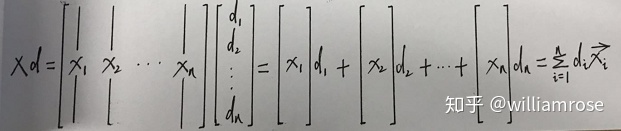
將該距離稱為Word Centroid Distance(WCD),每個文檔由其加權平均詞向量表示。該下限計算方法只需要通過幾個矩陣運算便可得出,時間復雜度也只有O(dp)
下限方法2(Relaxed word moving distance):由于WCD計算出的下限比較寬松,通過松弛WMD優化問題并分別移除兩個約束條件中的一個,我們可以得到更嚴格的界限。如果只移除第二個約束條件,優化問題就變成了,
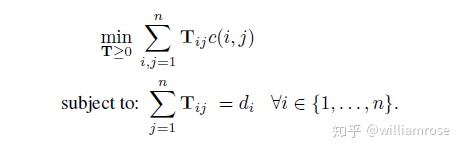
這個松弛問題一定會產生WMD距離的一個下限(lower-bound),一個明顯的事實是每個WMD的解決方案(滿足兩個約束條件),一定仍然是移除一個約束條件的松弛問題的一個可行解決方案。令兩個松弛解決方案分別是
Prefetch and prune:我們使用兩個下限來大幅減少我們需要進行的WMD距離計算量,以便找到一個查詢文檔的k個最近鄰。首先將所有文檔按照它們到查詢文檔的WCD距離(該距離計算成本廉價)進行升序排列,然后計算查詢文檔到這些文檔中前k個文檔的精確WMD距離。接下來遍歷剩余的其它文檔。對于余下的每篇文檔我們首先檢查RWMD下限是否超過當前第k個最近文檔的距離,如果是這樣我們就將其修剪掉。否則的話就計算WMD距離并在必要時更新第k個最近鄰。由于RWMD近似非常嚴格,它允許我們在一些數據集上修剪掉高達95%的文檔數。
- 結果
作者在八個基準文檔分類任務上以kNN分類的形式評估了WMD距離(word mover’s distance)。
1、8個監督學習范疇的公開文檔數據集
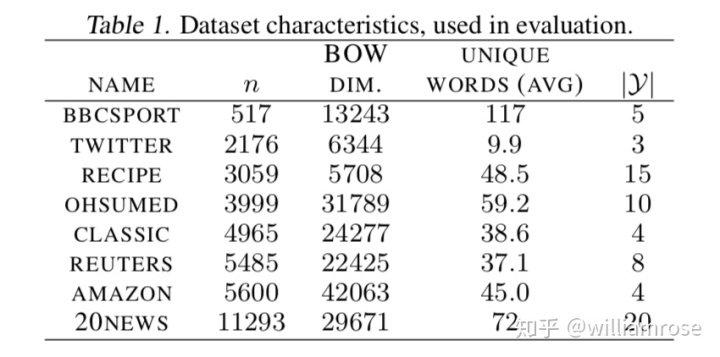
2、用于與WMD距離相比較的表示文檔的7個基準方法
對于每個基準方法,我們使用歐氏距離進行kNN分類。
bag-of-words (BOW), TFIDF(term frequency-inverse document frequency), BM25 Okapi, LSI(Latent Semantic Indexing), LDA(Latent Dirichlet Allocation), mSDA(Marginalized Stacked Denoising Autoencoder), CCG(Componential Counting Grid)
3、文檔分類結果
在除了兩個(BBCSPORT,OHSUMED)之外的所有數據集上,WMD取得了最低的測試誤差。
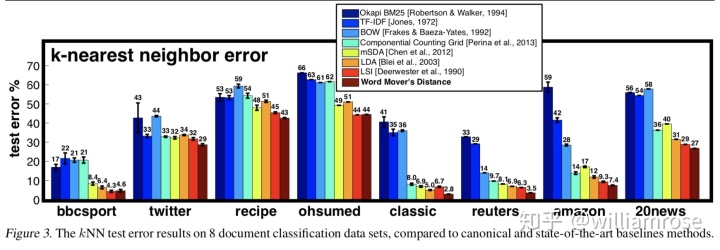
4、Lower Bounds and Pruning
最后,作者評估了在m的不同取值下prefetch和prune算法的精確和近似版本的加速性能和準確性。所有加速都是相對于詳盡的WMD度量所需時間(圖的最上方)而報告的,并且在4個核心上并行運行。(8 cores for 20NEWS) of an Intel L5520 CPU with 2.27Ghz clock frequency.首先,我們注意到在所有情況下,通過prefetching增加的錯誤相對較小,而可以獲得可觀的速度提升。
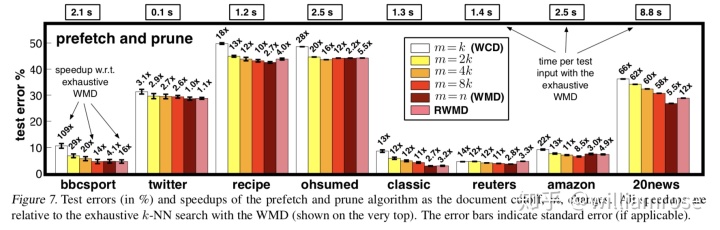
從圖中可以觀察到,誤差在m = k和m = 2k之間下降最多,對于時間敏感的應用來說,這可能會產生一個介于準確率和檢索時間之間的最佳點(sweet spot)。如前所述,使用RWMD直接導致令人印象深刻的低錯誤率,并且在所有數據集上的平均檢索時間低于1秒。
- 結論
WMD度量在所有數據集上的錯誤率如此之低,我們將其歸因于其利用了word2vec詞嵌入向量高效表征詞匯的能力。
- 參考文獻:
【1】Matt J. Kusner, From Word Embeddings To Document Distances
【2】Mikolov, T., Chen, K., Corrado, G., and Dean, J. Efficient estimation of word representations in vector space. In Proceedsings of Workshop at ICLR, 2013a.
【3】Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., and Dean, J. Distributed representations of words and phrases and their compositionality. In NIPS, pp. 3111– 3119, 2013b.
Word2Vec Tutorial - The Skip-Gram Model
吳恩達、深度學習第五門課程-序列模型(sequence models)、網易云課堂












C語言版(轉))


)



)