文章目錄
- 11.1 C++ STL
- 11.2 數組
- 448. 找到所有數組中消失的數字(簡單)
- 48. 旋轉圖像(中等)
- 74. 搜索二維矩陣(中等)
- 240. 搜索二維矩陣 II(中等)
- 769. 最多能完成排序的塊(中等)
- 768. 最多能完成排序的塊 II(困難)
- 11.3 棧和隊列
- 232. 用棧實現隊列(簡單)
- 155. 最小棧(中等)
- 20. 有效的括號(簡單)
- 11.4 單調棧
- 739. 每日溫度(中等)
- 11.5 優先隊列
- 23. 合并 K 個升序鏈表(困難)
- 218. 天際線問題(困難)
- 11.6 雙端隊列
- 239. 滑動窗口最大值(困難)
- 11.7 哈希表
- 1. 兩數之和(簡單)
- 128. 最長連續序列(中等)
- 149. 直線上最多的點數(困難)
- 11.8 多重集合和映射
- 332. 重新安排行程(困難)
- 11.9 前綴和與積分圖
- 303. 區域和檢索 - 數組不可變(簡單)
- 304. 二維區域和檢索 - 矩陣不可變(中等)
- 560. 和為 K 的子數組(中等)
- 11.10 練習
- 566. 重塑矩陣(簡單)
- 225. 用隊列實現棧(簡單)
- 503. 下一個更大元素 II(中等)
- 217. 存在重復元素(簡單)
- 697. 數組的度(簡單)
- 594. 最長和諧子序列(簡單)
- 287 . 尋找重復數(中等)
- 313. 超級丑數
- 870 . 優勢洗牌
- 307 . 區域和檢索 - 數組可修改
11.1 C++ STL
C++ 提供的數據結構包括:
-
Sequence Containers:維持順序的容器。
- vector:動態數組,用于 O(1) 的隨機讀取。因為大部分算法的時間復雜度都會大于 O(n) ,因此我們經常新建 vector 來存儲各種數據或中間變量。
- list:雙向鏈表,也可以當作 stack 和 queue 來使用。由于 LeetCode 的題目多用 Node 來表示鏈表,且鏈表不支持快速隨機讀取,因此很少用到該數據結構。 一個例外是經典的 LRU 問題,需要利用鏈表的特性來解決。
- deque:雙端隊列,既支持 O(1) 的隨機讀取,又支持 O(1) 時間的頭部增刪和尾部增刪,不過有一定的額外開銷。
- array:固定大小的數組,一般不使用。
- forward_list:單向鏈表,一般不使用。
-
Container Adaptors:基于其他容器實現的數據結構。
- stack:后入先出(LIFO) 的數據結構,默認基于 deque 實現,stack常用于深度優先搜索、字符串匹配問題以及單調棧問題。
- queue:先入先出(FIFO) 的數據結構,默認基于 deque 實現,queue 常用于廣度優先搜索。
- priority_queue:最大值先出的數據結構,默認基于 vector 是實現堆結構。它可以在 O(n logn) 的時間排序數組, O(logn) 的時間插入任意值,O(1) 的時間獲得最大值, O(logn) 的時間刪除最大值。 priority_queue 常用于維護數據結構并快速獲取最大或最小值。
-
Associative Containers:實現了排好序的數據結構。
-
set:有序集合,元素不可以重復,底層實現默認為紅黑樹,即一種特殊的二叉查找樹(BST)。它可以在 O(nlogn) 的時間排序數組,O(logn) 的時間插入、刪除、查找任意值,O(logn) 的時間獲得最小或最大值。
這里注意,set 和 priority_queue 都可以用于維護數據結構并快速獲取最大最小值,但是它們的時間復雜度和功能略有區別。比如, priority_queue 默認不支持刪除任意值,而 set 獲得最大或最小值的時間復雜度略高。
-
multiset:支持重復元素的 set。
-
map: 有序映射或有序表,在 set 的基礎上加上映射關系,可以對每個元素 key 存一個值 value。
-
multimap:支持重復元素的 map。
-
-
Unordered Associative Containers:對每個 Associative Containers 實現了哈希版本。
- unordered_set :哈希集合,可以在 O(1) 的時間快速插入、查找、刪除元素,常用于快速查詢一個元素是否在這個容器內。
- unordered_multiset:支持重復元素的 unordered_set 。
- unordered_map:哈希映射或哈希表,在 unordered_set 的基礎上加上映射關系,可以對每一個元素 key 存一個值 value。在某些情況下,如果 key 的范圍已知且較小,我們也可以用 vector 代替 unordered_map,用位置表示 key,每個位置的值表示 value。
- unordered_multimap:支持重復元素的 unordered_map。
11.2 數組
448. 找到所有數組中消失的數字(簡單)



思路及代碼: 448. 找到所有數組中消失的數字
48. 旋轉圖像(中等)

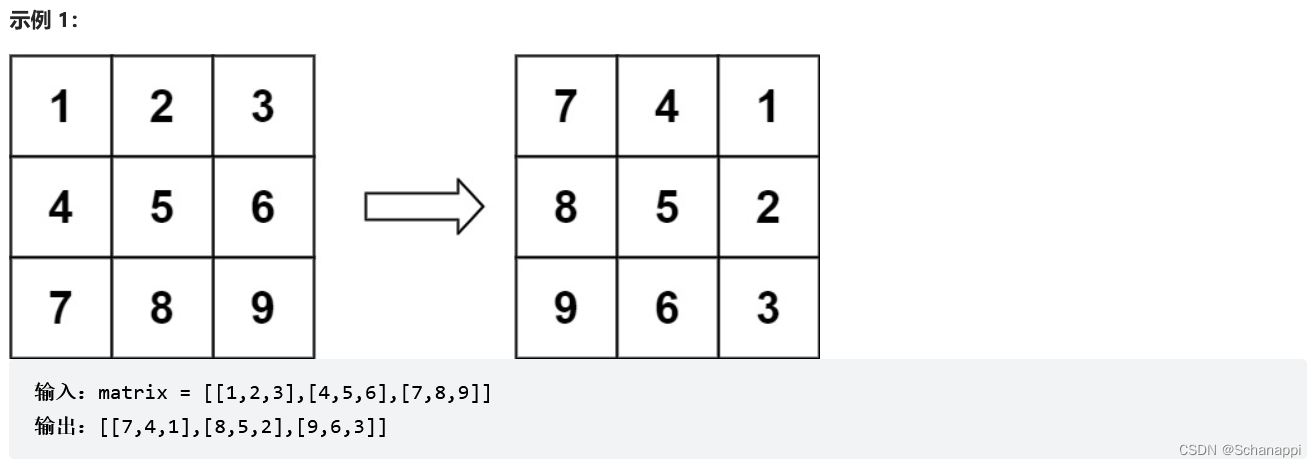
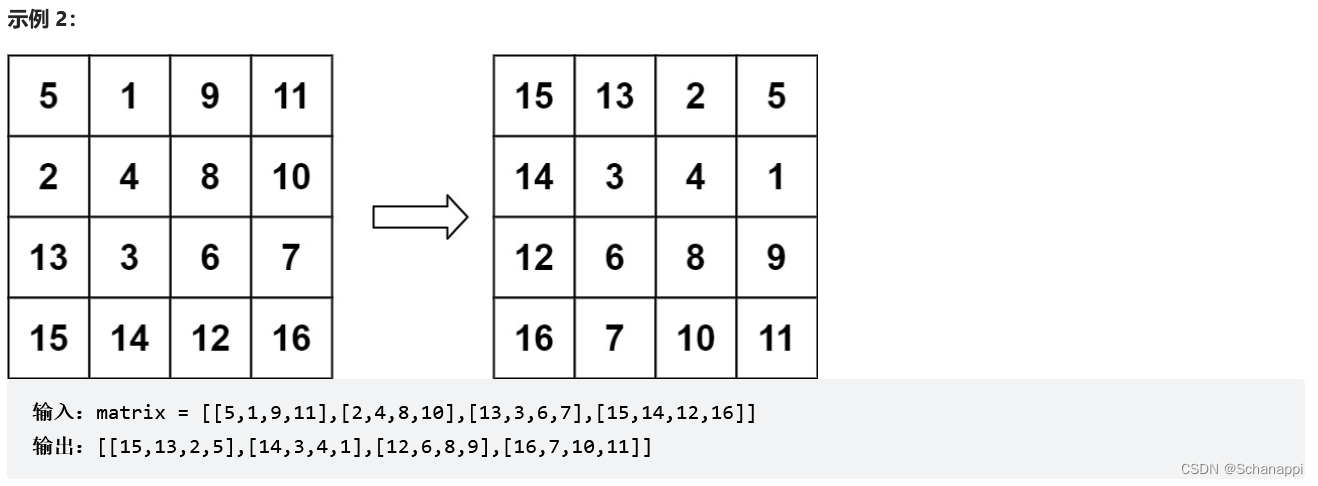

思路及代碼: 48. 旋轉圖像
74. 搜索二維矩陣(中等)

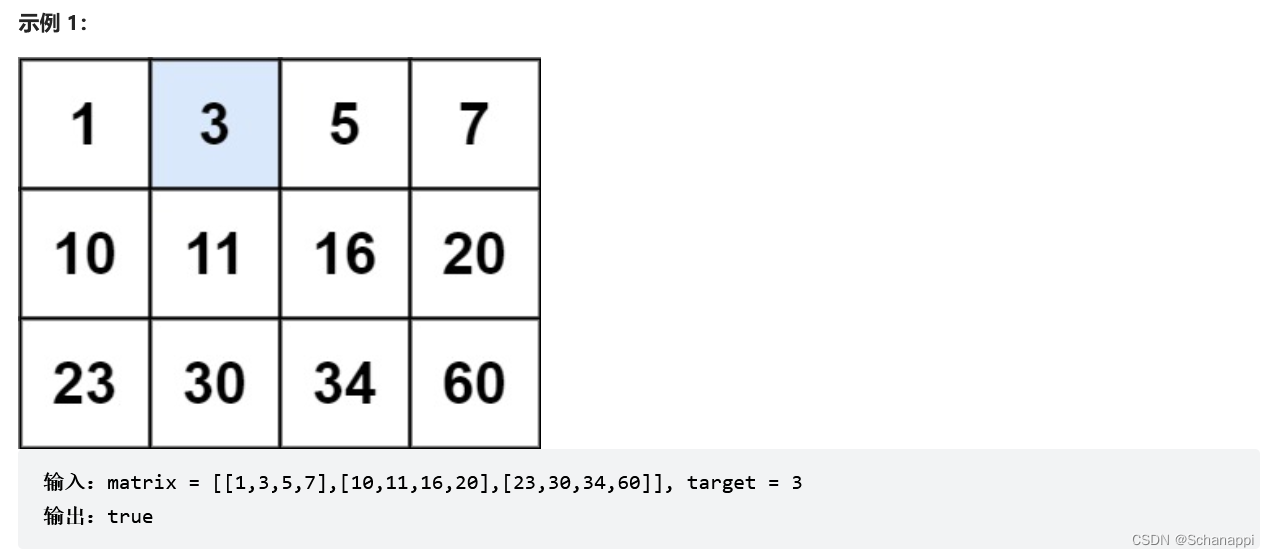
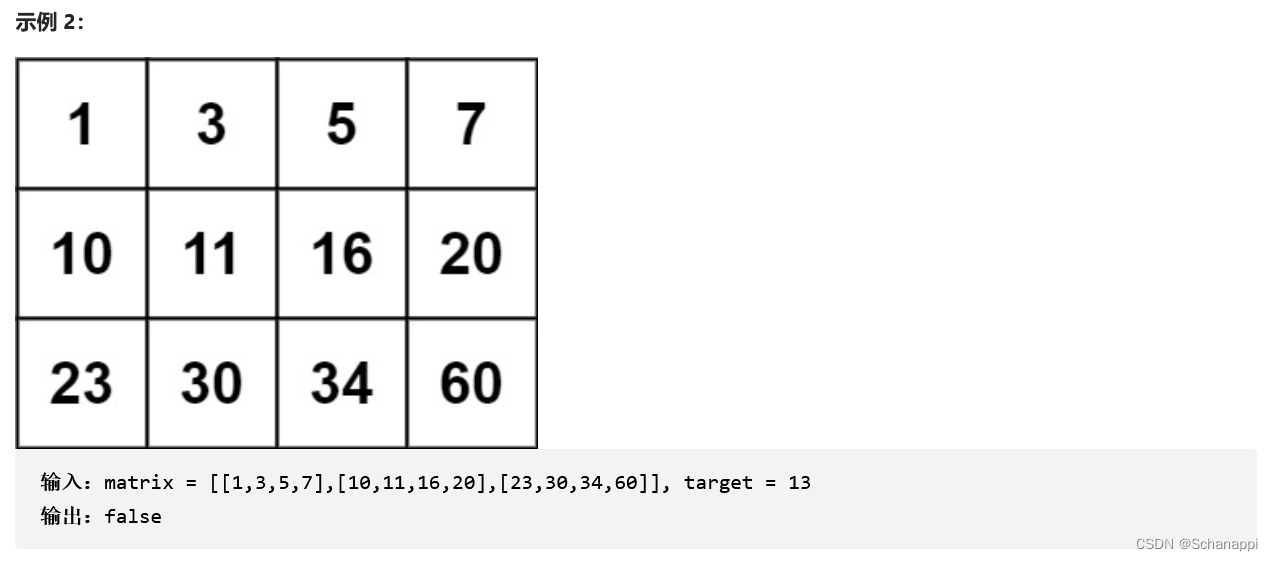

思路及代碼: 74. 搜索二維矩陣
240. 搜索二維矩陣 II(中等)


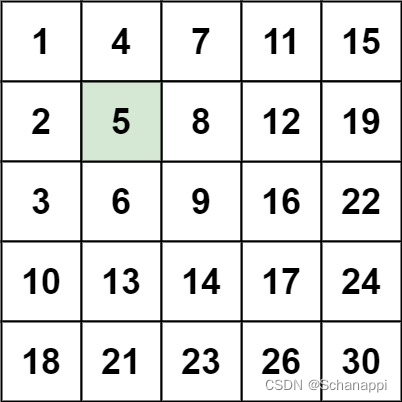

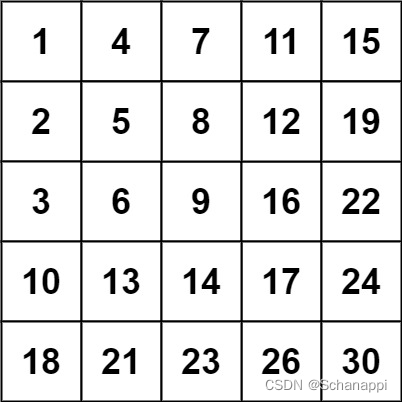


思路及代碼:240. 搜索二維矩陣 II
769. 最多能完成排序的塊(中等)


思路及代碼: 769. 最多能完成排序的塊
768. 最多能完成排序的塊 II(困難)



思路及代碼: 768. 最多能完成排序的塊 II
11.3 棧和隊列
232. 用棧實現隊列(簡單)




思路及代碼: 232. 用棧實現隊列
155. 最小棧(中等)



思路及代碼: 155. 最小棧
20. 有效的括號(簡單)



思路及代碼: 20. 有效的括號
11.4 單調棧
單調棧 通過維持棧內值的單調遞增(遞減)性,在整體 O(n) 的時間內處理需要大小比較的問題。
739. 每日溫度(中等)

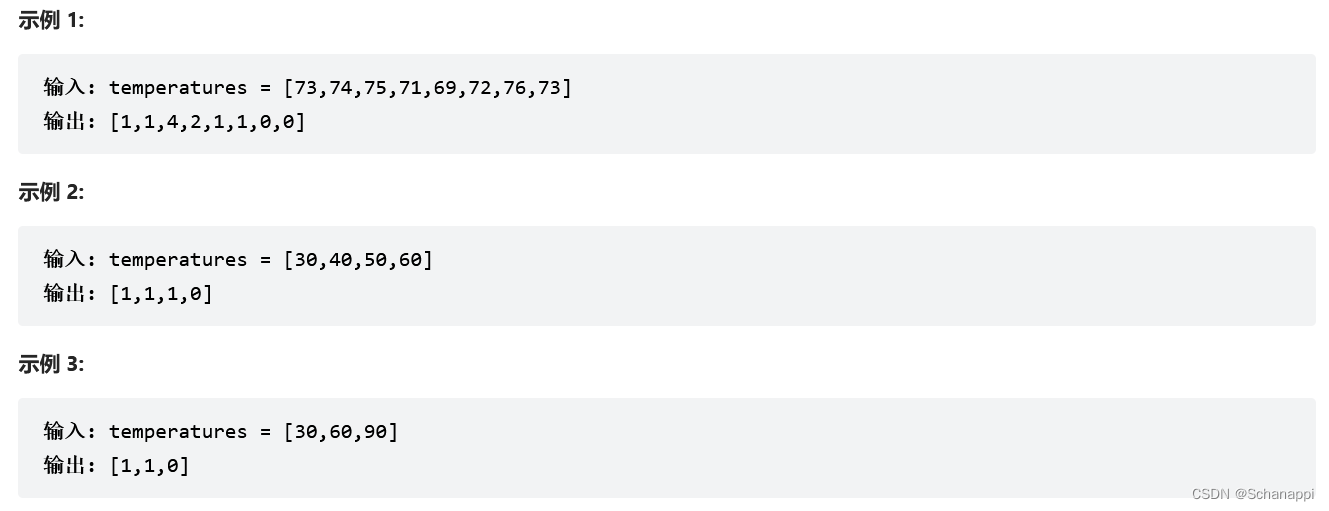

思路及代碼: 739. 每日溫度
11.5 優先隊列
-
優先隊列可以在 O(1) 時間內獲得最大值,并且可以在 O(log n) 時間內取出最大值或插入任意值。
-
優先隊列常常用 堆 來實現。堆是一個完全二叉樹,其每個節點的值總是大于等于子節點的值。實際實現堆的時候,通常用數組而不是指針建立一個樹,這是因為堆是完全二叉樹,所以用數組表示的時候,位置 i 的節點的父節點位置一定是
(i-1)/2,而它的兩個子節點的位置又一定分別為2i+1和2i+2。 -
以下是堆的實現方法,其中最核心的兩個操作是上浮和下沉:.
-
如果一個節點比父節點大,那么需要交換這兩個節點;交換后它可能比新的父節點還大,因此需要不斷進行比較和交換操作,稱之為上浮;
-
如果一個節點比父節點小,那么也需要不斷地進行向下比較和交換操作,稱之為下沉。
如果一個節點有兩個子節點,我們總是交換最大的子節點。
-
vector<int> heap;// 上浮
void swim(int pos){while(pos > 0 && heap[(pos-1)/2] < heap[pos]){swap(heap[(pos-1)/2], heap[pos]);pos = (pos - 1) / 2;}
}// 下沉
void sink(int pos){while(2 * pos + 1 <= N){int i = 2 * pos + 1;// 兩個子節點進行比較,找到更大的子節點if(i < N && heap[i] < heap[i+1]) ++i;if(heap[pos] >= heap[i]) break;swap(heap[pos], heap[i]);pos = i;}
}// 插入任意值:把新數字放到最后一位,然后上浮
void push(int k){heap.push_back(k);swim(heap.size()-1);
}// 刪除最大值:把最后一個數字挪到開頭,然后下沉
void pop(){// 原本的heap[0]就是最大值heap[0] = heap.back();heap.pop_back();sink(0);
} // 獲取最大值
int top(){return heap[0];
}
- 通過將算法中的大于號和小于號互換,我們也可以得到一個快速獲得最小值的優先隊列。
- 另外,如果在維持大小關系的同時,還需要支持查找任意值、刪除任意值、維護所有數字的大小關系等操作,可以考慮使用 set 或 map來代替優先隊列。
23. 合并 K 個升序鏈表(困難)

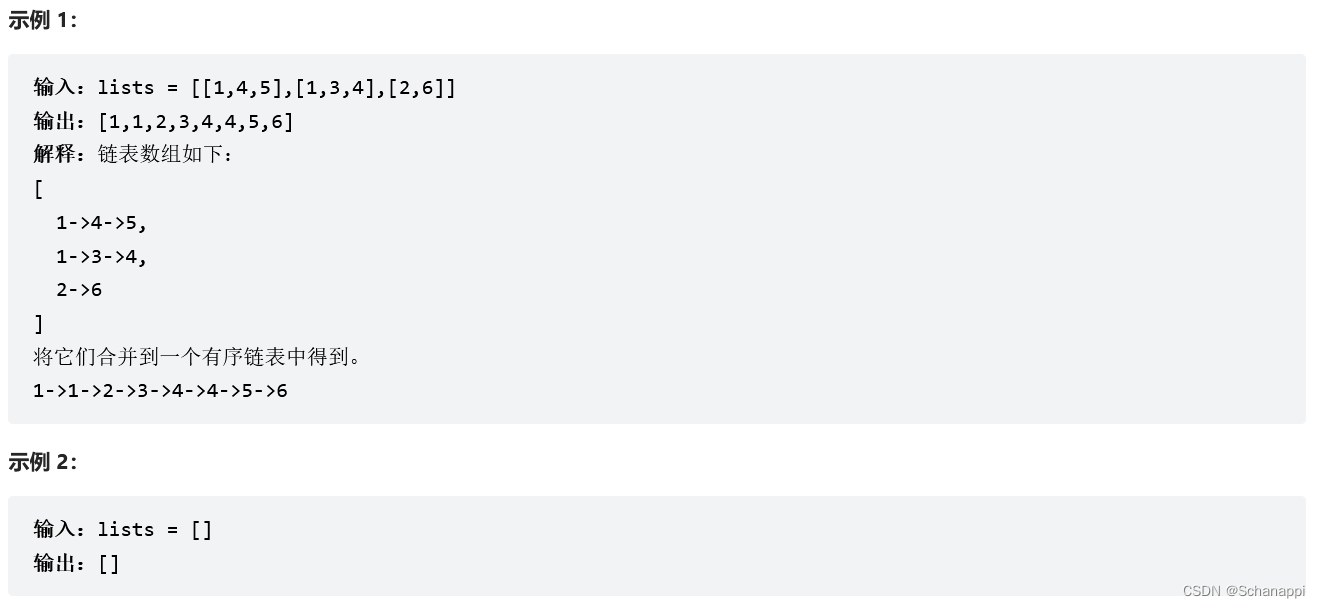


思路及代碼: 23. 合并 K 個升序鏈表
218. 天際線問題(困難)

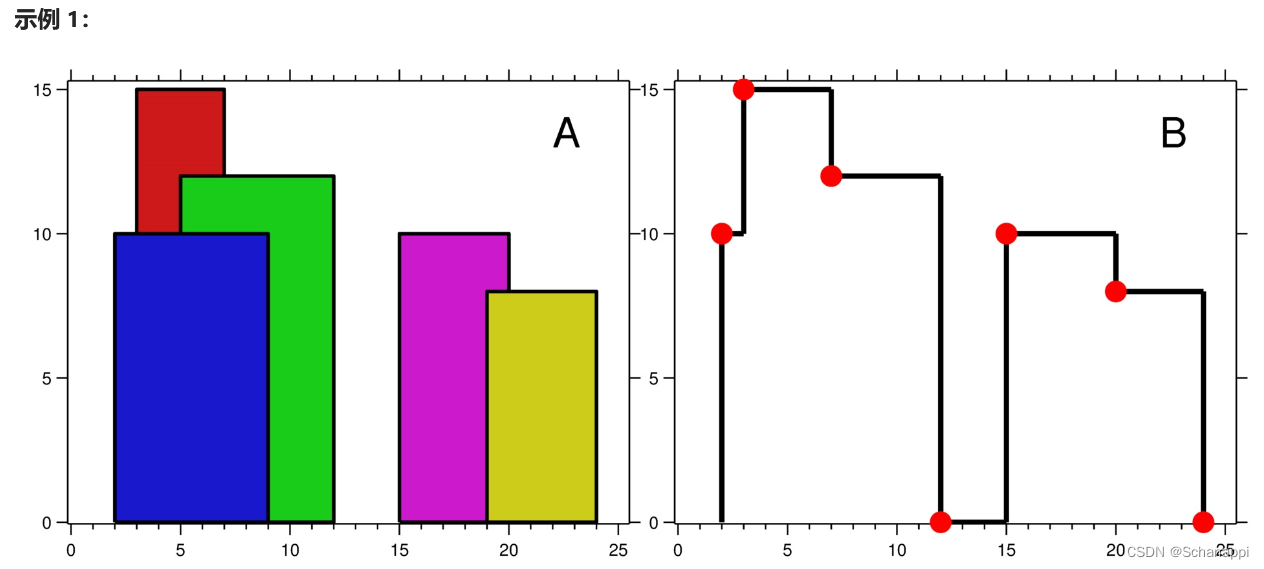


思路及代碼: 218. 天際線問題
11.6 雙端隊列
239. 滑動窗口最大值(困難)



思路及代碼: 239. 滑動窗口最大值
11.7 哈希表
- 哈希表 ,又稱散列表,使用 O(n) 空間復雜度存儲數據,通過哈希函數映射位置,從而實現近似 O(1) 時間復雜度的插入、查找和刪除操作。
- c++ 中的哈希集為 unordered_set ,可以查找元素是否在集合中,如果需要同時存儲鍵和值,則需要用 unordered_map,可以用來統計頻率,記錄內容等。如果元素有限個,并且范圍不大,則可以用一個固定大小的數組來存儲或統計元素。例如我們需要統計一個字符串中所有字母的出現次數,則可以用一個長度為 26 的數組來進行統計,其哈希函數即為字母在字母表的位置,這樣空間復雜度就可以降為常數。
1. 兩數之和(簡單)



思路及代碼: 1. 兩數之和
128. 最長連續序列(中等)



思路及代碼: 128. 最長連續序列
149. 直線上最多的點數(困難)
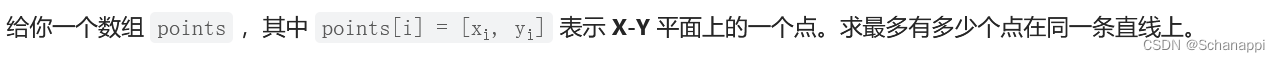
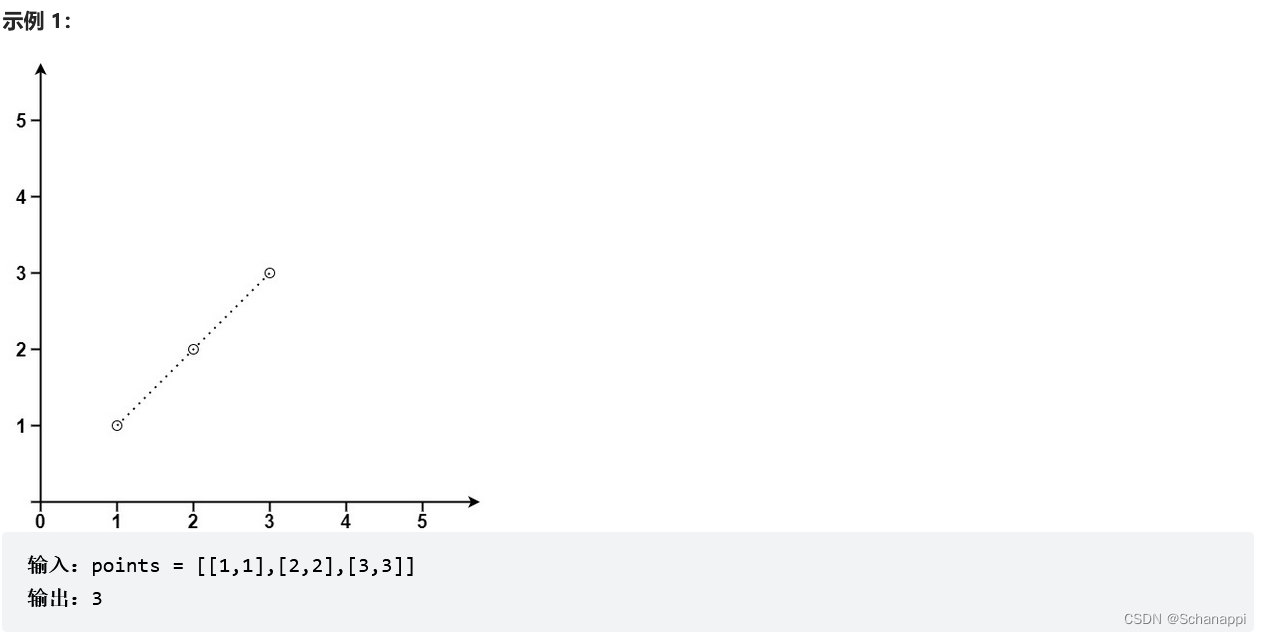
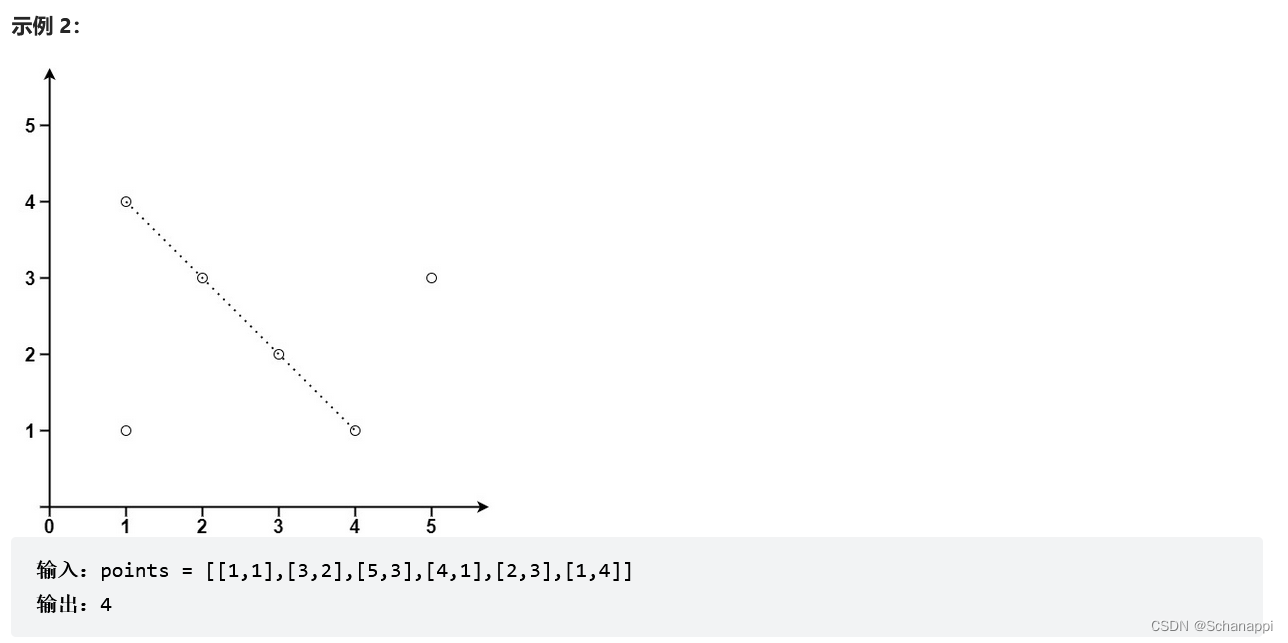

思路及代碼: 149. 直線上最多的點數
11.8 多重集合和映射
332. 重新安排行程(困難)

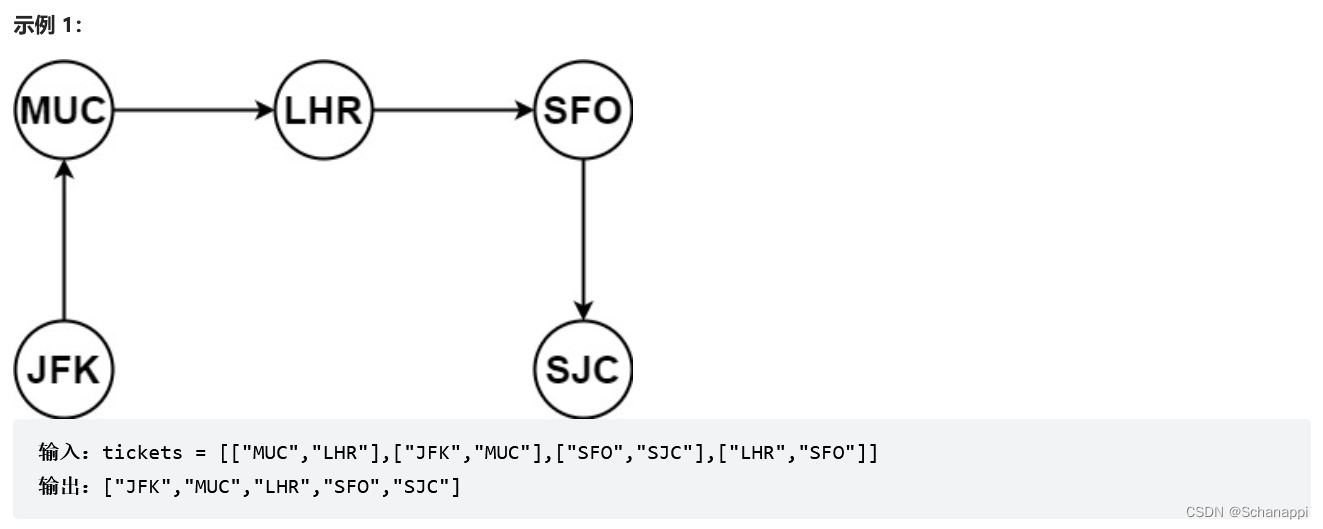


思路及代碼: 332. 重新安排行程
11.9 前綴和與積分圖
- 一維的前綴和,二維的積分圖,都是把每個位置之前的一維線段或二維矩形預先存儲,方便加速計算。如果需要對前綴和或積分圖的值做尋址,則要存在哈希表里;如果要對每個位置記錄前綴和或積分圖的值,則可以存儲到一維或二維數組里,常常伴隨著動態規劃。
303. 區域和檢索 - 數組不可變(簡單)



思路與代碼: 303. 區域和檢索 - 數組不可變
304. 二維區域和檢索 - 矩陣不可變(中等)




思路及代碼: 304. 二維區域和檢索 - 矩陣不可變
560. 和為 K 的子數組(中等)



思路及代碼: 560. 和為 K 的子數組
11.10 練習
566. 重塑矩陣(簡單)

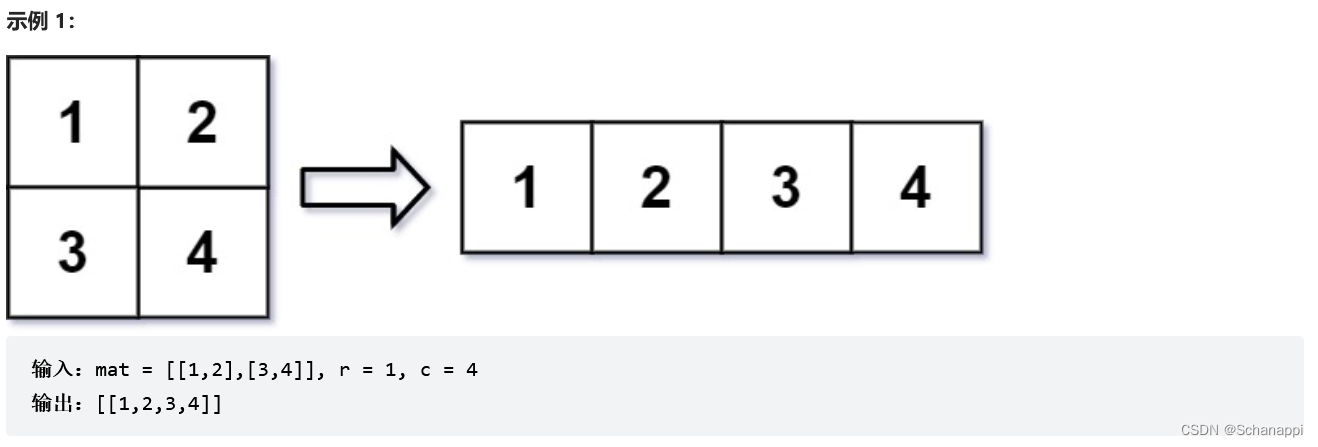
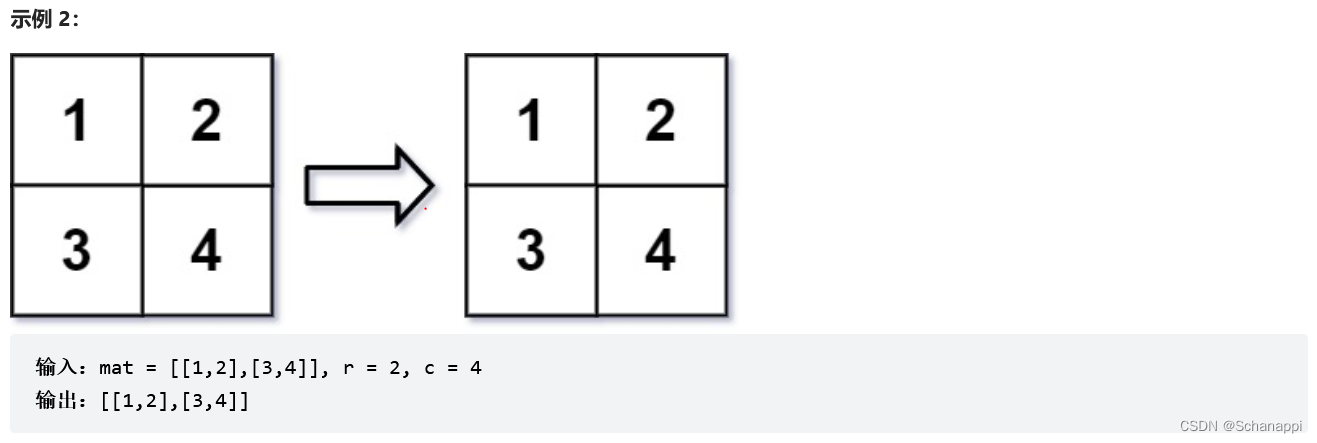

思路及代碼: 566. 重塑矩陣
225. 用隊列實現棧(簡單)



思路及代碼: 225. 用隊列實現棧
503. 下一個更大元素 II(中等)



思路及代碼: 503. 下一個更大元素 II
217. 存在重復元素(簡單)



思路及代碼: 217. 存在重復元素
697. 數組的度(簡單)



思路及代碼: 697. 數組的度
594. 最長和諧子序列(簡單)

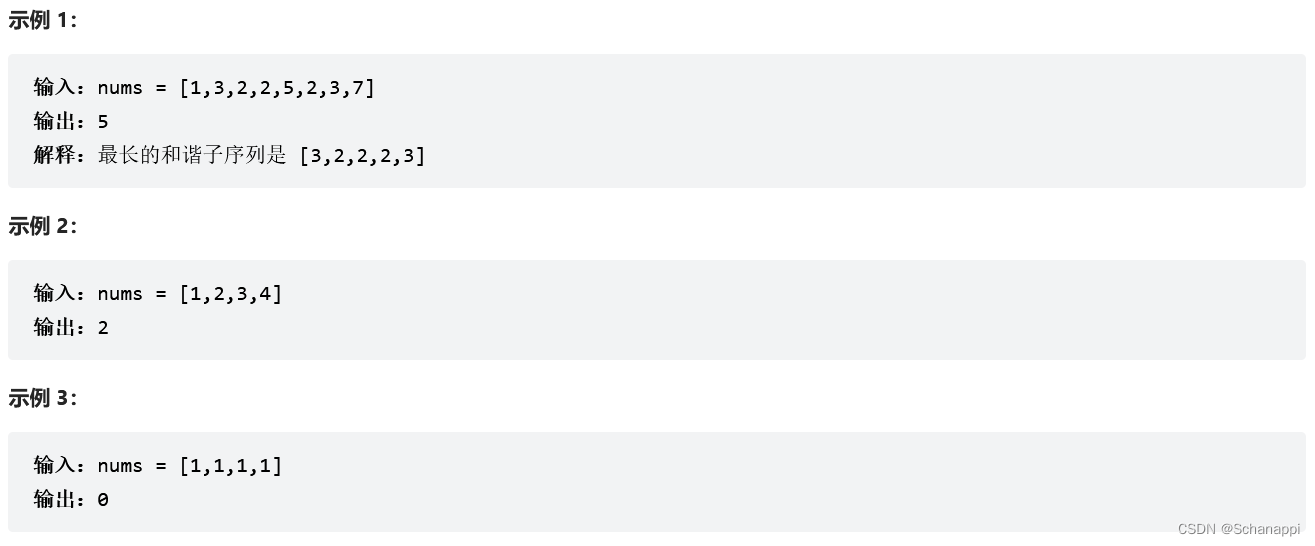

思路及代碼: 594. 最長和諧子序列
287 . 尋找重復數(中等)



思路及代碼: 287. 尋找重復數
313. 超級丑數



思路及代碼: 313. 超級丑數
870 . 優勢洗牌

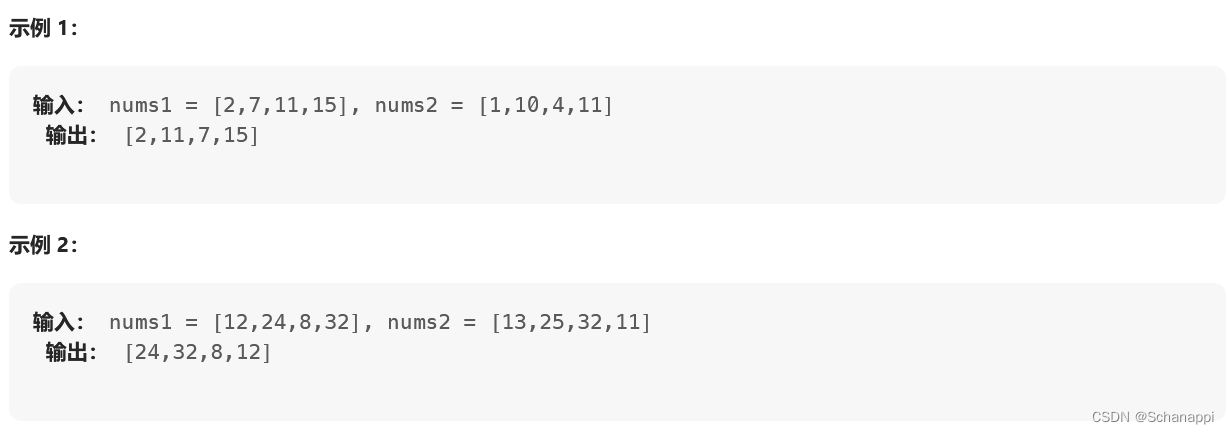

思路及代碼: 870 . 優勢洗牌
307 . 區域和檢索 - 數組可修改



思路及代碼: 307 . 區域和檢索 - 數組可修改












)
數據操作)



故障切換的運作流程原理分析(含源碼))

