在日常工作中，有一個比較常見的需求，就是需要判斷一個元素是否在集合中。

例如以下場景：

• 給定一個IP黑名單庫，檢查指定IP是否在黑名單中？

• 在接收郵件的時候，判斷一個郵箱地址是否為垃圾郵件？

• 在文字處理軟件中，檢查一個英文單詞是否拼寫正確？

遇到這種問題，通常直覺會告訴我們，應該使用集合這種數據結構來實現。例如，先將IP黑名單庫的所有IP全部存儲到一個集合中，然后再拿指定的IP到該集合中檢查是否存在，如果存在則說明該IP命中黑名單。

通過一段Java代碼，來模擬IP黑名單庫的存儲和檢查。

public class IPBlackList {

public static void main(String[] args) {
Set<String> set = new HashSet<>();
        set.add("192.168.1.1");
        set.add("192.168.1.2");
        set.add("192.168.1.4");
System.out.println(set.contains("192.168.1.1"));
System.out.println(set.contains("192.168.1.2"));
System.out.println(set.contains("192.168.1.3"));
System.out.println(set.contains("192.168.1.4"));
}

}

執行結果：

true
true
false
true

集合的內部，通常是使用散列表來實現。其優點是查詢非常高效，缺點是比較耗費存儲空間。

一般在數據量比較小的時候，我們會使用集合來進行存儲。以空間換時間，在占用空間較小的情況下，同時又能提高查詢效率。

但是，當存儲的數據量比較大的時候，耗費大量空間將會成為問題。因為這些數據通常會存儲到進程內存中，以加快查詢效率。而機器的內存通常都是有限的，要盡可能高效的使用。

另一方面，散列表在空間和效率上是需要做平衡的。存儲相同數量的元素，如果散列表容量越小，出現沖突的概率就越高，用于解決沖突的時間將會花費更多，從而影響性能。

而布隆過濾器(Bloom Filter)的產生，能夠很好的解決這個問題。一方面能夠以更少的內存來存儲數據，另一方面能夠實現非常高效的查詢性能。

布隆過濾器(Bloom Filter)

布隆過濾器(Bloom Filter)是一個數據結構，由布隆(Burton Howard Bloom)于1970年提出的。它實際上是一個很長的二進制向量和一系列隨機映射函數。

布隆過濾器可以用于高效的檢索一個元素是否在一個集合中。它的優點是空間效率和查詢時間都遠遠優于一般的算法，缺點是有一定的誤識別率，而且難以刪除(一般不支持，需要額外的實現)。

布隆過濾器之所以高效，因為它是一個概率數據結構，它能確認元素肯定不在集合中，或者元素可能在集合中。之所以說是可能，是因為它有一定的誤識別率，使得無法100%確定元素一定在集合中。

基本原理

布隆過濾器的基本工作原理并不復雜，大致如下：

首先，建立一個二進制向量，并將所有位設置為0。

然后，選定K個散列函數，用于對元素進行K次散列，計算向量的位下標。

添加元素

當添加一個元素到集合中時，通過K個散列函數分別作用于元素，生成K個值作為下標，并對向量的相應位設置為1。

檢查元素

如果要檢查一個元素是否存在集合中，用同樣的散列方法，生成K個下標，并檢查向量的相應位是否全部是1。如果全為1，則該元素很可能在集合中；否則(只要有1個或以上的位為0)，該元素肯定不在集合中。

這就是布隆過濾器的基本思想。

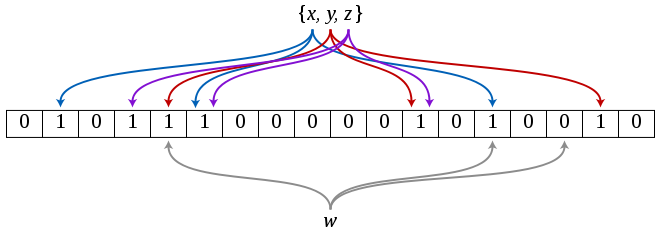
一個簡單的例子

假設有一個布隆過濾器，容量是15位，使用2個哈希函數。

添加一個字符串a，2次哈希得到下標為4和10，將4和10對應的位由0標記為1。

然后添加一個字符串b，2次哈希得到下標為11和11，將11對應的位由0標記為1。

再添加一個字符串c，2次哈希得到下標為11和12，將11和12對應的位由0標記為1。

最后，添加一個字符串sam，2次哈希得到下標為0和7，將0和7對應的位由0標記為1。

上面，我們添加了4個字符串，每個字符串分別進行2次哈希，對應的2個位標記為1，最終被標記為1的共有6位而不是8位。

這說明，不同的元素，哈希后得到的位置是可能出現重疊的。如果元素越多，出現重疊的概率會更高。如果有2個元素出現重疊的位置，我們是無法判斷任一元素一定在集合中的。

如果要檢查一下元素是否存在集合中，只需要以相同的方法，進行2次哈希，將得到的2個下標在布隆過濾器中的相應位進行查找。如果對應的2位不是全部為1，則該元素肯定不在集合中。如果對應的2位全部為1，則說明該元素可能在集合中，也可能不存在。

例如，檢查字符串b是否存在集合中，哈希得到的2個下標都為11。檢查發現，11對應的位為1。但是，這并不能說明b一定在集合中。這是因為，字符串c哈希后的下標也包含11，有可能只是字符串c在集合中，而b卻不存在，這就是造成了誤識別，也稱為假陽性。

再檢查字符串foo，哈希得到的下標分別為8和13，對應的位都為0。因此，字符串foo肯定不在集合中。

數學原理

布隆過濾器背后的數學原理是：

兩個完全隨機的數字相沖突的概率很小，因此可以在很小的誤識別率條件下，用很少的空間存儲大量信息。

解決誤識別率的2種方法

白名單

解決誤識別率的常見方法，是建立一個較小的白名單，用來存儲那些可能被誤識別的數據。

以垃圾郵件過濾為例。假設我們有一個垃圾郵件庫，用于在接收郵件的時候過濾掉垃圾郵件。

這時可以先將這個垃圾郵件庫存儲到布隆過濾器中，當接收到郵件的時候，可以先通過布隆過濾器高效的過濾出大部分正常郵件。

而對于少部分命中(可能為)垃圾郵件的，其中有一部分可能為正常郵件。

再創建一個白名單庫，當在布隆過濾器中判斷可能為垃圾郵件時，通過查詢白名單來確認是否為正常郵件。

對于沒在白名單中的郵件，默認會被移動到垃圾箱。通過人工識別的方式，當發現垃圾箱中存在正常郵件的時候，將其移入白名單。

回源確認

很多時候，使用布隆過濾器是為了低成本，高效率的攔截掉大量數據不在集合中的場景。

例如：

• Google Bigtable，Apache HBase以及Apache Cassandra和PostgreSQL 使用Bloom過濾器來減少對不存在的行或列的磁盤查找。避免進行昂貴的磁盤查找，可大大提高數據庫查詢操作的性能。

• 在谷歌瀏覽器用于使用布隆過濾器來識別惡意URL的網頁瀏覽器。首先會針對本地Bloom過濾器檢查所有URL，只有在Bloom過濾器返回肯定結果的情況下，才對執行的URL進行全面檢查(如果該結果也返回肯定結果，則用戶會發出警告)。

• 攔截掉大量非IP黑名單請求，對于少量可能在黑名單中的IP，再查詢一次黑名單庫。

這是布隆過濾器非常典型的應用場景，先過濾掉大部分請求，然后只處理少量不明確的請求。

這個方法，和白名單庫的區別是，不需要再另外建立一套庫來處理，而是使用本來就已經存在的數據和邏輯。

例如Google Bigtable查詢數據行本來就是需要查的，只不過使用布隆過濾器攔截掉了大部分不必要的請求。而IP是否為黑名單也是需要查詢的，同樣是先使用布隆過濾器來攔截掉大部分IP。

而上面垃圾郵件的處理，對于可能為垃圾郵件的情況，不是通過完整的垃圾郵件庫再查詢一次進行確認，而是用增加白名單來進行判斷的方式。因為通常來說，白名單庫會更小，便于緩存。

這里所說的回源，實際上是對可能被誤識別的請求，最后要回到數據源頭或邏輯確認一次。

參考

https://en.wikipedia.org/wiki/Bloom_filter

https://en.wikipedia.org/wiki/Bloom_filter

https://zh.wikipedia.org/zh-cn/布隆過濾器

https://llimllib.github.io/bloomfilter-tutorial

https://www.geeksforgeeks.org/bloom-filter-in-java-with-examples/

《數學之美》

---

題圖：wikipedia.org極客教程：996geek.com個人博客：binarylife.icu