?
目錄
樹?
樹的學術名詞
樹的種類
?二叉樹的遍歷
算法實現
遍歷命名
二叉樹的中序遍歷
二叉樹的后序遍歷
二叉樹的后序遍歷迭代算法
?二叉樹的前序遍歷
二叉樹的前序遍歷迭代算法
?

樹?
樹是一種非線性的數據結構,它是由n(n≥0)個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。它具有以下的特點:
- 每個節點有零個或多個子節點;
- 沒有父節點的節點稱為根節點;
- 每一個非根節點有且只有一個父節點;
- 除了根節點外,每個子節點可以分為多個不相交的子樹
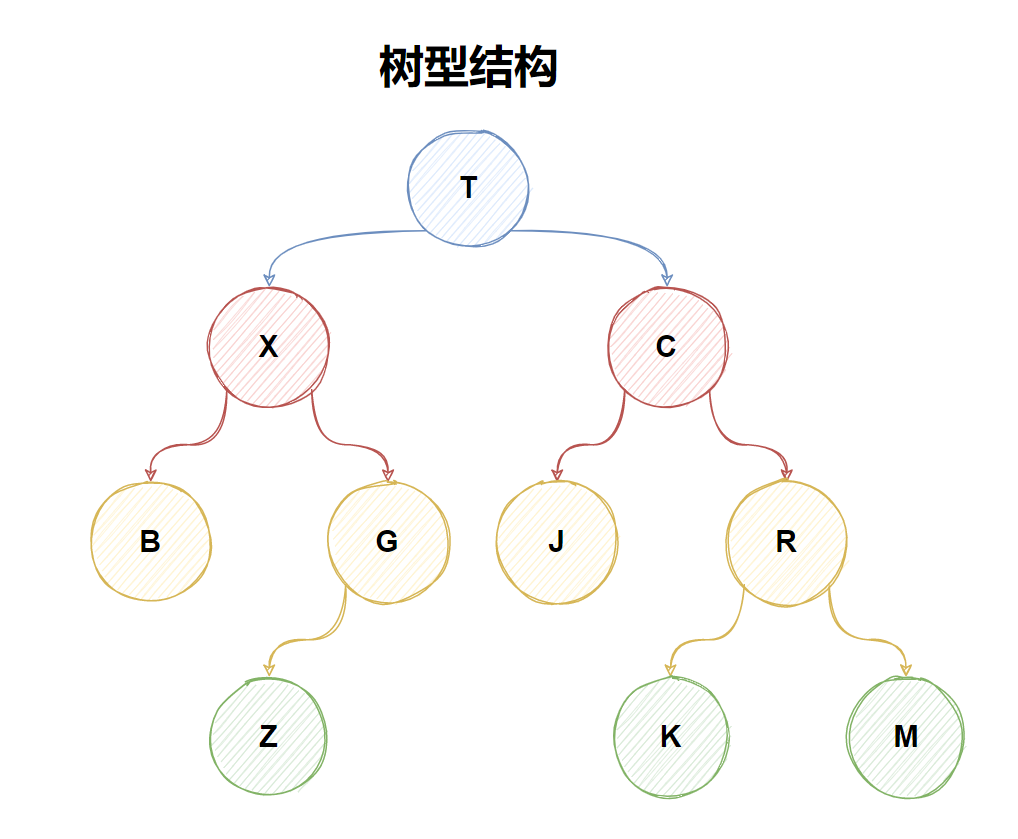
樹的學術名詞
- 根節點(root): 樹的最上層的節點,任何非空的樹都有一個節點
- 路徑(path): 從起始節點到終止節點經歷過的邊
- 父親(parent):除了根節點,每個節點的上一層邊連接的節點就是它的父親(節點)
- 孩子(children): 每個節點由邊指向的下一層節點
- 兄弟(siblings): 同一個父親并且處在同一層的節點
- 子樹(subtree): 每個節點包含它所有的后代組成的子樹
- 葉子節點(leaf node): 沒有孩子的節點成為葉子節點
樹的種類
無序樹:樹中任意節點的子結點之間沒有順序關系,這種樹稱為無序樹,也稱為自由樹;
有序樹:樹中任意節點的子結點之間有順序關系,這種樹稱為有序樹;
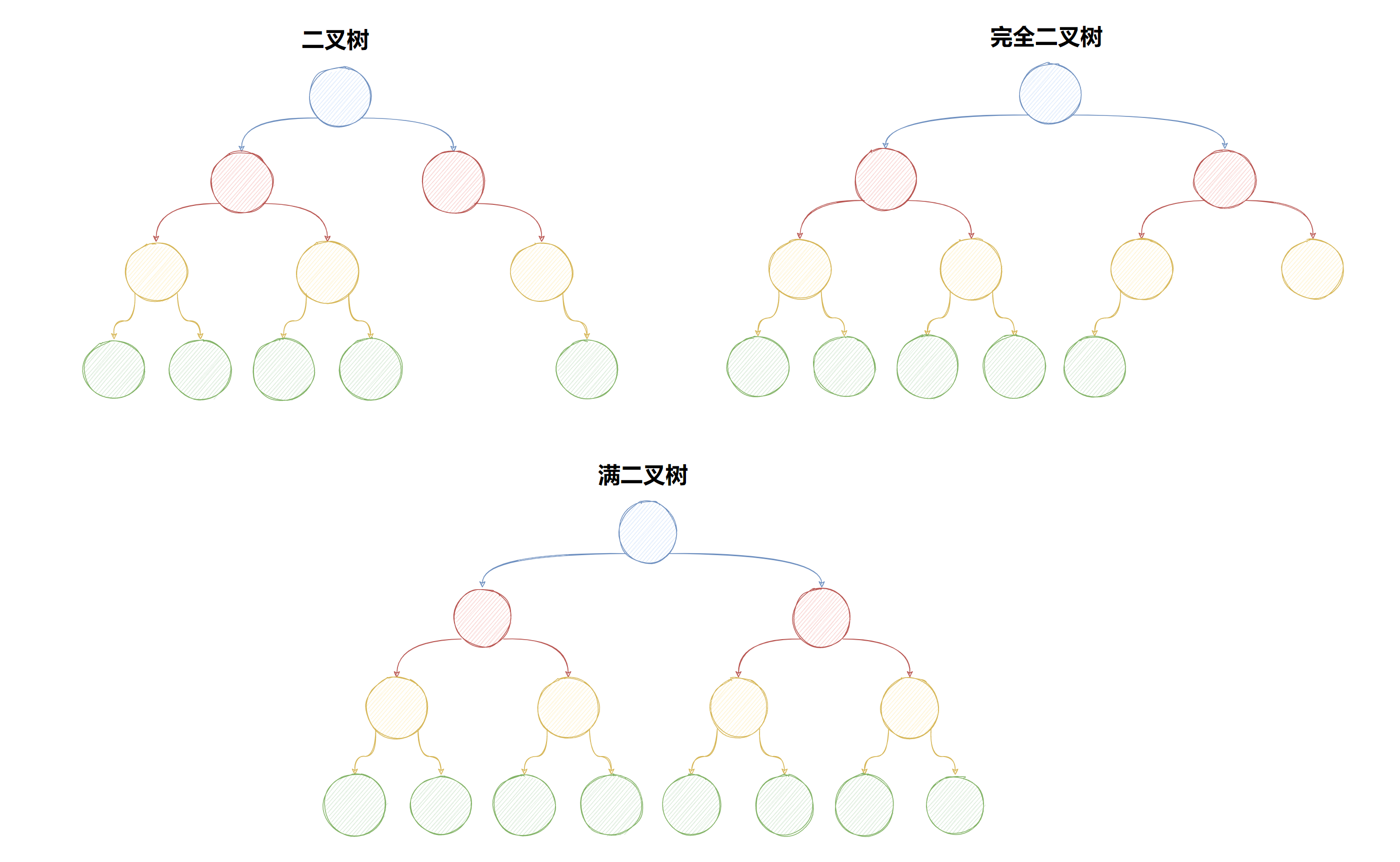
二叉樹:每個節點最多含有兩個子樹的樹稱為二叉樹;
滿二叉樹:所有節點均含有兩個子樹的樹被稱為滿二叉樹;
完全二叉樹:除最后一層外,所有層都是滿節點,且最后一層缺右邊連續節點的二叉樹稱為完全二叉樹;
哈夫曼樹(最優二叉樹):帶權路徑最短的二叉樹稱為哈夫曼樹或最優二叉樹。
?二叉樹的遍歷
所謂遍歷(Traversal)是指沿著某條搜索路線,依次對樹中每個結點均做一次且僅做一次訪問
訪問結點所做的操作依賴于具體的應用問題。 遍歷是二叉樹上最重要的運算之一,是二叉樹上進行其它運算之基礎
算法實現
從二叉樹的遞歸定義可知,一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此,在任一給定結點上,可以按某種次序執行三個操作:
- 訪問節點的本身(Node)
- 遍歷該節點的左子樹(L)
- 遍歷該節點的右子樹 (R)
以上三種操作擁有六種執行順序:
NLR,LNR,LRN,NRL,RNL,RLN。
但是注意前三種次序和后三種次序對稱,所以我們只學習前三種次序
遍歷命名
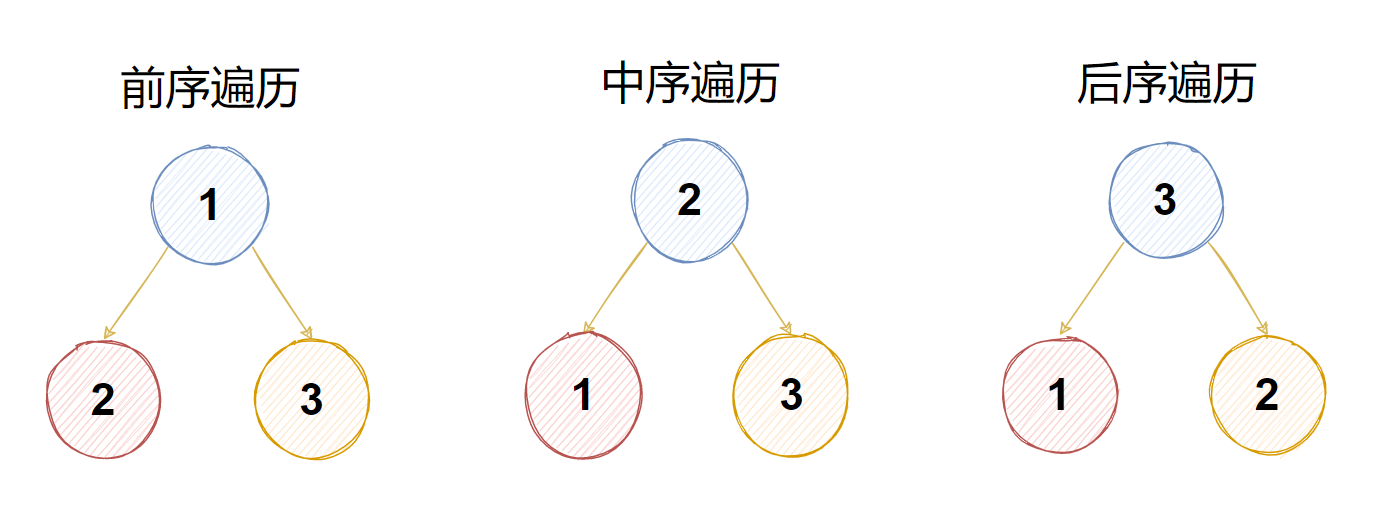
根據訪問結點操作發生位置命名:
-
NLR:二叉樹的前序遍歷(Preorder Traversal 亦稱(先序遍歷))
訪問根結點的操作發生在遍歷其左右子樹之前
-
LNR:二叉樹的中序遍歷(Inorder Traversal)
訪問根結點的操作發生在遍歷其左右子樹之中(間)
-
LRN:二叉樹的后序遍歷(Postorder Traversal)
訪問根結點的操作發生在遍歷其左右子樹之后
?
二叉樹的中序遍歷
若二叉樹非空,則依次執行如下操作:
- 遍歷左子樹
- 訪問根節點
- 遍歷右子樹

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:# 左 根 右def inorder(root : TreeNode):if not root:returninorder(root.left)res.append(root.val)inorder(root.right)res = list()inorder(root)return res
?
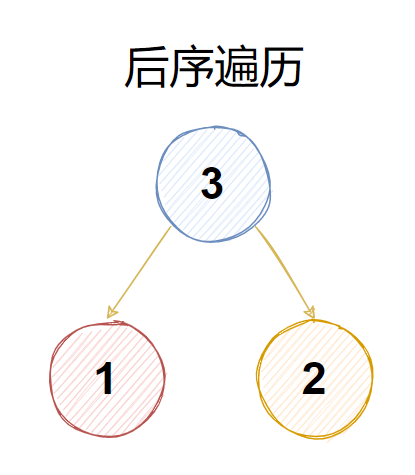
二叉樹的后序遍歷
若二叉樹非空,則依次執行如下操作:
- 遍歷左子樹
- 遍歷右子樹
- 訪問根節點
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:# 后序遍歷的順序:左 右 根def postorder(root : TreeNode):if not root:returnpostorder(root.left)postorder(root.right)res.append(root.val)res = list()postorder(root)return res
二叉樹的后序遍歷迭代算法
-
建立一個棧,用來存儲節點。
-
根據根右左的順序將節點依次壓入棧中,在壓入棧中的同時,按照順序把節點里的元素依次壓入棧中。輸出完畢之后按照順序彈棧。
-
將答案數組進行反轉,得到左右根順序的數組
-
輸出答案
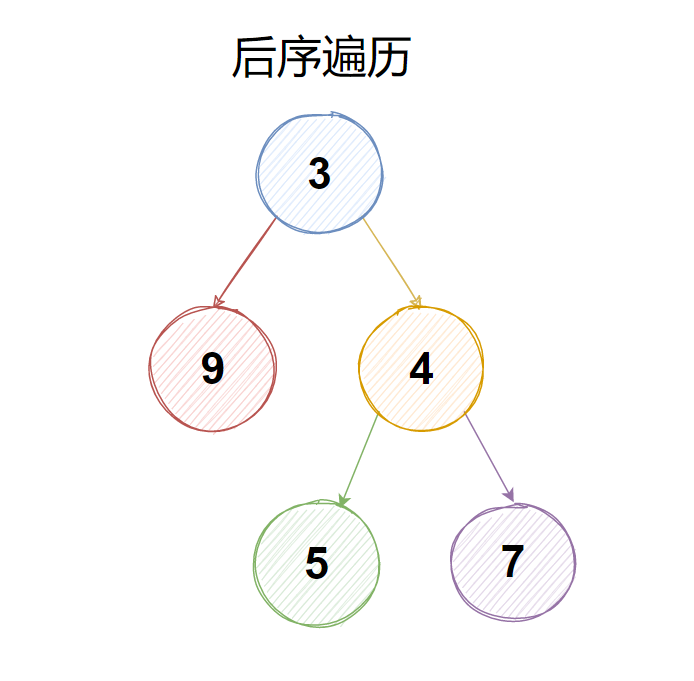
期望結果:[9,5,7,4,3]
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:res = []stack = []while root or stack:while root:res.append(root.val)stack.append(root)root = root.rightroot = stack.pop().left #根 右 左的順序res.reverse() return res
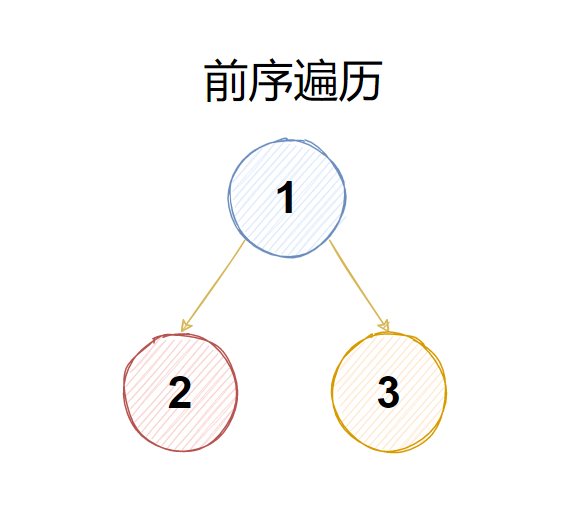
?二叉樹的前序遍歷
若二叉樹非空,則依次執行如下操作:
-
訪問根節點
-
遍歷左子樹
-
遍歷右子樹
?
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:# 創建一個集合存儲數據res = []def preorder(root:TreeNode):# 判斷root是否有值if not root:returnelse:# 獲取根節點res.append(root.val)# 獲取左節點preorder(root.left)# 獲取右節點preorder(root.right)preorder(root)return res二叉樹的前序遍歷迭代算法
- 建立一個棧,用來存儲節點。
- 根據左右根的順序將節點依次壓入棧中,在壓入棧中的同時,按照順序把節點里的元素依次壓入棧中。輸出完畢之后按照順序彈棧。
- 輸出答案。
class Solution:def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:# 創建res存儲結果res = []stack = [] # 存儲分支節點# 只要root有數據 或者stack的數據while root or stack:# 只要root有數據,第一輪循環把左節點搞定while root:res.append(root.val)stack.append(root)# 獲取左節點root = root.left# 取出右節點,遍歷root = stack.pop().rightreturn res
?
?
?
?
?
?

【前后端不分離】自定義View)

















