文章目錄
- 題目
- 標題和出處
- 難度
- 題目描述
- 要求
- 示例
- 數據范圍
- 解法
- 思路和算法
- 代碼
- 復雜度分析
題目
標題和出處
標題:二叉樹的直徑
出處:543. 二叉樹的直徑
難度
3 級
題目描述
要求
給定二叉樹的根結點 root \texttt{root} root,返回其直徑長度。
二叉樹的直徑是任意兩個結點之間的最長路徑長度。這條路徑可能穿過也可能不穿過根結點。
兩個結點之間的路徑長度由它們之間邊的數目表示。
示例
示例 1:
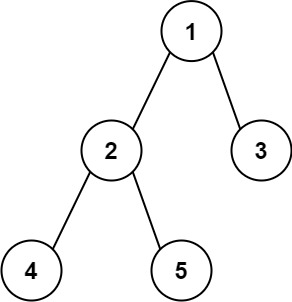
輸入: root = [1,2,3,4,5] \texttt{root = [1,2,3,4,5]} root?=?[1,2,3,4,5]
輸出: 3 \texttt{3} 3
解釋: 3 \texttt{3} 3 是路徑 [4,2,1,3] \texttt{[4,2,1,3]} [4,2,1,3] 或 [5,2,1,3] \texttt{[5,2,1,3]} [5,2,1,3] 的長度。
示例 2:
輸入: root = [1,2] \texttt{root = [1,2]} root?=?[1,2]
輸出: 1 \texttt{1} 1
數據范圍
- 樹中結點數目在范圍 [1, 10 4 ] \texttt{[1, 10}^\texttt{4}\texttt{]} [1,?104] 內
- -100 ≤ Node.val ≤ 100 \texttt{-100} \le \texttt{Node.val} \le \texttt{100} -100≤Node.val≤100
解法
思路和算法
二叉樹中的任意一條路徑一定經過某個子樹的根結點,子樹可以是二叉樹本身。
對于任意一個子樹而言,經過該子樹根結點的最長路徑(以下稱為「最長路徑」,均指包含根結點的最長路徑)一定滿足以下條件:如果左子樹不為空,則最長路徑的左端是左子樹的最深葉結點,否則最長路徑的左端是根結點;如果右子樹不為空,則最長路徑的右端是右子樹的最深葉結點,否則最長路徑的右端是根結點。因此,子樹的最長路徑長度為該子樹的左子樹和右子樹的深度之和,子樹的深度為該子樹的左子樹和右子樹的深度的較大值加 1 1 1。此處的深度定義為二叉樹中結點的層數,如果二叉樹為空則深度為 0 0 0,如果二叉樹只有一個結點則深度為 1 1 1。
由于二叉樹的最長路徑長度和二叉樹的深度都取決于左子樹和右子樹的深度,因此可以使用深度優先搜索計算二叉樹的深度,計算過程中得到二叉樹的直徑。
計算二叉樹的深度的過程是一個遞歸的過程,遞歸的終止條件是當前結點為空,此時深度為 0 0 0。其余情況下,首先得到當前結點的左子樹和右子樹的深度,然后計算以當前結點為根結點的二叉樹的深度和最長路徑長度,并維護二叉樹的直徑。遍歷結束之后,即可得到二叉樹的直徑。
代碼
class Solution {int diameter = 0;public int diameterOfBinaryTree(TreeNode root) {getDepth(root);return diameter;}public int getDepth(TreeNode node) {if (node == null) {return 0;}int leftDepth = getDepth(node.left);int rightDepth = getDepth(node.right);diameter = Math.max(diameter, leftDepth + rightDepth);return Math.max(leftDepth, rightDepth) + 1;}
}
復雜度分析
-
時間復雜度: O ( n ) O(n) O(n),其中 n n n 是二叉樹的結點數。每個結點都被訪問一次。
-
空間復雜度: O ( n ) O(n) O(n),其中 n n n 是二叉樹的結點數。空間復雜度主要是遞歸調用的棧空間,取決于二叉樹的高度,最壞情況下是 O ( n ) O(n) O(n)。



------ beginWork的工作流程【mount】)





)
![[C語言] 指針](http://pic.xiahunao.cn/[C語言] 指針)








前后端對接)